Page affichée à 01:23:44 vendredi 01 décembre 2023 Ce site n'utilise pas de cookie.		Dôme acoustique	Compteur pour tout le site : 13 304 517 Nombre actuel de lecteurs : 52.
		Le site de Dominique, un amateur passionné

• 1 : Technique, PC hi-fi, mesure, câbles
  • 1-1 : Notions techniques
    • 1-1-1 : L'auditeur
      • 1-1-1-1 : La haute fidélité
      • 1-1-1-2 : Les audiophiles
      • 1-1-1-3 : Philosophie audiophile
      • 1-1-1-4 : Ambition, potentiel et résultats à l'écoute
      • 1-1-1-5 : Le nécessaire et l'accessoire
      • 1-1-1-6 : Vrais problèmes, bonnes et moins bonnes solutions
      • 1-1-1-7 : Mon audition a changé
    • 1-1-2 : Théorie sur les haut-parleurs
      • 1-1-2-1 : haut-parleurs, aspects théoriques
      • 1-1-2-2 : Grave, médium et aigu
      • 1-1-2-3 : Le grave
      • 1-1-2-4 : Grave rapide
      • 1-1-2-5 : La masse de la membrane d'un haut-parleur de
        graves est-elle un ennemi de sa réponse transitoire ?
      • 1-1-2-6 : La dynamique en Hi-Fi
      • 1-1-2-7 : Masse mécanique de rayonnement arrière
      • 1-1-2-8 : SPL théorique d'un haut-parleur
      • 1-1-2-9 : Célérité de l'air, C et Ro
      • 1-1-2-10 : Champ libre
      • 1-1-2-11 : Comprendre facilement le groupe délai
      • 1-1-2-12 : Octave et calculs associés
    • 1-1-3 : Caractéristiques des haut-parleurs
      • 1-1-3-1 : Des données haut-parleur juste
      • 1-1-3-2 : Directivité des haut-parleurs
      • 1-1-3-3 : Les non-linéarités
      • 1-1-3-4 : Les transitoires
      • 1-1-3-5 : Schéma électrique équivalent à un haut-parleur
      • 1-1-3-6 : Calculs avec plusieurs haut-parleurs
      • 1-1-3-7 : Calculs en base de données, paramètres T&S
    • 1-1-4 : La phase acoustique
      • 1-1-4-1 : Menu global sur la phase acoustique
      • 1-1-4-2 : La phase acoustique
      • 1-1-4-3 : La correction numérique les monitors
        de studio NEUMANN et HEDD
      • 1-1-4-4 : La mise en phase des haut-parleurs
      • 1-1-4-5 : Mesure de la phase acoustique d'une enceinte
      • 1-1-4-6 : Filtre passe tout
      • 1-1-4-7 : Phase et temps de propagation de groupe
        d'un filtre
    • 1-1-5 : Correction des HP montés dans leur enceinte
      • 1-1-5-1 : Ma courbe cible
      • 1-1-5-2 : Baffle step : Correction de la taille
        de la face avant de l'enceinte
      • 1-1-5-3 : Égaliseur et égalisation
      • 1-1-5-4 : Limiter la courbe de réponse d'une enceinte
      • 1-1-5-5 : Courbe ISO 2969X
      • 1-1-5-6 : Loi des 400 000
      • 1-1-5-7 : Absorption atmosphérique
      • 1-1-5-8 : Influence du local sur les enceintes acoustiques
      • 1-1-5-9 : La grosse caisse et la guitare basse en Hi-Fi sous 125 Hz
    • 1-1-6 : Impédance et branchement
      • 1-1-6-1 : Impédance d'une enceinte
    • 1-1-7 : Commerce
      • 1-1-7-1 : Enceintes et amplis du commerce
      • 1-1-7-2 : Bêtisier
      • 1-1-7-3 : Puissance minimale de l'ampli
      • 1-1-7-4 : Les lecteurs CD
      • 1-1-7-5 : Le haut de gamme, revues Hi-Fi et salons
    • 1-1-8 : Divers
      • 1-1-8-1 : Réparation des HP
      • 1-1-8-2 : Placement optimal des enceintes
        dans votre pièce d'écoute
      • 1-1-8-3 : Orientation des enceintes
        par rapport au point d'écoute
      • 1-1-8-4 : Hi-Fi et vidéo sur les forums
      • 1-1-8-5 : Écoute des autres systèmes
      • 1-1-8-6 : Je débute : Le cahier des charges de vos enceintes
      • 1-1-8-7 : La Hi-Fi pour les débutants
      • 1-1-8-8 : Le son 3D à partir d’un Signal Stéréo
    • 1-1-9 : Livres
      • 1-1-9-1 : Les livres
      • 1-1-9-2 : Les composants passifs, leurs influences
        sur le son
      • 1-1-9-3 : Une enceinte donnée, un HP unique
      • 1-1-9-4 : L'enceinte PHONOPHONE BG
      • 1-1-9-5 : Table des matières, les haut-parleurs
        par G.A. BRIGGS en 1962
      • 1-1-9-6 : Table des matières, Reproduction sonore
        à haute-fidélité par G.A. BRIGGS en 1958
  • 1-2 : PC et Hi-Fi, corrections par convolution
    • 1-2-1 : Philosophie et méthodes applicables à la convolution
      • 1-2-1-1 : Philosophie audiophile
      • 1-2-1-2 : Philosophie sur la distance de mesure
      • 1-2-1-3 : La phase acoustique
      • 1-2-1-4 : Pourquoi faut-il corriger ?
      • 1-2-1-5 : Corrections par convolution de vos enceintes acoustiques
      • 1-2-1-6 : Plan d'expérience sur les corrections par convolution
      • 1-2-1-7 : Ma courbe cible
      • 1-2-1-8 : La transformée de Linkwitz
      • 1-2-1-9 : Limiter la courbe de réponse d'une enceinte
      • 1-2-1-10 : Mesure de la phase acoustique
    • 1-2-2 : Dématérialisation et égalisation
      • 1-2-2-1 : Le B A BA de la musique dématérialisée
      • 1-2-2-2 : PC et Hi-Fi
      • 1-2-2-3 : PC juke-box
      • 1-2-2-4 : PC multiroom
      • 1-2-2-5 : PC radio
      • 1-2-2-6 : Correction de la phase acoustique
      • 1-2-2-7 : Filtrage
      • 1-2-2-8 : Synoptique de 5 configurations
      • 1-2-2-9 : La touche mono numérique
      • 1-2-2-10 : Réduire la stéréo
    • 1-2-3 : Les briques de base
      • 1-2-3-1 : Foobar, Resampleur SoX, Convolver
      • 1-2-3-2 : JRiver
      • 1-2-3-3 : rePhase
      • 1-2-3-4 : Que faut-il corriger ?
      • 1-2-3-5 : Correction sans mesure
      • 1-2-3-6 : Audacity
      • 1-2-3-7 : VSTHost et Convolver VST
      • 1-2-3-8 : Correction par convolution multisource
      • 1-2-3-9 : Exact Audio Copy et le format flac
      • 1-2-3-10 : L'upsampling
      • 1-2-3-11 : Piloter Foobar avec une tablette
      • 1-2-3-12 : Par quoi remplacer un mini DSP ?
      • 1-2-3-13 : Dante
    • 1-2-4 : De l'aide pour vos corrections par convolution
  • 1-3 : La mesure
    • 1-3-1 : Matériel de mesure
      • 1-3-1-1 : Pourquoi faut-il s'équiper d'un système de mesure ?
      • 1-3-1-2 : Matériel pour la mesure d'un HP ou d'une enceinte
      • 1-3-1-3 : Mesures dans les revues
      • 1-3-1-4 : Mesures et mise au point : Contexte et méthode
    • 1-3-2 : Mesures d'impédance
      • 1-3-2-1 : Mesure de Fs, Re, Qms, Qes, Qts et Sd
      • 1-3-2-2 : Mesure de Mms, Vas et BL
      • 1-3-2-3 : Formulaire de calcul des paramètres mesurés, 1/5
      • 1-3-2-4 : Mesure spécifique pour un tweeter
      • 1-3-2-5 : Moyenne des paramètres T&S
    • 1-3-3 : Mesures avec un micro
      • 1-3-3-1 : Mesure courbe de réponse
        en bruit rose
      • 1-3-3-2 : Mesure MMM au point d'écoute
        en bruit rose
      • 1-3-3-3 : Mesure de la phase acoustique
        et de la réponse, en sweep
      • 1-3-3-4 : Garder la partie utile de l'impulsion
      • 1-3-3-5 : Traiter dans Excel le multifenêtrage
      • 1-3-3-6 : Réglage des délais entre les HP
      • 1-3-3-7 : Les effets du sol pendant la mesure
      • 1-3-3-8 : Mesure de la distorsion d'une enceinte
    • 1-3-4 : Mesures au banc Klippel
      • 1-3-4-1 : Distorsion et bass-reflex
  • 1-4 : Les câbles
    • 1-4-1 : Qu'est-ce qu'un câble ?
      • 1-4-1-1 : Préambule
      • 1-4-1-2 : Qu'est-ce qu'un câble ?
      • 1-4-1-3 : Une approche câble différente
    • 1-4-2 : Les boucles de masse
      • 1-4-2-1 : Bourdonnements, ronflettes et autres bzzzz
      • 1-4-2-2 : La prise de terre de nos appareils hi-fi
      • 1-4-2-3 : Terre, masse et boucle de masse
      • 1-4-2-4 : Diagnostic de votre installation
      • 1-4-2-5 : Les solutions
      • 1-4-2-6 : Réduire la taille des boucles de masse
      • 1-4-2-7 : Le câblage des studios d'enregistrement
    • 1-4-3 : Les câbles de liaison
      • 1-4-3-1 : Les câbles de modulation RCA et XLR
      • 1-4-3-2 : Les câbles pour liaison numérique
      • 1-4-3-3 : Les câbles pour liaison HP
      • 1-4-3-4 : Branchements ampli vers HP, bicâblage
      • 1-4-3-5 : Les câbles secteur
      • 1-4-3-6 : Câble HDMI
      • 1-4-3-7 : Essais à l'écoute sur les câbles
      • 1-4-3-8 : La connectique
      • 1-4-3-9 : La soudure
  • 1-5 : Autour des HP et enceintes
    • 1-5-1 : Détails et solutions
      • 1-5-1-1 : Les détails qui changent tout
      • 1-5-1-2 : Les solutions qui marchent
    • 1-5-2 : Les antennes FM et UHT
      • 1-5-2-1 : L'antenne FM
      • 1-5-2-2 : Les antennes UHF pour TNT
    • 1-5-3 : Les résonateurs
      • 1-5-3-1 : Résonateur de HELMHOLTZ
      • 1-5-3-2 : Résonateur dynharmonique
    • 1-5-4 : Platine vinyle
      • 1-5-4-1 : Gabarit de réglage bras et cellule
    • 1-5-5 : Branchement d'un haut-parleur sur un ampli à tubes
      • 1-5-5-1 : Branchement d'un haut-parleur sur un ampli à tubes
  • 1-6 : Acoustique des pièces et studios
    • 1-6-1 : Le traitement acoustique d'un studio
      d'enregistrement
    • 1-6-2 : Plusieurs approches distinctes
      pour le traitement acoustique en studio
    • 1-6-3 : Liens traitements acoustiques
    • 1-6-4 : Annuler l'influence de la pièce
      dans les graves
• 2 : Baffles, enceintes, calculs, réalisations, HC
  • 2-1 : Enceintes fermées
    • 2-1-1 : Les enceintes à évent, bass-reflex
      • 2-1-1-1 : Calcul d'une enceinte bass-reflex
      • 2-1-1-2 : Les limites des conseils
      • 2-1-1-3 : Faut-il bannir les enceintes à évent ?
      • 2-1-1-4 : Domaine d'utilisation d'un haut-parleur
      • 2-1-1-5 : Annuler l'influence de la pièce
        dans les graves
      • 2-1-1-6 : Calcul d'évent
      • 2-1-1-7 : Forme de l'évent
      • 2-1-1-8 : Résistance en série
      • 2-1-1-9 : Simulation et limite
      • 2-1-1-10 : Élongation et puissance
      • 2-1-1-11 : Comprendre facilement le groupe délai
      • 2-1-1-12 : Bass-reflex de très grand volume
      • 2-1-1-13 : L'optimisation par le rendement
    • 2-1-2 : Les enceintes à évent à triple résonateur
      • 2-1-2-1 : Calculs d'une enceinte à triple résonateur
      • 2-1-2-2 : Double et triple résonateur
      • 2-1-2-3 : Le filtre de Briggs
      • 2-1-2-4 : Gamme Elipson en 1975 et résonateur
      • 2-1-2-5 : Résonateur Elipson
      • 2-1-2-6 : Réparation Elipson 1303 X
    • 2-1-3 : Calcul des enceintes à évent
      • 2-1-3-1 : Explication des recherches multicritères
        Exemple avec une enceinte à évent
      • 2-1-3-2 : Recherche multicritères des HP
        pour enceinte à évent
      • 2-1-3-3 : Recherche multicritères BESSEL
        des HP pour enceinte à évent
      • 2-1-3-4 : Calcul d'une enceinte à évent
      • 2-1-3-5 : Calcul d'une enceinte à triple résonateur
      • 2-1-3-6 : Calcul d'une enceinte à radiateur passif
    • 2-1-4 : Calculs d'une enceinte à radiateur passif
    • 2-1-5 : Calculs d'une enceinte RJ de SUPRAVOX
    • 2-1-6 : Les enceintes closes
      • 2-1-6-1 : Calcul d'une enceinte close
      • 2-1-6-2 : Les enceintes closes
      • 2-1-6-3 : La transformée de Linkwitz
      • 2-1-6-4 : Annuler l'influence de la pièce
        dans les graves
      • 2-1-6-5 : Explication de la recherche multicritères
      • 2-1-6-6 : Recherche multicritères des HP
        pour enceinte close
      • 2-1-6-7 : Comprendre facilement le groupe délai
    • 2-1-7 : Les charges symétriques
      • 2-1-7-1 : Les charges passe-bande du 4e, 6e et 7e ordre
      • 2-1-7-2 : Enceinte passe-bande du 4e ordre
      • 2-1-7-3 : Enceinte passe-bande du 6e ordre
      • 2-1-7-4 : Enceinte passe-bande du 7e ordre
      • 2-1-7-5 : Calcul d'une enceinte passe-bande du 4e ordre
      • 2-1-7-6 : Calcul d'une enceinte passe-bande du 6e ordre
      • 2-1-7-7 : Calcul d'une enceinte passe-bande du 7e ordre
    • 2-1-8 : Les enceintes infinies
      • 2-1-8-1 : Les enceintes infinies
      • 2-1-8-2 : Le PHY-HP KM30
      • 2-1-8-3 : Calcul des enceintes infinies, Vb=9999 L
    • 2-1-9 : Les lignes acoustiques
      • 2-1-9-1 : Les lignes acoustiques
      • 2-1-9-2 : Ligne acoustique pavillonnée
        avec guide d'onde
      • 2-1-9-3 : Réalisation d'enceintes line-array
        MTM, open-baffle et actives
      • 2-1-9-4 : Un projet DIY line-array passif
        haut de gamme
      • 2-1-9-5 : Branchement série/parallèle des haut-parleurs
    • 2-1-10 : Les enceintes TQWT et 1/4 d'onde
      • 2-1-10-1 : Les enceintes TQWT
      • 2-1-10-2 : Les enceintes 1/4 d'onde
      • 2-1-10-3 : Calcul des enceintes 1/4 d'onde et TQWT
      • 2-1-10-4 : Recherche multicritère des haut-parleurs
        pour enceintes 1/4 d'onde
    • 2-1-11 : La hi-fi embarquée, CAR audio
      • 2-1-11-1 : La hi-fi embarquée
      • 2-1-11-2 : Calcul des enceintes hi-fi embarquées
    • 2-1-12 : Les caissons de graves
      • 2-1-12-1 : Le caisson de grave
      • 2-1-12-2 : Les caissons de grave 30 cm
    • 2-1-13 : Stéréolith
      • 2-1-13-1 : L'enceinte JENSEN S100
        et autres Stéréolith
  • 2-2 : Baffles plans
    • 2-2-1 : Théorie du baffle plan
      • 2-2-1-1 : Calcul du court-circuit acoustique
      • 2-2-1-2 : Courbe de réponse du baffle plan
      • 2-2-1-3 : Taille et forme du baffle plan
      • 2-2-1-4 : Choix du haut-parleur
      • 2-2-1-5 : Application du baffle plan
      • 2-2-1-6 : Baffle plan, conclusion et liens
    • 2-2-2 : Grave sur baffle plan
      • 2-2-2-1 : Ajout d'un haut-parleur de grave
      • 2-2-2-2 : Grave de grands diamètres sur baffle plan
      • 2-2-2-3 : Filtrage entre le grave et le large bande
    • 2-2-3 : Réalisation d'un baffle plan
      • 2-2-3-1 : Construction du baffle plan
      • 2-2-3-2 : Baffle plan de médium
      • 2-2-3-3 : Un exemple, le mien
      • 2-2-3-4 : Baffle plan et design
      • 2-2-3-5 : Une enceinte, open baffle, 3 voies
        2x38cm, d'inspiration américaine
      • 2-2-3-6 : Une enceinte, open-baffle 2 x 31 cm,
        inspirée partiellement d'une réalisation DIY
      • 2-2-3-7 : Présentation de deux kits open baffle
      • 2-2-3-8 : Caisson de graves Ripole
    • 2-2-4 : Calcul d'un baffle plan
      • 2-2-4-1 : Explication recherche multicritère
      • 2-2-4-2 : Recherche multicritère
        des haut-parleurs pour baffle plan
      • 2-2-4-3 : Calcul d'un baffle plan
  • 2-3 : Les pavillons
    • 2-3-1 : Pavillons calcul et tracé
      • 2-3-1-1 : Calcul d'un pavillon, couples de
        valeurs longueur et surface
      • 2-3-1-2 : Les pavillons pour les nuls
      • 2-3-1-3 : Formules de calculs des pavillons
      • 2-3-1-4 : Le report des surfaces
      • 2-3-1-5 : Tracé des coudes
      • 2-3-1-6 : Recherche multicritères des HP
        pour pavillon
    • 2-3-2 : Pavillons avant pour compression
      • 2-3-2-1 : Les pavillons avant
      • 2-3-2-2 : Les pavillons pour compression
      • 2-3-2-3 : Pavillons pour compression
        1" RADIAN 475
      • 2-3-2-4 : Les pavillons JMLC
      • 2-3-2-5 : Les pavillons pour smartphone
    • 2-3-3 : Pavillons arrière repliés, BLH
      • 2-3-3-1 : Les pavillons arrière-escargot
      • 2-3-3-2 : Les pavillons arrière BLH ou toboggan
    • 2-3-4 : Plan de pavillons
      • 2-3-4-1 : Caisson de graves à pavillon SONO
      • 2-3-4-2 : Les pavillons courts
      • 2-3-4-3 : Pavillon rond 150 Hz
        Surfaces temporelles
      • 2-3-4-4 : Pavillon rond 150 Hz
        Surfaces JMLC (en attente)
      • 2-3-4-5 : Comparaison pavillon de bas médium
        150 Hz temporel et JMLC
      • 2-3-4-6 : Pavillon carré 150 Hz
        Surfaces temporelles
      • 2-3-4-7 : Pavillon vertical d'encoignure
      • 2-3-4-8 : Klispchorn revisitée
      • 2-3-4-9 : L'enceinte WICKED-ONE HORN FC
  • 2-4 : Les haut-parleurs large bande et coaxiaux
    • 2-4-1 : Les haut-parleurs large bande
      • 2-4-1-1 : Les haut-parleurs large bande
      • 2-4-1-2 : Utilisation des haut-parleurs LB
      • 2-4-1-3 : Médium ou large bande ?
      • 2-4-1-4 : Filtre pour ajouter un tweeter
        à un large bande
      • 2-4-1-5 : La correction de courbe de réponse
        RLC parallèle
      • 2-4-1-6 : Correction de la taille de la face
        avant de l'enceinte
      • 2-4-1-7 : Ma courbe cible
      • 2-4-1-8 : Quantification des critères
    • 2-4-2 : Quelques large bande
      • 2-4-2-1 : Une sélection de haut-parleurs
        large bande de grand diamètre
      • 2-4-2-2 : Le PHY H21LB15
      • 2-4-2-3 : Le PHY KM30
      • 2-4-2-4 : Le VISATON B200
      • 2-4-2-5 : Le DAVIS 20DE8
      • 2-4-2-6 : L'ALTEC 420-8B BILEX
      • 2-4-2-7 : Le JBL LE8T
      • 2-4-2-8 : Haut-parleurs large bande
        sur baffle plan
      • 2-4-2-9 : Une réalisation 31 cm large bande
        en enceinte close
    • 2-4-3 : Les haut-parleurs coaxiaux
      • 2-4-3-1 : Les haut-parleurs coaxiaux
      • 2-4-3-2 : Correction de la taille de la
        face avant de l'enceinte
      • 2-4-3-3 : Ma courbe cible
  • 2-5 : La base de données HP, calculs des enceintes
    • 2-5-1 : Calcul des enceintes
      • 2-5-1-1 : Calcul d'un pavillon
      • 2-5-1-2 : Calcul d'une enceinte bass-reflex
      • 2-5-1-3 : Calcul d'une enceinte à triple
        résonateur
      • 2-5-1-4 : Calcul d'une enceinte à radiateur
        passif
      • 2-5-1-5 : Calcul d'une enceinte passe-bande
        du 4e ordre
      • 2-5-1-6 : Calcul d'une enceinte passe-bande
        du 6e ordre
      • 2-5-1-7 : Calcul d'une enceinte passe-bande
        du 7e ordre
      • 2-5-1-8 : Calcul d'une enceinte 1/4 d'onde
      • 2-5-1-9 : Calcul d'une enceinte close
      • 2-5-1-10 : Calcul d'un baffle plan
      • 2-5-1-11 : Calcul d'un filtre passif,
        2 ou 3 voies, 6 à 24 dB
    • 2-5-2 : Recherches multicritères
      • 2-5-2-1 : Sur les paramètres T&S
      • 2-5-2-2 : Équivalent à celui choisi au départ
      • 2-5-2-3 : HP pour pavillon
      • 2-5-2-4 : HP pour enceinte à évent
      • 2-5-2-5 : HP pour enceinte à évent, BESSEL
      • 2-5-2-6 : HP pour enceinte 1/4 d'onde
      • 2-5-2-7 : HP pour enceinte close
      • 2-5-2-8 : HP pour enceinte CAR AUDIO
      • 2-5-2-9 : HP pour baffle plan
    • 2-5-3 : Consultation des données
      • 2-5-3-1 : T&S par marque et diamètre
      • 2-5-3-2 : T&S d'une liste de HP
      • 2-5-3-3 : Tweeters et compressions
      • 2-5-3-4 : Liste des 50 derniers HP
        entrés ou modifiés
    • 2-5-4 : Ajout et modifications
      • 2-5-4-1 : Ajouter un haut-parleur en base temporaire
      • 2-5-4-2 : Visualiser les haut-parleurs en base temporaire
      • 2-5-4-3 : Modifier vos haut-parleurs en base temporaire
      • 2-5-4-4 : Comparer des haut-parleurs dans les 2 bases
      • 2-5-4-5 : Moyenne des paramètres T&S
    • 2-5-5 : Tableaux
      • 2-5-5-1 : Marques des HP
      • 2-5-5-2 : Avis sur les marques et les HP
      • 2-5-5-3 : Diamètre des HP
      • 2-5-5-4 : Impédance des HP
      • 2-5-5-5 : Type entré et calculé des HP
      • 2-5-5-6 : Type des tweeters et compressions
      • 2-5-5-7 : Type d'enceinte
      • 2-5-5-8 : Type de filtre
      • 2-5-5-9 : Type d'alignement pour enceinte à évent
      • 2-5-5-10 : Combinaisons d'évent par la surface
      • 2-5-5-11 : Proportion des enceintes
      • 2-5-5-12 : Construction des enceintes
    • 2-5-6 : Coeficients, moyennes et courbes
      • 2-5-6-1 : T&S d'un HP équivalent à plusieurs HP
      • 2-5-6-2 : Alignements de THIELE
      • 2-5-6-3 : Moyenne des BL
      • 2-5-6-4 : Moyenne des Xmax
      • 2-5-6-5 : Corrections pour Hi-Fi embarquée
    • 2-5-7 : Fonctionnement
      • 2-5-7-1 : Pourquoi une base de données HP ?
      • 2-5-7-2 : Comment ça marche ?
    • 2-5-8 : Statistiques
      • 2-5-8-1 : Statistiques sur Fs
      • 2-5-8-2 : Statistiques sur Vas
      • 2-5-8-3 : Statistiques sur Qms
      • 2-5-8-4 : Statistiques sur Qes
      • 2-5-8-5 : Statistiques sur Qts
      • 2-5-8-6 : Statistiques sur Fs/Qts
      • 2-5-8-7 : Statistiques sur Vas*Qts²
      • 2-5-8-8 : Statistiques sur Le
  • 2-6 : Le filtrage
    • 2-6-1 : Tweeter et filtre
      • 2-6-1-1 : Choix de la pente du filtre d'un tweeter
      • 2-6-1-2 : Fréquence de résonance du tweeter
      • 2-6-1-3 : Fréquence de coupure des compressions
      • 2-6-1-4 : Le montage MTM, la source concentrique
      • 2-6-1-5 : Le tweeter et l'écoute
      • 2-6-1-6 : Les tweeters piézo-électriques
    • 2-6-2 : Choix du filtre
      • 2-6-2-1 : Filtre 2 et 3 voies et tableur JMLC
      • 2-6-2-2 : Simulateur JMLC filtre 4 voies
      • 2-6-2-3 : Simulateur JMLC filtre 3 voies
      • 2-6-2-4 : Simulateur JMLC filtre 2 voies
      • 2-6-2-5 : Simulation de 4 filtres sous Mathcad
      • 2-6-2-6 : Ordre d'un filtre
      • 2-6-2-7 : Comprendre facilement le groupe délai
      • 2-6-2-8 : Réponse dans l'axe et en coïncidence
      • 2-6-2-9 : L'utopie du filtre à 6 dB/octave
    • 2-6-3 : Calcul des filtres passifs
      • 2-6-3-1 : Les limites du calcul d'un filtre passif
      • 2-6-3-2 : Calcul d'un filtre passif,
        2 ou 3 voies, 6 à 24 dB
      • 2-6-3-3 : Vérification d'un filtre passif existant
        2 voies à 6, 12, 18 et 24 dB/octave
      • 2-6-3-4 : Mise en série de filtres
        du 1er et 2e ordre
      • 2-6-3-5 : La problématique du filtrage d'un grave avec un médium
    • 2-6-4 : Autres filtres passifs
      • 2-6-4-1 : Filtre série et parallèle
        Filtrage avec un HP relais
      • 2-6-4-2 : Filtre passe tout
      • 2-6-4-3 : Filtre pour (ne pas) ajouter
        un tweeter à un LB
      • 2-6-4-4 : Schéma électrique équivalent à un HP
    • 2-6-5 : Filtrer un caisson de graves
    • 2-6-6 : Atténuation et correcteur d'impédance
      • 2-6-6-1 : Égalisation des niveaux
      • 2-6-6-2 : La correction d'impédance
        RC série
      • 2-6-6-3 : La correction d'impédance
        RLC série
      • 2-6-6-4 : La correction d'impédance
        RC et RLC série
      • 2-6-6-5 : La correction de courbe de réponse
        RLC parallèle
    • 2-6-7 : Réalisation des filtres passifs
      • 2-6-7-1 : Les filtres passifs du commerce
      • 2-6-7-2 : Réalisation sur une plaquette en bois
      • 2-6-7-3 : Mise au point d'un filtre passif
      • 2-6-7-4 : Choix des selfs
      • 2-6-7-5 : Résistance interne des selfs
      • 2-6-7-6 : La longue mise au point d'un filtre
      • 2-6-7-7 : Tweak DIY des filtres passifs des enceintes du commerce
    • 2-6-8 : Filtre actif
      • 2-6-8-1 : Les filtres actifs
      • 2-6-8-2 : Filtres actifs BEHRINGER DCX 2496
      • 2-6-8-3 : Filtrage dans un PC
      • 2-6-8-4 : Le filtre actif passif KANEDA
    • 2-6-9 : Autour des filtres
      • 2-6-9-1 : La mise en phase des HP
      • 2-6-9-2 : Phase et temps de propagation
        de groupe d'un filtre
      • 2-6-9-3 : Branchement série/parallèle de
        plusieurs HP et impédance
      • 2-6-9-4 : Remplacement d'un tweeter
  • 2-7 : Réalisations et plans
    • 2-7-1 : Plans avec les outils de la base de données
      • 2-7-1-1 : Lire un plan d'enceinte,
        sélection multicritères
      • 2-7-1-2 : Lire un plan d'enceinte,
        sélection par le numéro
      • 2-7-1-3 : Créer un plan d'enceinte
    • 2-7-2 : Plans de la menuiserie de votre enceinte
      • 2-7-2-1 : Remarques
      • 2-7-2-2 : Volume occupé par l'évent et le HP
      • 2-7-2-3 : Personalisation de la réalisation
      • 2-7-2-4 : Tracé de la face avant
      • 2-7-2-5 : Réalisation pratique d'une enceinte
      • 2-7-2-6 : Finition par placage d'une enceinte
      • 2-7-2-7 : Finition à la peinture d'une enceinte
    • 2-7-3 : Critères importants à prendre en compte
      • 2-7-3-1 : Proportions des enceintes
      • 2-7-3-2 : Position en hauteur du HP de graves
      • 2-7-3-3 : Où placer les tasseaux de renfort ?
      • 2-7-3-4 : Pieds pour enceinte
      • 2-7-3-5 : Ajouter des roues à une enceinte
      • 2-7-3-6 : L'amortissement interne
      • 2-7-3-7 : La soudure
    • 2-7-4 : La mise au point, filtre et enceinte
      • 2-7-4-1 : Vos oreilles, parce qu'il faut bien
        entendre pour faire une bonne mise au point
      • 2-7-4-2 : Mesures et mise au point :
        Contexte et méthode
      • 2-7-4-3 : La mise au point et le rodage
      • 2-7-4-4 : La mise au point du filtre
      • 2-7-4-5 : La longue mise au point d'un filtre
      • 2-7-4-6 : La mise au point de l'évent
      • 2-7-4-7 : Un exemple de mise au point
      • 2-7-4-8 : Mettez au point vous-même vos
        enceintes haut de gamme, par Gautier Audio
    • 2-7-5 : Réalisations 8, 10, 12 et 14 cm
      • 2-7-5-1 : Réalisation HM130G14 + TW025A0
      • 2-7-5-2 : Le FOSTEX FE127E en simple BR
    • 2-7-6 : Réalisations 17 cm
      • 2-7-6-1 : Une enceinte utilisable en passif
        et en actif inspirée d'une colonne anglaise
      • 2-7-6-2 : Une enceinte semi-DIY haut de gamme
        2x17cm inspirée du moniteur Kinoshita KM1V
      • 2-7-6-3 : Enceinte MTM Giulia et
        chaîne audio associée
      • 2-7-6-4 : Simulation du HP FOSTEX FE167E
      • 2-7-6-5 : FOSTEX FE168E SIGMA
    • 2-7-7 : Réalisations 21 cm
      • 2-7-7-1 : Un projet d'enceinte passive DIY
        4x20cm à base de composants Klipsch
      • 2-7-7-2 : BR à résonateur HP FOSTEX FE207E
    • 2-7-8 : Réalisations 25 cm
      • 2-7-8-1 : Un projet DIY, 3 voies actives
        25 cm, inspirée d'une enceinte chinoise
      • 2-7-8-2 : Une enceinte active ou passive,
        3 voies, 25 cm, d'allure combo vintage
      • 2-7-8-3 : Une enceinte inspirée partiellement
        d'un moniteur de studio JBL de 25cm
      • 2-7-8-4 : Une enceinte semi-DIY, 2 x 25cm,
        inspirée d'une enceinte mixte studio hi-fi
      • 2-7-8-5 : L'installation de Jean-Pierre
    • 2-7-9 : Réalisations 31 cm
      • 2-7-9-1 : Un projet d'enceinte sur la base d'une
        compression 1,4 pouce et d'un grave médium
        de 31 cm
      • 2-7-9-2 : Une enceinte hi-fi active 3 voies DIY,
        inspirée par une enceinte connue
      • 2-7-9-3 : Une enceinte 3 voies, 2x31 cm,
        active, inspirée par une enceinte allemande
      • 2-7-9-4 : Une 3 voies avec 2x31 cm, active,
        sans menuiserie, haut-parleurs Davis Acoustics
      • 2-7-9-5 : Câbler et dupliquer
        un moniteur de studio pour un projet DIY
      • 2-7-9-6 : Une enceinte active, 3 voies,
        inspirée par une Cabasse Sampan
      • 2-7-9-7 : Une enceinte hi-fi inspirée d'un
        moniteur d'écoute principale Adam Audio S6X
      • 2-7-9-8 : Une enceinte DIY haut de gamme
        inspirée d'une enceinte hi-fi anglaise
      • 2-7-9-9 : Une enceinte, 2x31 cm, à deux
        pavillons, inspirée d'une enceinte chinoise
      • 2-7-9-10 : Graves de 31 cm pour enceinte close
    • 2-7-10 : Réalisations 38 cm
      • 2-7-10-1 : Projet d'enceinte amplifiée,
        3 voies/38 cm, basée sur des HP JBL
      • 2-7-10-2 : Une enceinte DIY, 2x38 cm,
        inspirée d'une enceinte hi-fi américaine
      • 2-7-10-3 : Une enceinte semi-DIY, 2x38 cm,
        inspirée d'une enceinte anglaise
    • 2-7-11 : Réalisations 46 cm
      • 2-7-11-1 : Un trois 46cm DIY inspiré par
        un subwoofer thaïlandais et un kit américain
      • 2-7-11-2 : Un projet inspiré d'une
        enceinte associant Line-source et point-source
      • 2-7-11-3 : Une enceinte DIY, 46cm, inspirée
        partiellement d'un kit danois
      • 2-7-11-4 : Des éléments JBL pour une enceinte
        46cm d'inspiration JBL 4699B
  • 2-8 : Quelques aspects du cahier des charges,
    par Jean Dupont
    • 2-8-1 : Philosophie sur la Hi-Fi,
      par Jean Dupont
      • 2-8-1-1 : Le clivage entre Hi-Fi et moniteur de studio
        en Grande-Bretagne et en Allemagne
      • 2-8-1-2 : La voie grave de Marcel Roggero
        30 ans plus tard
      • 2-8-1-3 : La voie grave de Francis Ibre
        15 ans plus tard
      • 2-8-1-4 : Un hommage à Jean-Michel
        LE CLéAC'H (1954-2013)
      • 2-8-1-5 : Une alimentation par des batteries
        pour une meilleure qualité sonore
      • 2-8-1-6 : Le vocabulaire et les expressions
        audiophiles
      • 2-8-1-7 : Réfuter un pseudo-manifeste
        audiophile
      • 2-8-1-8 : Une quantification hi-fi au moyen
        d'un questionnaire
    • 2-8-2 : Philosophie de conception,
      par Jean Dupont
      • 2-8-2-1 : Une solution haut rendement sous
        contrainte de budget et d'encombrement
      • 2-8-2-2 : Concilier, look vintage, qualité d'écoute,
        budget serré et relative facilitée ?
      • 2-8-2-3 : Faire appel à un artisan
        menuisier-ébéniste pour une enceinte
      • 2-8-2-4 : L'association d'enceintes de studio
        comme alternative à certaines réalisations DIY THDG
      • 2-8-2-5 : Utilisation d'un autotransformateur
        en amplification active 3 voies
      • 2-8-2-6 : Erreurs et faiblesses de certaines
        enceintes japonaises, dites "audiophiles"
        et " haut rendement"
      • 2-8-2-7 : Mieux déceler les erreurs des
        systèmes japonisants
      • 2-8-2-8 : Des erreurs rencontrées dans
        des projets et réalisations d'enceintes DIY
    • 2-8-3 : Haut-parleurs pour le grave,
      par Jean Dupont
      • 2-8-3-1 : Dans quelle mesure une enceinte
        comportant un double 38 cm est-elle dépassée ?
      • 2-8-3-2 : Un double 31 cm comme alternative
        à un 46 cm ?
      • 2-8-3-3 : Le subwoofer array en Hi-Fi
      • 2-8-3-4 : Comparaison de deux haut-parleurs
        de 38 cm à faible masse mobile
  • 2-9 : La sonorisation
    • 2-9-1 : Enceinte de sono à 2 voies
    • 2-9-2 : Fabrication enceinte de sono à 2 voies
    • 2-9-3 : Fréquence de coupure compressions
    • 2-9-4 : Caisson de graves pour sono
    • 2-9-5 : Le SPL max des caissons de basse
      actifs de sonorisation mobile
    • 2-9-6 : Caisson de graves à pavillon pour sono
    • 2-9-7 : Enceinte de bas médium pour sono
    • 2-9-8 : Puissance des enceintes BM sono
    • 2-9-9 : Puissance des enceintes graves sono
    • 2-9-10 : Ajouter des roues à une enceinte
  • 2-10 : Le home cinéma et ses réglages
    • 2-10-1 : Home cinéma et haute fidélité
    • 2-10-2 : Home cinéma : La famille sonore
    • 2-10-3 : Home cinéma : Sélecteurs
    • 2-10-4 : Les réglages en home cinéma
    • 2-10-5 : Home cinéma : L'enceinte centrale
    • 2-10-6 : Home cinéma et Hi-Fi : Une autre vision
    • 2-10-7 : Une enceinte professionnelle de cinéma
    • 2-10-8 : La réponse en peigne des enceintes centrales
• 3 : Mon système, autres sujets
  • 3-1 : Du 4 voies au large bande
    • 3-1-1 : La configuration à 4 voies
    • 3-1-2 : Le passage à 3 voies
    • 3-1-3 : Le passage à 2 voies
    • 3-1-4 : Un premier large bande
  • 3-2 : Ajouter un grave au large bande
    • 3-2-1 : Grave sur baffle plan
    • 3-2-2 : Mes baffles plans filtrés en passif
  • 3-3 : Bi et tri amplification active
    • 3-3-1 : Biamplification active
    • 3-3-2 : Triamplification active
    • 3-3-3 : Triamplification avec le LB SIARE alnico
    • 3-3-4 : Le DCX 2496
  • 3-4 : D'autres haut-parleurs large bande
    • 3-4-1 : Avec le MONACOR SP-200X
    • 3-4-2 : Avec le VISATON B200
    • 3-4-3 : Ajouter un égaliseur
    • 3-4-4 : MTM et U-FRAME
    • 3-4-5 : Travailler le filtrage
    • 3-4-6 : Corriger la phase acoustique
  • 3-5 : Retour progressif au large bande seul
    • 3-5-1 : La transformée de Linkwitz
    • 3-5-2 : Le DAVIS 20DE8
    • 3-5-3 : L'ALTEC 420-8B BILEX
    • 3-5-4 : Bilan de ces expériences
  • 3-6 : Annexes
    • 3-6-1 : Le tweak du lecteur CD PHILIPS CD723
    • 3-6-2 : Panne sur le HAFLER TA 1600
    • 3-6-3 : Le VISATON B200 en images
  • 3-7 : Changement d'énergie de chauffage
    • 3-7-1 : Le chauffage central électrique
    • 3-7-2 : La solution initiale
    • 3-7-3 : Les solutions de rechange
    • 3-7-4 : Dimensionnement de la solution
    • 3-7-5 : Abonnement électrique jour / nuit
    • 3-7-6 : Devis et bilan financier
      mis à jour en novembre 2021
    • 3-7-7 : Installation pratique
    • 3-7-8 : Dimensionnement de votre installation
    • 3-7-9 : Vos avis
    • 3-7-10 : Pompe à chaleur
    • 3-7-11 : Panneaux solaires
  • 3-8 : 205 km sur le chemin de Compostelle
  • 3-9 : Les émissions musicales à la télé
  • 3-10 : Le coin du râleur
  • 3-11 : Éclairage en haut d'une armoire
• 4 : Le site, contact, liens, recherches
  • 4-1 : Accueil
  • 4-2 : Première page du site
  • 4-3 : Contact, écrivez-moi
  • 4-4 : Lexique
  •  
  • 4-5 : Mentions légales
  • 4-6 : Déontologie et participation
  • 4-7 : Validation W3C des pages
  • 4-8 : Compteur
  •  
  • 4-9 : Moteur de recherche dans le site
  • 4-10 : Liens, les différents chapitres de ce site
  • 4-11 : Liens, marques de HP et paramètres T&S
  • 4-12 : Les PDF et compléments de Jean Dupont
  • 4-13 : Liens extérieurs au site
  •  
  • 4-14 : Images et Web

 

2-3-2-3 : Pavillon pour compression 1" RADIAN 475

Mise à jour : 15 septembre 2023, Antimode 11.

 

Pourquoi ce chapitre ?

Dans le chapitre sur le report des surfaces entre le calcul dans la feuille sous EXCEL et le tracé sur le plan, j'ai expliqué comment faire le report avec différents types de surfaces, planes, sphériques, cylindriques, JMLC, temporels.
Cette analyse montre, avec la méthode de contrôle retenue, que les surfaces temporelles sont meilleures que les autres, y compris les surfaces JMLC.

J'ai parlé de cette analyse sur plusieurs forums, dont certains spécialisés dans les pavillons, sans avoir les retours attendus.
Je peux comprendre une certaine peur d'aller vers l'inconnu, je ne comprendrai jamais une analyse erronée.
Même en expliquant en long, large et travers que la croissance des sections d'un pavillon JMLC ne se fait pas au bon endroit, nombreux ceux qui refusent de voir la réalité en face.

Face à l'obscurantisme, et voulant tout de même promouvoir ce type de surfaces, j'ai décidé de faire un plan libre de droits qui respecte scrupuleusement un certain nombre de règles de conception auquel je tiens.
Ce plan est réalisé pour un internaute qui le réalisera sur une machine à commande numérique, et qui fournira les illustrations et avis d'écoute utilisés dans ce chapitre.

 

Libre de droits :

N'importe qui peut reprendre ce plan, le réaliser, le vendre sous sa marque, sans que je puisse trouver quoi que ce soit à redire.
Ce point est surtout vrai pour le pavillon circulaire ou toutes les côtes sont données.
Pour le pavillon rectangulaire, il faudra me demander les 3D pour la réalisation sur machines à commandes numériques.
Je suis un amateur indépendant de toutes contraintes commerciales, j'ai un travail pour vivre, je ne ferai pas d'argent avec ce plan.
Par contre si vous voulez une évolution en 2", une adaptation à une autre compression ou haut-parleurs, ce sera un plan privé que vous devrez acheter.
Nous n'en sommes pas encore là.

Nous ne sommes pas dans le monde des bisounours, et je ne me fais aucune illusion, mais je crois en l'honnêteté du plus grand monde.
J'aimerai, mais je ne peux pas l'exiger parce que le plan est libre de droits, que le terme "Surfaces temporelles" soit indiqué.
Google est notre ami, le site est bien référencé (à l'outrance disent ceux qui n'ont rien compris), les liens reviendront automatiquement sur mes pages, et la paternité me reviendra de fait sans que vous ayez à l'indiquer explicitement.

 

Cône de sortie de la compression et loi d'expansion :

 

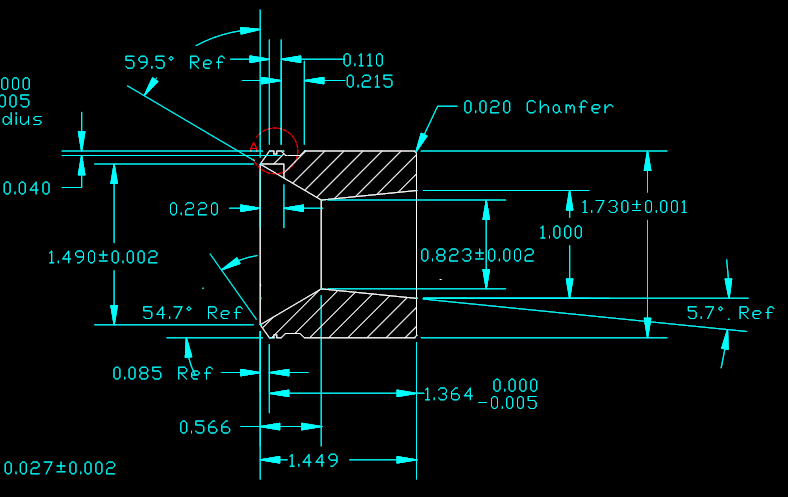
Le cône de sortie est parfaitement défini sur le plan : Diamètre 0.823 et 1.000 pouces, longueur 1.449 - 0.566 pouces. 1 pouce = 25.4 mm.
Le pavillon doit se raccorder exactement à la compression, en surface et avec le respect des tangentes.
Par conséquent nous ne pouvons pas choisir la loi d'expansion, nous prendrons celle qui permet le raccordement exact à la compression avec les règles ci-dessus.
C'est la stricte application d'un article de l'audiophile sur "Le dressage des escargots", article dont je ne retrouve pas le lien sur internet, mais que j'avais en version papier dans ma collection complète des revues l'Audiophile.

Le cône de sortie de cette compression RADIAN 475 ouvre à 11.446°.
Le centre du cône se trouve à 126.713 mm du plan d'appui de la compression sur le pavillon.
Étant donné que la surface est sphérique à ce niveau, le "0" des longueurs du pavillon est décalé de 0.635 mm par rapport au plan d'appui de la compression sur le pavillon.
La surface sphérique est de 507.974 mm², alors que la surface plane pour un diamètre de 25.4 mm est de 506.707 mm².
Je ne chipote pas avec la précision, les arrondis ne doivent se faire qu'a la réalisation...

 

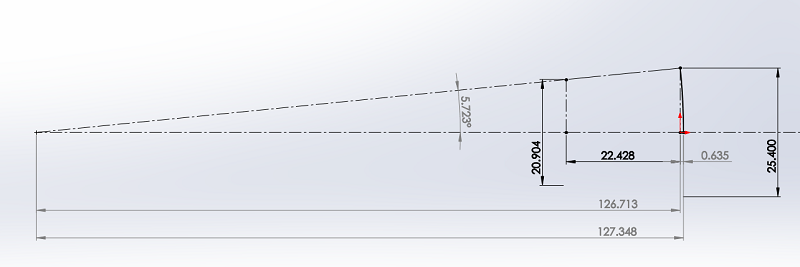
Une première vérification, avec des surfaces planes, et une loi d'expansion exponentielle :

La loi est S = So EXP( M * L ) ou encore M = 1 / L * LN( S / So) avec L = 0.02248 m, So = 20.904² * Pi / 4 = 343.20 mm2, S = 25.4² * Pi / 4 = 506.71 mm2.
M = 1 / 0.02248 * LN( 506.71 / 343.20 ) = 17.37 m^-1.
F = C * M / 4 / Pi = 344 * 17.37 / 4 / Pi = 475.6 Hz.
Cette compression permet de faire :

• Un pavillon exponentiel capable de reprendre au minimum à 475.6 * 2.5 = 1200 Hz.
• Un pavillon hyperbolique capable de reprendre au minimum à 475.6 * 1.5 = 715 Hz.

 

Un calcul plus précis avec des surfaces sphériques et une loi d'expansion hyperbolique :

2 mm après la première section du début de la compression j'ai tracé une 2^e surface toujours dans le prolongement du cône de sortie.
Cette section sphérique fait 524.054 mm².
EXCEL va nous permettre de trouver quelle loi d'expansion hyperbolique T=0.707 passe par une section initiale de 507.974 mm², et par une 2^e section à 2 mm de distance de 524.054 mm².
Inutile de passer par de longues équations pour cela, la fonction EXCEL "valeur cible" trouve la solution très rapidement.

 

 

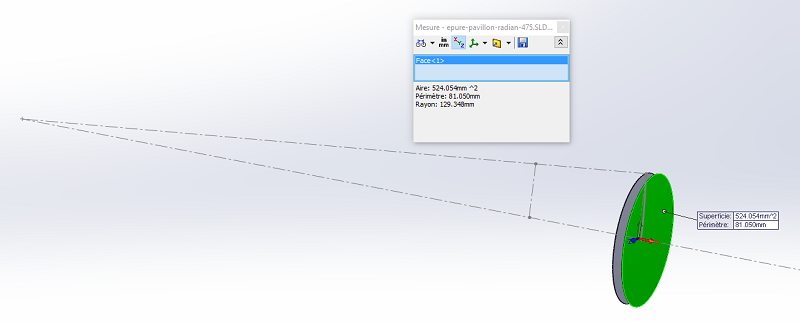
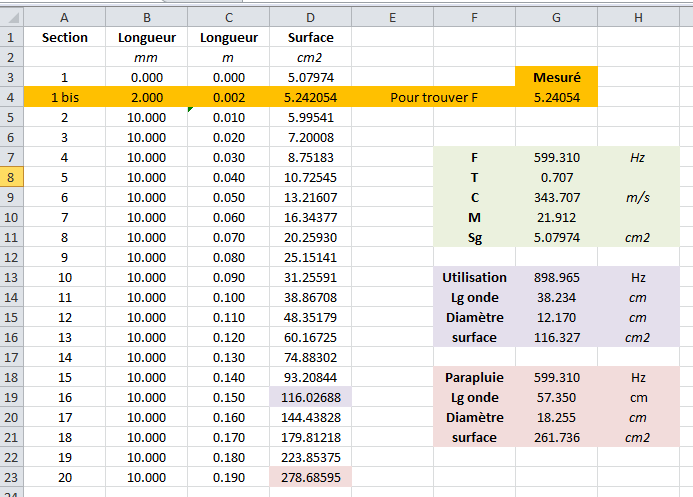
Cette compression permet une loi d'expansion hyperbolique avec T=0.707 calculée pour 600 Hz, avec un raccordement irréprochable à la compression.

• L'utilisation est possible au-dessus de 1.5 * 600 = 900 Hz.
  Le diamètre à la bouche du pavillon sera de 12.2 cm et la longueur du pavillon de 15 cm.
  C'est une réalisation sans compromis au juste nécessaire.
   
• Il est possible de faire un pavillon qui descend en surface à 600 Hz, avec un diamètre de bouche de 18.3 cm et une longueur du pavillon de 19 cm.
  C'est une réalisation "papapluie" qui permet sans doute un raccordement plus facile avec un haut-parleur de trop grand diamètre.

 

Tracé du pavillon :

Lorsque l'on jette un caillou dans l'eau, les ondes qui se forment à la surface sont circulaires.
C'est donc la base du tracé du pavillon, respecter la circularité des ondes.
Sur cette base je ferai une 2^e version rectangulaire en agrandissant dans un plan et en rétrécissant dans l'autre.
Pour reprendre mon analogie avec l'eau, ce sont des digues que je déplacerai à ma convenance, pour canaliser les ondes comme souhaité.

 

Tracé du pavillon circulaire à surfaces temporelles :

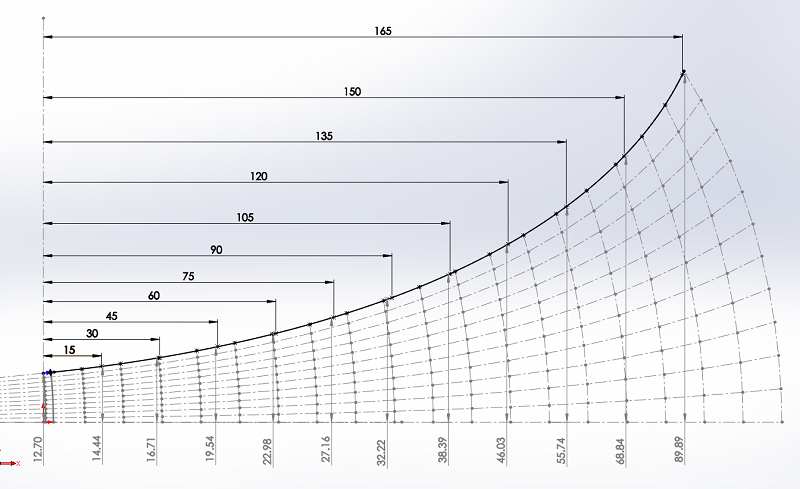
Esquisse du pavillon, pour avoir la surface de chaque section.
Les valeurs de rayons et longueurs sont reportées dans un tableau sous EXCEL un peu plus bas dans le chapitre.

 

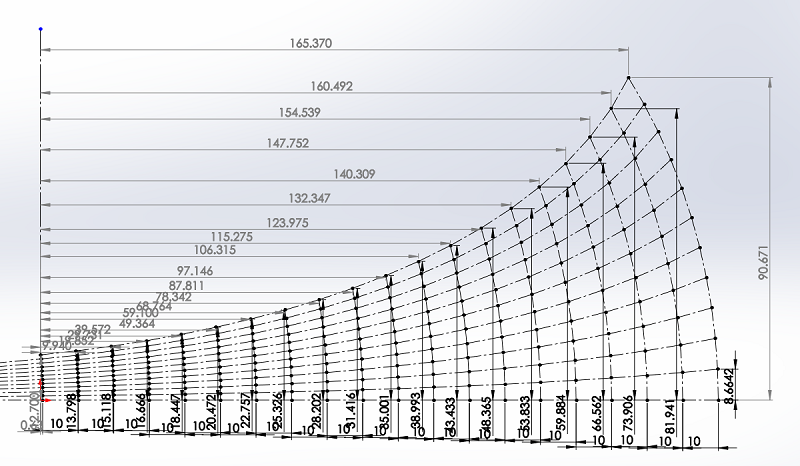
Vérification de la 15^e section, il fallait en choisir une pour l'exemple !!!
La valeur mesurée sur le plan est de 9320.7 mm², la valeur calculée par EXCEL est de 9320.8 mm².
Pour être plus précis que les 0.1 mm², il faut côter le plan au 1/10^e de micron.
Ce sera sans moi parce que si vous arrivez à une réalisation au 1/10^e de mm sur un pavillon en bois, ce sera déjà une très belle performance.

 

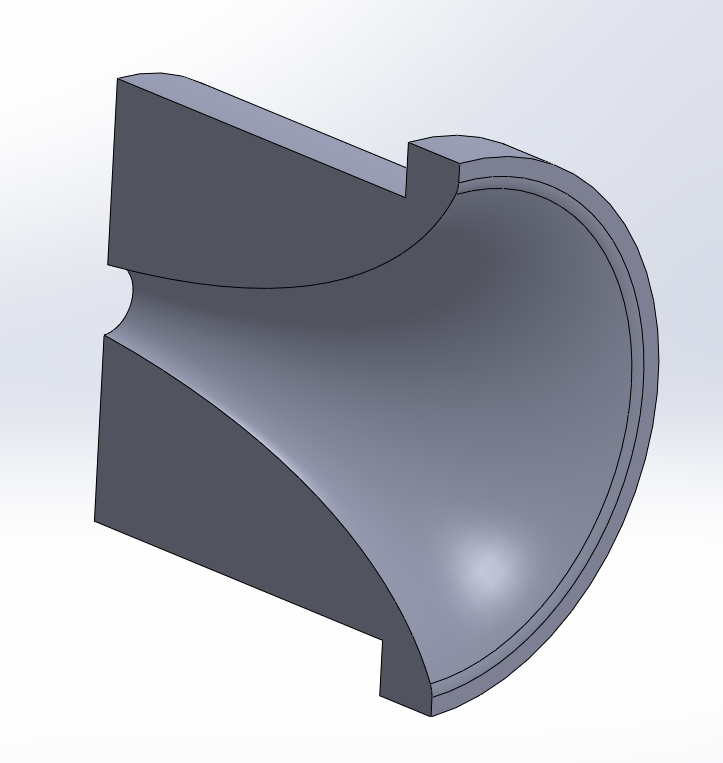
Les côtes de réalisation, colonnes G et H.
Vous devez au minimum aller jusqu'à la section 16 pour avoir un pavillon utilisable au-dessus de 900 Hz.
Si vous allez jusqu'à la section 20, loi d'expansion et surface de bouche permettent le 600 Hz théorique, et le 900 Hz pratique sans aucun compromis.

 

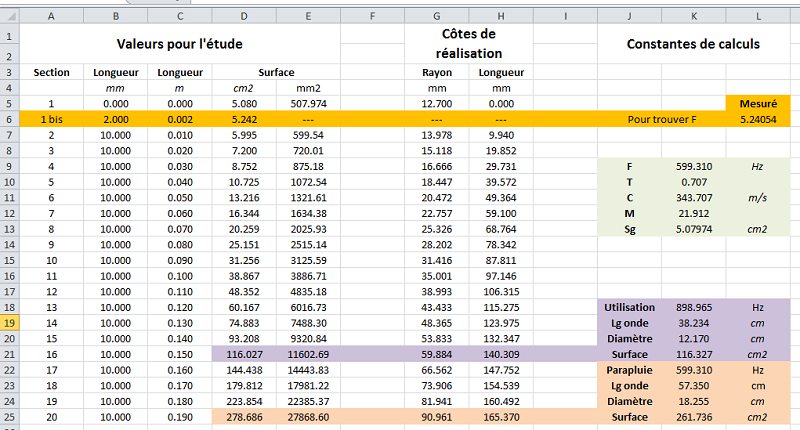
Une vue 3D en coupe du pavillon.

 

Pour la réalisation, il faut faire un empilement de rondelles de bois vissées entre elles.
Idéalement l'usinage doit se faire sur un tour à bois à commande numérique.
Une découpe de chaque rondelle, extérieure et intérieure, à la scie sauteuse ou à la défonceuse est également possible, suivit d'un ponçage final.
La première rondelle, celle contre laquelle est vissée la compression, doit rester démontable.
Ci-dessous les côtes de réalisation pour des planches en médite ou CTP de 10 et 15 mm d'épaisseur.
Sur demande je peux ajouter d'autres épaisseurs.

 

 

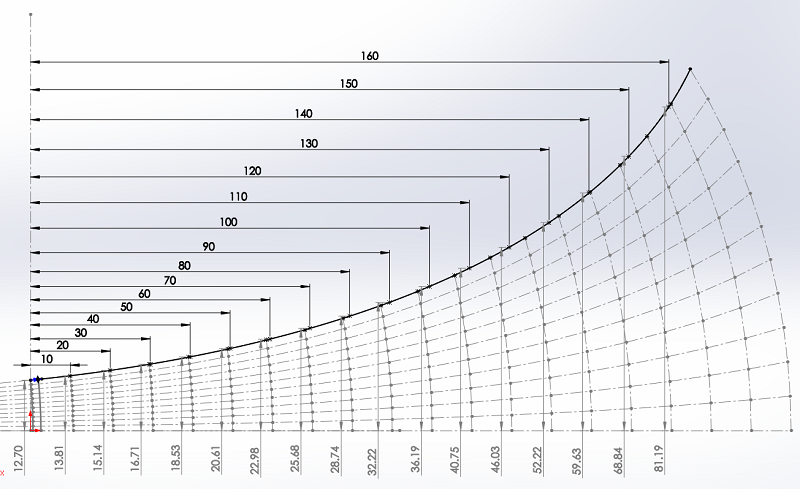
Tracé du pavillon pseudorectangulaire à partir du pavillon circulaire :

Ce n'est pas par hasard que j'ai commencé par tracer le pavillon circulaire, c'est la base de départ pour tracer le pavillon pseudorectangulaire.
Les lignes de construction, les surfaces, seront agrandies, et retaillées pour passer progressivement d'une section ronde à une section pseudorectangulaire avec un raccord parfait avec la compression.
En pratique les sections seront des ellipses, les seules qui permettent de passer de façon continue d'une section ronde à une section plus large que haute.
Les ellipses seront "enroulées" sur les surfaces temporelles (enroulé est le terme CAO).
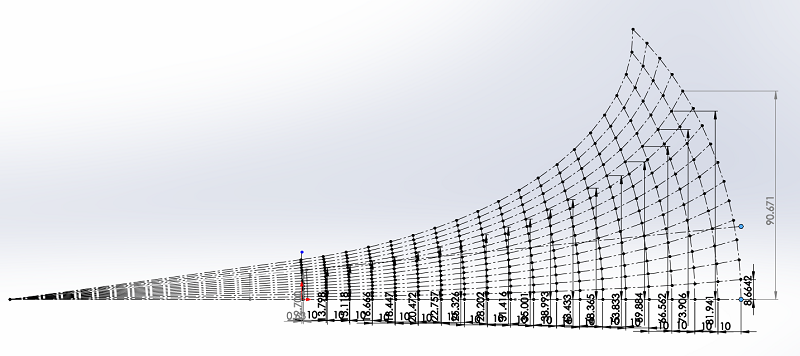
Le résultat sera un modèle 3D pour CAO, modèle qui ne pourra pas être côté, ou qui serait trop compliqué à côter.

Sur l'esquisse ci-dessous, j'ai agrandi les sections en ajoutant des 4 éléments de construction par section.
Une remarque en passant, essayez de faire la même chose avec une construction JMLC des surfaces !!!
J'ai aussi prolongé la droite qui prolonge le cône de la compression, les premières sections du pavillon rectangulaire grandiront dans la direction verticale en suivant cette droite, jusqu'à avoir une ouverture horizontale de 90° environ.
Une fois les 90° horizontaux atteint, l'ouverture sera conservée et la croissance se fera suivant la direction verticale.

 

Et en 2023 ?

Si je devais vérifier le pavillon avec Hornresp, il ne serait pas bon.
Pour qu'il soit bon, il faudrait :

• Une loi d'expansion exponentielle.
• Des surfaces planes.
• Un diamètre extérieur qui permet de passer le 475 Hz, avec une fréquence basse limite de 475 Hz.

Un autre logiciel de calcul des pavillons pourra donner d'autres conclusions, mais je n'ai pas cet autre logiciel plus performant...

 

Dôme Acoustique