| Page affichée à 13:32:58 samedi 21 décembre 2024 Ce site n'utilise pas de cookie |
 |
Dôme acoustique | Compteur pour tout le site : 17 185 357 Nombre actuel de lecteurs : 390 Les menus pour smartphone. |
Faire un don par PayPal |
| Le site de Dominique, un amateur passionné |
2-1-6-2 : Enceinte acoustique close
Mise à jour : 6 juillet 2023, Antidote 11.
Baffle plan :
Les haut-parleurs électrodynamiques rayonnent par les deux faces de leur membrane, on appelle cela un fonctionnement en dipôle.
Lors du mouvement de la membrane vers l'avant, il y a la création d'une onde de pression sur la face avant du haut-parleur.
L'onde créée par la face arrière est alors une onde de dépression.
Si on ne fait rien, ces deux ondes vont s'annuler, et il n'y aura pas création de son.
Une expérience très simple, pour vérifier cet aspect physique, consiste à alimenter un haut-parleur de graves (donc capable de reproduire des fréquences graves) posé nu sur une table, avec un signal sinusoïdal de 50 Hz : Si l'on perçoit bien les mouvements de la membrane, le son émis est très faible.Ce court-circuit acoustique dû au fonctionnement en dipôle impose au minimum la mise en place d'un écran qui sépare les ondes avant et arrière.
Le court-circuit acoustique cesse lorsque les dimensions de l'écran qui sépare les ondes avants et arrières sont suffisamment grandes devant la longueur d'onde du son le plus grave que l'on souhaite reproduire.Le temps mis par les vibrations de l'air, qui se propagent à une vitesse C (343.707 m/s à 20°C, 40% d'humidité relative et 50 m d'altitude) pour contourner un écran plan et circulaire de diamètre D, est t = D/c.
Les pressions s'équilibrent et se neutralisent (il n'y a plus de son émis) lorsque ce temps t coïncide avec la période T ( inverse de la fréquence f) du signal sonore T = 1/f = D/c.Connaissant la fréquence la plus basse à reproduire, une bonne séparation entre les ondes avant et arrière ne peut être obtenue que dès lors que D > c/f.
Ceci impose les dimensions minimales de l'écran en fonction de la fréquence la plus basse que l'on souhaite reproduire.Le tableau ci-après donne la valeur de la longueur d'onde pour quelques fréquences de 20 à 10 000 Hz, la vitesse du son dans l'air est prise égale à 340 m/s, les longueurs d'onde sont indiquées en mètres.
| Fréquence | Long. Onde | Fréquence | Long. Onde |
|---|---|---|---|
| 20 | 17,00 | 1 000 | 0,34 |
| 50 | 6,80 | 2 000 | 0,17 |
| 100 | 3,40 | 5 000 | 0,068 |
| 200 | 1,70 | 10 000 | 0,034 |
| 500 | 0,68 | 20 000 | 0,017 |
On voit d'après ce tableau que pour un rayonnement effectif jusqu'à la fréquence la plus basse théorique de 20 Hz, il faudrait théoriquement un écran d'au moins 17 m de diamètre.
On voit aussi que pour une fréquence de 1000Hz, il suffit de monter le haut-parleur de médium dans un écran de 34 cm de diamètre pour éviter le court-circuit acoustique.
Pour reproduire 5 000 Hz on n'a plus besoin que d'un écran de 6,8 cm ce qui ressemble aux dimensions hors tout d'un haut-parleur d'aigus qu'on montera sans baffle pour échapper aux phénomènes de diffractions.
On conçoit alors l'inconvénient théorique d'un écran pour l'usage domestique des haut-parleurs de grave d'où l'intérêt par exemple de neutraliser complètement les effets de l'onde arrière en mettant le haut-parleur dans un coffret clos.Le paragraphe suivant présente les principes de la réalisation et de la modélisation des enceintes closes.
Réalisation des enceintes closes :
Un haut-parleur électrodynamique se caractérise par 5 caractéristiques physiques fondamentales (2 électriques et 3 mécaniques) que l'on mesure facilement.
Les deux caractéristiques électriques sont :
- La résistance Re de sa bobine mobile.
- L'inductance Le de sa bobine mobile.
Les trois caractéristiques mécaniques sont :
- La masse Mms de son équipage mobile.
- La compliance Cms de la suspension de la membrane (spider et suspension périphérique), qui représente l'effet ressort ( la compliance est l'inverse de la raideur elle s'exprime en m/N) de cette suspension.
- Les pertes mécaniques que l'on appelle Rms (pertes par frottement interne des suspensions, pertes par le rayonnement acoustique de la membrane (et oui c'est assimilable à une perte, puisque le rayonnement acoustique est bien quelque chose que perd le haut-parleur au profit de son environnement extérieur, en l'occurrence l'air ambiant sous la forme d'une émission sonore), etc.)
D'un point de vue physique, un coffret clos par le comportement de l'air qu'il contient lors des mouvements d'avant en arrière de la membrane, va se comporter comme un ressort supplémentaire (de raideur K) qui s'ajoute au ressort de la suspension du haut-parleur.
L'effet ressort de l'air dans le coffret n'est pas dans l'absolu une fonction linéaire du déplacement de la membrane.
Mais pour les petits signaux et dans une plage de fonctionnement ou x * Sd << Vb, c'est à dire quand x le déplacement de la membrane multiplié par la surface projetée Sd du haut-parleur ne dépasse pas 2 à 5% de VB, on trouve par un développement approché de l'expression théorique que K = g * Sd / Vb.
K peut donc être considéré comme constant dans l'hypothèse de mouvements de la membrane pas trop importants.
On conçoit bien que l'air contenu dans un petit coffret de volume Vb1, aura dans la pratique un comportement plus raide (K1 > K2), que l'air contenu dans un grand coffret de volume Vb2.
L'air contenu dans le coffret va ainsi agir sur les mouvements de la membrane en s'y opposant d'autant plus que le volume Vb est petit et réciproquement.Dans la pratique la réalisation d'une enceinte close est quelque chose de relativement simple que l'on peut décomposer en deux étapes :
- La première étape a pour but de mettre le haut-parleur dans un coffret rigoureusement clos (étanchéité) et contenant du matériel absorbant pour annuler où amortir le mieux possible l'onde arrière du haut-parleur, donc éviter par cette ablation le court-circuit acoustique latent et minimiser les effets pervers de cette onde acoustique arrière (résonance de coffret, etc.)
- La deuxième étape consiste à faire le choix d'un volume judicieux Vb.
C'est-à-dire choisir la bonne raideur K qu'apportera l'air contenu dans le coffret et qui viendra (comme déjà vu) s'ajouter à la raideur (1/Cms) existante de la suspension de la membrane pour atteindre le fonctionnement visé par le concepteur (cahier des charges).Pour un haut-parleur donné, il n'y a donc ainsi qu'un seul paramètre de liberté lorsque l'on souhaite optimiser une enceinte close, c'est la valeur optimale de K et donc du volume Vb qui en découle.
Dans la pratique l'étude d'une enceinte acoustique close est ramenée à l'étude d'un filtre électrique passe-haut.
On préfère concrétiser alors par convention (théorie des filtres) ce seul paramètre de liberté nécessaire à l'optimisation d'une enceinte close et son HP, par le coefficient de surtension total Qtc.
C'est d'ailleurs un paramètre très astucieux pour décrire simplement la réponse du haut-parleur aux basses fréquences.Optimiser une enceinte close revient ainsi à rechercher le Qtc qui répond le mieux au cahier des charges, c'est-à-dire à l'objectif recherché (meilleur rendement, puissance maximale admissible, forme de la réponse dans les graves, etc.)
Modélisation des enceintes closes
Le comportement acoustique d'un haut-parleur monté dans un coffret clos sera très voisin en termes de modélisation (avec l'effet de court-circuit acoustique en moins) du comportement qu'aurait le même haut-parleur nu.
Seule la raideur qui s'oppose aux mouvements de l'équipage mobile est différente.
On peut donc prédire que la fréquence de résonance du haut-parleur monté dans un coffret clos sera plus haute que celle du même haut-parleur nu.Avant d'aborder la modélisation d'une enceinte close, le paragraphe suivant propose un simple rappel sur les principes généraux que l'on utilise depuis les travaux de THIELE et SMALL, pour modéliser les haut-parleurs et leurs montages dans des enceintes acoustiques.
Le haut-parleur est un transducteur
Le haut-parleur est un transducteur, car il traduit des signaux électriques, en un mouvement mécanique (ceux de la membrane) puis en signaux acoustiques (c'est ce qu'on entend).
Pour ce faire, celui-ci est constitué d'un moteur électrique ( aimant + bobine mobile) qui est couplé (la bobine mobile est collée physiquement à la membrane) à un système mécanique (la membrane + suspension).
Le système mécanique est couplé au système acoustique, c'est-à-dire à l'air ambiant, c'est le rayonnement de la membrane considéré comme un piston infiniment rigide.
Lord Rayley a jeté les bases et résolu l'équation différentielle du rayonnement acoustique des pistons rigides dans son livre "THEORY OF SOUND".Pour revenir à la modélisation, on part d'un signal électrique (délivré par l'amplificateur), ce signal électrique (c'est la première transformation) est d'abord converti en un mouvement de la membrane grâce au moteur (cette conversion a généralement un bon rendement).
La membrane émet par son mouvement alternatif une onde acoustique dans l'air ambiant, c'est la deuxième transformation.
Cette deuxième transformation est généralement d'un rendement faible puisqu'on parle pour une enceinte close d'un rendement maximal de 3%.L'idée essentielle de la modélisation (en s'appuyant sur les analogies électromécaniques et acoustiques d'Olson et de Beranek) c'est de ramener l'étude des phénomènes électriques, mécaniques et acoustiques à un seul schéma électrique unifié et équivalent (travaux de THIELE et SMALL).
Quelque chose d'un peu compliqué au départ se transforme ainsi en l'étude d'un banal filtre électrique passe-haut composé de résistances R, d'inductances L, et de capacités C.
On sait parfaitement résoudre ce genre de problème grâce à la théorie des filtres.
L'étude des filtres
Un haut-parleur nu ou un haut-parleur monté dans un coffret ont un comportement en fréquence qui correspond à celui d'un filtre passe-haut d'ordre 2.
C'est la même chose que la capacité en série et l'inductance en parallèle que l'on utilise pour composer le filtre passe-haut qui va attaquer un médium ou un tweeter dont on suppose l'impédance constante de valeur R (Ohm).On peut expliciter la fonction de transfert normalisée de ce type de filtres électriques suivant deux types de modélisation.
Première modélisation :
La première manière pour résoudre ce problème de filtre consiste à poser :
LC w02 = 1.
Q = Lw0 / R.
w / w0 = x.
Tout calcul fait on aboutit à une fonction de transfert T(x) dont l'expression mathématique est la suivante:
T(x) = x2 / (1 + ((1 - 2Q2) / Q2)x2 + x4)0,5.
Q est appelé facteur de surtension ou encore facteur de qualité.C'est donc x2 au numérateur divisé par la racine carrée d'une fonction F(x) de degré 4.
La racine carrée de quatre étant deux, le dénominateur est donc une fonction de degré 2.F(x) = [1 + ((1 - 2Q2) / Q2)x2 + x4]0,5
Cette fonction F(x), selon les valeurs que prend le paramètre Q, peut être une fonction de Butterworth notée B2 (Q = 0,707), une fonction de Chebychev 0,1dB (Q=???), de Chebychev 0,5 dB (Q = ???), une fonction de Bessel (Q = 0,577), etc., d'ou le nom des charges acoustiques les plus classiquement utilisées.
Cette première manière est un peu compliquée par sa formulation, mais est intéressante si on veut par exemple tracer sur un tableur les courbes de réponse en fréquence en fonction du rapport w /w0) où si l'on préfère (f / f0)
On trace généralement ces courbes pour les valeurs classiques de Q, à savoir 1 / 2, 1 / racine(2), 1 / racine(2) / 2. (voir annexe).
Deuxième modélisation :
La deuxième méthode consiste à adopter la notation utilisée pour les nombres complexes en posant p = j avec j le nombre imaginaire dont le carré est égal à -1 (j2 = -1
On l'appelle i en mathématique, mais les physiciens en électronique l'ont toujours appelé j.
Parce que le i des mathématiciens risque d'être confondu avec le i du courant...Tout calcul fait, on arrive à l'expression de la fonction de transfert normalisée (normalisée veut tout simplement dire que l'on se débrouille toujours pour avoir 1 comme facteur multiplicatif du terme de degré le plus élevé du polynôme apparaissant au dénominateur.
Dans notre cas, c'est-à-dire l'étude des filtres du deuxième ordre, c'est le coefficient devant le terme p2 que l'on doit rendre égal à 1 par une petite astuce mathématique simple).
L'expression de la fonction normalisée est la suivante : G(j/jo) = p2 / (1 + 1/Q * p + p2)C'est donc p2 divisé par la racine carrée d'un polynôme P(p) de degré 2, et dont l'expression mathématique est :
P(p) = 1 + 1 / Q * p + p2Ce polynôme P(p) n'est qu'une formulation alternative de la fonction F(x) précédente.
Il peut être un polynôme de Butterworth noté B2, un polynôme de Chebyshev 0,1dB noté T2 (k=0,1), Chebyshev 0,5 dB noté T2 (k=0,5), un polynôme de Bessel, noté B2, etc.
Ces familles de polynômes ont chacune leurs caractéristiques propres (pente de la coupure, déphasage, rotation de phase, réponse aux impulsions, etc.) donc des avantages et des inconvénients.Pour les filtres de séparations des voies d'une enceinte, on utilise le plus couramment des filtres de type Butterworth, et des filtres de Linkwitz-Riley (utilisant les polynômes de Linkwitz-Riley).
Il est d'ailleurs curieux que personne n'ait jamais avoué utiliser un filtre de type Linkwitz-Riley pour optimiser une charge de haut-parleur, ce type de filtre a pourtant d'évidentes qualités.
Il est souvent utilisé dans les filtres d'aiguillage des haut-parleurs qui composent une enceinte multivoie, même s'il ne correspond pas à la meilleure réponse de niveau dans les graves (encore une affaire de marketing ! ? quand on parle d'enceintes).Nota : pour les enceintes de type basse reflex le polynôme qui apparaît au dénominateur de la fonction de transfert normalisée est un polynôme de degré 4, d'où les appellations B4, T4, QB3, HM39, HM50, etc.
Valeurs de Q en fonction du polynôme choisi :
| Type de réponse | Notation | Valeur de Q |
|---|---|---|
| Linkwitz-Riley | LR 2 | 0,500 |
| Bessel | D | 0,577 |
| Butterworth | B2 | 0,707 |
Pour un coffret clos, si on s'arrange pour obtenir un Qtc = 1,1, on démontre mathématiquement que cela correspond au rendement maximal et à la puissance maximale que peut produire un haut-parleur monté dans un coffret clos (voir COURBE2).
Le pic de réponse dans les basses n'est pas trop important (<2dB).On ne peut pas choisir n'importe quel haut-parleur pour concevoir une enceinte close.
Le haut-parleur doit posséder un Vas suffisamment grand, et un Qts pas trop faible pour ne pas tomber dans des volumes d'enceintes Vb trop petits.
En principe pour faire une enceinte close, on choisit un haut-parleur tel que Fs / Qes < 50.
Ne pas trop s'inquiéter (sauf si vous avez déjà acheté les deux haut-parleurs), le calcul pratique ci-après vous donnera des résultats impossibles ou peu raisonnables si le Haut-parleur n'est pas adapté à une charge close (les constructeurs sérieux indiquent le type d'utilisation des haut-parleurs).
Calcul d'une enceinte close
On connaît les paramètres Fs, Qts, Cms (où Vas) du haut-parleur
On choisit le Qtc que l'on souhaite toujours supérieur à Qts ( 0,5 < Qtc < 2 généralement ).
On calcule a = ( Qtc / Qts )2 - 1
On calcule le volume intérieur de l'enceinte Vb = Vas / aVb est le volume de calcul.
Le volume à réaliser en pratique sera un peu plus faible, car il faut tenir compte du volume de l'absorbant placé à l'intérieur.
Si l'on considère que l'on met 15% du volume Vb en absorbant (il ne faut pas en mettre de trop pour ne pas étouffer le son), et puisque l'absorbant augmente le volume virtuel de l'enceinte de 20% de son volume, le volume pratique de l'enceinte est :
Vb - 0.15 * Vb * 0.2 = Vb * ( 1 - 0.15 * 0.20 ) = Vb * 0.97.
Ce sont les valeurs par défaut lors des calculs effectués en base de données, si ce n'est que vous pouvez changer vous-même le volume de l'absorbant utilisé.Pour rappel, si les données du constructeur ne donnent pas le Vas :
Vas = C2 * Ro * Cms * Sd2, avec C = 343.707 m/s et Ro = 1.194 kg/m3 à 20°C, 50 m d'altitude et 40% d'humidité relative.La fréquence de résonance du haut-parleur dans son coffret Fc est donnée par
Fc = Fs * ( Vas / Vb + 1 )0.5
La fréquence Fc est toujours supérieure à Fs, ce qui est intuitif.
Que l'on peut écrire aussi avec a, soit Fc = Fs * ( a + 1 )0.5La fréquence de coupure à mi-puissance vaut :
F-3dB = F3 = Fc * racine[ ( Qtc-2 - 2 + racine[ ( Qtc-2 - 2 )2 + 4 ) ] / 2 ]En PHP :
$f3 = $fc*sqrt((pow($qtc,-2)-2+sqrt(pow(pow($qtc,-2)-2,2)+4))/2);
C'est la formule utilisée telle quelle dans la base de données, j'ai eu du mal à la rentrer correctement.
Je vous garantis l'exactitude de cette formule écrite en PHP, c'est la formule 9.85 du livre de Mario ROSSI.Si on pose A = ( 1 / Qtc2 ) -2
Alors F-3dB = F3 = Fc * racine[ ( A + racine[ A2 + 4 ] ) / 2 ]La valeur du pic en dB (il n'existe que si Qtc > 0,707) de la réponse dans le grave se calcule ainsi :
Pic dB = 10 * LOG [ Qtc4 / ( Qtc2 - 0,25 ) ]Ce pic correspond à la fréquence Fpic = [ 1 / (1 - 1 / 2 / Qtc2 )0.5 ] * Fc
Phase acoustique
Quel que soit le Qtc de l'enceinte close, la phase acoustique passe par 90° à Fc.
C'est un moyen très simple de vérification pour vérifier si votre mesure est bonne ou pas :
Une mesure de la courbe d'impédance pour relever Fc là où la phase électrique passe par 0° et où l'impédance est maximum.
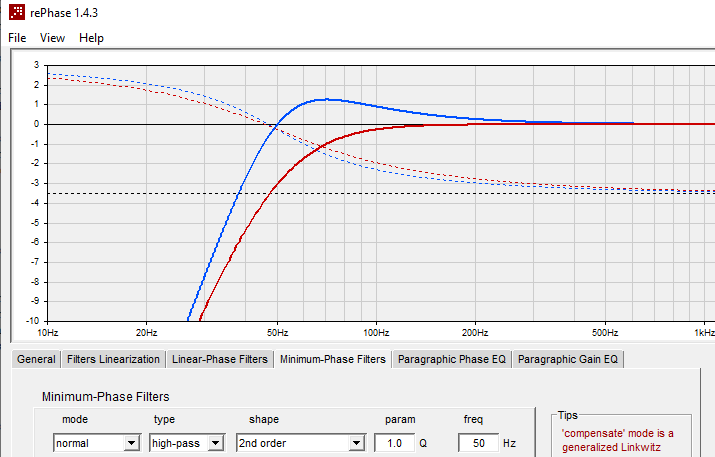
Une mesure de la courbe de réponse avec la phase acoustique (pas la phase minimum ni l'excess phase) pour vérifier les 90° environ à Fc.En images, deux enceintes closes, images faites avec rePhase :
Bleu : Fc = 50 Hz, Qtc = 1.000, 0.00 dB à 50 Hz.
Rouge : Fc = 50 Hz, Qtc = 0.707, -3.0 dB à 50 Hz.
Dans les deux cas, la phase acoustique passe à +90° à 50 Hz.L'atténuation à Fc c'est 20 * LOG( Qtc ).
-0.00 dB pour Qtc = 1.000.
-3.01 dB pour Qtc = 0.707 (Butterworth).
-4.78 dB pour Qtc = 0.577 (Bessel).
-6.02 dB pour Qtc = 0.500 (Linkwitz-Riley).
Construction d'une enceinte close
Le volume de l'enceinte close étant calculé, il ne reste plus qu'à construire le coffret dont le volume net intérieur sera égal à Vb.
Il faut en effet tenir compte des volumes pris à l'intérieur de l'enceinte par la partie arrière du haut-parleur, ainsi que tous les autres dispositifs qui se trouvent dans le coffret (filtre de séparation, bornes encastrées pour le raccordement à l'amplificateur, tasseaux de renforcement, etc.).D'après la théorie, la forme extérieure idéale pour un tel coffret serait la sphère, mais celle-ci est de construction difficile.
Si le choix se porte vers un parallélépipède, il faut absolument éviter la forme d'un cube, celui-ci étant générateur par sa parfaite symétrie de modes propres de vibration des ondes acoustiques à l'intérieur du coffret qui polluent le son émit par la face avant de la membrane.
À ce sujet il ne faut jamais oublier qu'une membrane de haut-parleur est transparente d'un point de vue acoustique.
Avec le désavantage d'une construction plus difficile, il vaut mieux privilégier les parois non parallèles.Pour la construction d'un coffret parallélépipédique, il faut choisir de bonnes proportions.
Le tableau ci-après donne quelques proportions jugées bonnes de manière empirique et pour le point de vue acoustique.
Le lien sur le chapitre proportion va beaucoup plus loin.
| X | Y | Z |
|---|---|---|
| 1.000 | 1,202 | 1,435 |
| 1.000 | 1,260 | 1,587 |
| 1.000 | 1,401 | 1,863 |
Pour l'amortissement, on utilise de la laine naturelle, minérale, de la mousse synthétique.
La laine de verre n'est pas recommandée à cause de ses effets sur la santé avec des microparticules irritantes que l'on peut inhaler.Les parois de l'enceinte doivent être les plus rigides possibles et ceci même pour les petits coffrets.
On peut percer un petit trou pour permettre la décompression du volume intérieur et avoir une pression statique à l'intérieur du coffret égale à celle de l'air ambiant.La mesure de l'impédance du haut-parleur monté dans l'enceinte permettra de vérifier que les calculs et la construction ont été bien menés (mesure de Fc et de Qtc).
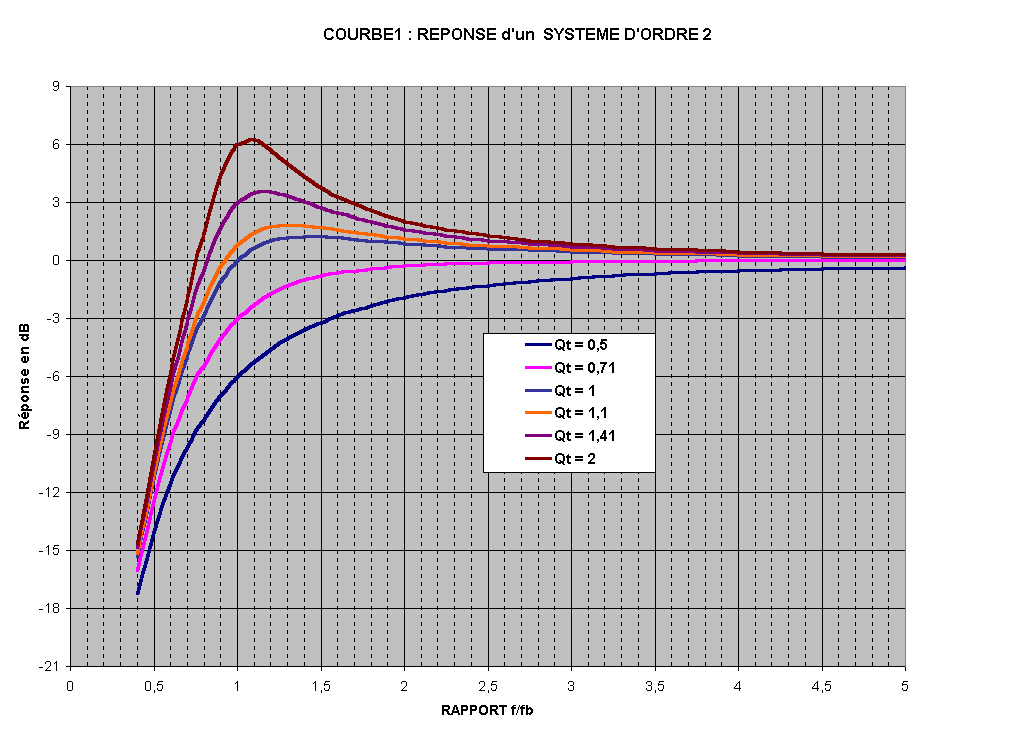
Courbe N°1
Ce sont les courbes classiques que l'on voit sur tous les livres traitant d'enceintes acoustiques.
Le rapport F / Fc vaut 1 quand la valeur de F est égale à celle de Fc.
Je n'aime absolument pas cette courbe qui est trop théorique, et je préfère de loin la courbe N°3.Les différentes courbes que l'on voit correspondent chacune à un haut-parleur théorique différent chaque fois du précédent ou du suivant.
Tous ces haut-parleurs ont une seule caractéristique commune, la fréquence de résonance Fc du système (haut-parleur + coffret) est chaque fois identique, et ce pour chaque valeur de Qtc.Dans la réalité pour un seul et même haut-parleur, les courbes de réponse se déplacent vers la droite du graphique quand le Qtc augmente.
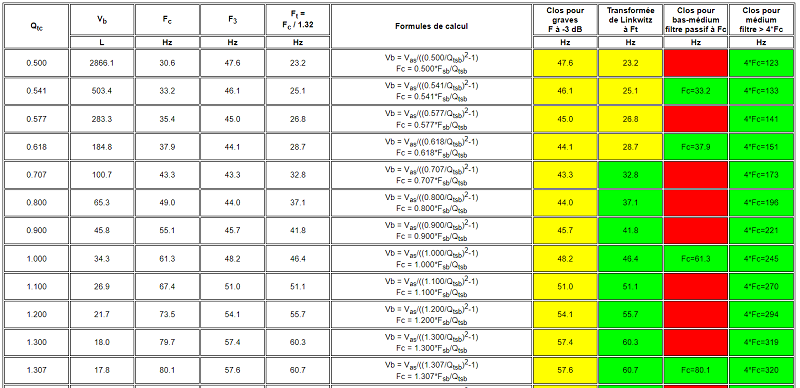
En effet, voir la formule de calcul, la fréquence de résonance Fc augmente avec Qtc, voir la courbe 2.Tableau général pour quelques valeurs de Qtc :
| Paramètre | unité | Q < 20.5/2 | Q > 20.5/2 | ||||
|---|---|---|---|---|---|---|---|
| Qtc | 0,50 | 0,71 | 1,00 | 1,10 | 1,41 | 2,00 | |
| F à -3 dB / Fc | 1,554 | 1,000 | 0,786 | 0,757 | 0,707 | 0,674 | |
| Réponse à Fc | dB | -6,00 | -3,00 | 0,00 | 0,20 | 3,00 | 6,00 |
| Pic dB | dB | --- | --- | 1,25 | 1,83 | 3,59 | 6,30 |
| Fpic / Fc | dB | --- | --- | 1,41 | 1,31 | 1,15 | 1,07 |
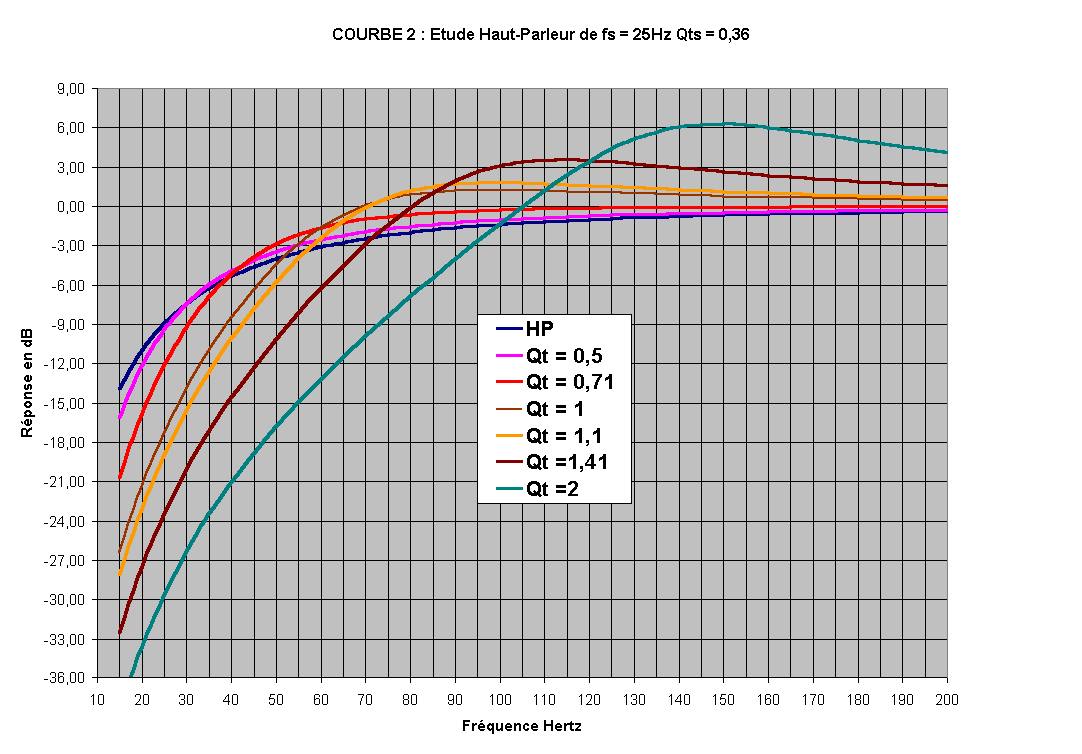
Courbe N°2
Toutes les courbes en fonction de Qtc ont été tracées pour un seul et même haut-parleur dont la fréquence de résonance est Fs = 25 Hz et Qts = 0,36.
Par rapport au graphique précédent, on voit bien le décalage des courbes vers la droite avec l'augmentation de Qtc.Le tableau ci-dessous résume les valeurs de Fc et de F à -3 dB en fonction du Qtc choisi.
| Qtc | Alpha | Fc | F à -3 dB |
|---|---|---|---|
| 0,50 | 0,9290 | 34,7 | 54,0 |
| 0,71 | 2,8580 | 49,1 | 49,1 |
| 1.00 | 6,7160 | 69,4 | 54,6 |
| 1,10 | 8,3364 | 76,4 | 57,8 |
| 1,41 | 14,4321 | 98,2 | 69,4 |
| 2.00 | 29,8642 | 138,9 | 93,6 |
Ce tableau est intéressant, car il montre bien qu'avec l'augmentation de Qtc, il y aussi une augmentation de la fréquence de résonance Fc du système :
Pour Qtc = 0,5, on a Fc = 34,5 Hz, pour Qtc = 2, on a Fc = 138,9 Hz.Si on me demandait mon avis, je choisirais pour cet exemple un Qtc de 0,5 qui donne une réponse de l'enceinte très voisine de celle du haut-parleur monté dans un écran.
Cette valeur correspond à une réponse de type Linkwitz Riley.
Cette charge correspond aussi au volume d'enceinte le plus grand.
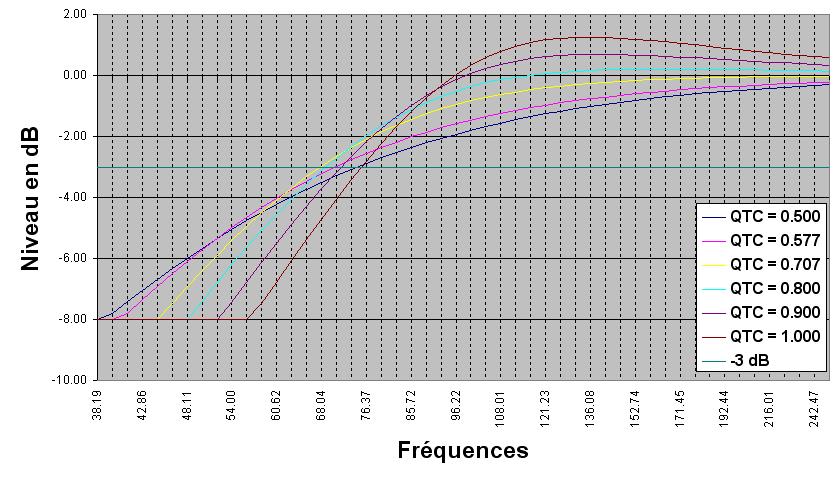
Courbe N°3
C'est la même chose que la courbe numéro 2, avec un peu plus de réalisme sur les échelles et les plages de Qtc.
Le haut-parleur est le BEYMA 10BR60. Fs = 45 Hz, Vas = 47 L, Qts = 0.467, Fs/Qes = 72.1 Hz, c'est un haut-parleur qui convient bien en clos.
Qtc = 0.500 ==> 343.2 L
Qtc = 0.577 ==> 92.4 L
Qtc = 0.707 ==> 37.1 L
Qtc = 0.800 ==> 24.7 L
Qtc = 0.900 ==> 17.6 L
Qtc = 1.000 ==> 13.3 LSi vous coupez les décibels en quatre, c'est la courbe jaune avec un Qtc de 0.707 que vous retiendrez pour la réponse à -3 dB.
Si vous intégrez l'énergie totale dans le grave, vous remarquerez que les courbes avec Qtc = 0.500 et Qtc = 0.577 ont plus de niveaux en dessous de -5 dB que la courbe avec un Qtc de 0.707.
L'amortissement optimal est obtenu pour le Qtc = 0.577, c'est un alignement de BESSEL.
Avec un QTC élevé : 1.414
Suite à une question posée sur un forum aujourd'hui fermé, voici des solutions de filtrage simples et élégantes :
Vous adoptez comme fréquence de répartition la fréquence de résonance Fc du HP dans son enceinte close et ajustez le Qtc à 1.414.
Ces corrections sont à effectuer avec le filtre actif dans la voie qui pilote le HP et non pas avec l'égaliseur.
Solution I
Vous utilisez une égalisation "Bell", Fréquence = Fc, Gain = -9.0 dB, Q = 1.414, qui donne une fonction de transfert du HP clos égalisé semblable à celle d'un passe-haut 12 dB/octave, Qtc = 0.500.
La réponse du HP ainsi égalisé et filtré sera alors celle d'un 12 dB/octave Linkwitz-Riley à Fc.
Solution II
Vous utilisez une égalisation "Bell", Fréquence = Fc, Gain = -3.0 dB, Q = 1.414, qui donne une fonction de transfert du HP égalisé semblable à celle d'un passe-haut 12 dB/octave, QTC = 1.000.
Vous ajoutez en actif un filtre 6 dB/octave à la même fréquence de coupure.
La réponse du HP ainsi égalisé et filtré sera alors celle d'un 18 dB/octave Butterworth à Fc.
Solution III
Vous utilisez une égalisation "Bell", Fréquence = Fc, Gain = -6.0 dB, Q = 1.414, qui donne une fonction de transfert du HP clos égalisé semblable à celle d'un passe-haut 12 dB/octave, QTC = 0.707 (Butterworth)
Vous ajoutez en actif un filtre 12 dB/octave Butterworth à la même fréquence de coupure.
La réponse du Visaton ainsi égalisé et filtré sera alors celle d'un 24 dB/octave Linkwitz-Riley à Fc.
Note très importante :
Les indications de Q varient suivant les constructeurs, la même valeur ne donne pas la même courbe chez XTA que chez Yamaha ou BSS.
Ce sont celles utilisées par ces deux dernières marques que j'emploie, je n'ai pas pu vérifier si le DCX BEHRINGER s'y conformait.
Domaine d'utilisation d'un haut-parleur :
Avec la base de Données haut-parleurs :
Vous pouvez vérifier vous-même, quel que soit le PC que vous utilisez, le domaine d'utilisation de votre haut-parleur en enceinte close, et de façon plus générale dans tous les domaines d'utilisation du haut-parleur que vous avez.
L'image ci-dessous est pour le BEYMA 10BR60 V2. L'utilisation est idéale en enceinte close ou en 1/4 d'onde, beaucoup moins dans une enceinte à évent.
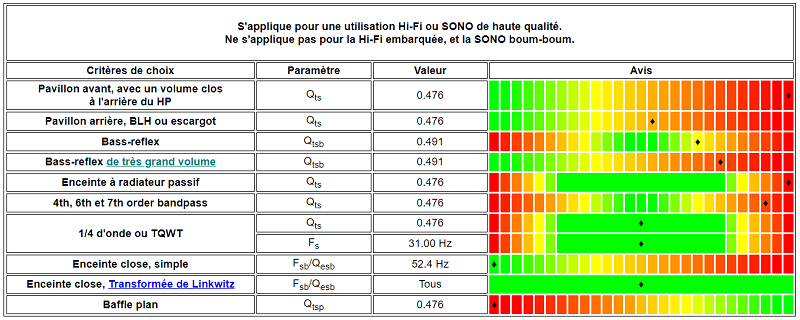
Ces indications éviteront bien des déboires aux débutants.
Un expert saura (peut-être) quand et pourquoi il peut passer outre, je ne passe pas outre, je n'ai pas à avoir de complaisance dans mes mails pour une utilisation bancale d'un haut-parleur...
Toutes les valeurs intermédiaires entre deux Qtc sont possibles, le tableau n'indique que quelques cas significatifs ou régulièrement répartis.La réponse dans le grave la plus étendue à 43 Hz à -3 dB est pour le Qtc de 0.707 dans un volume Vb de 100.7 Hz.
Vous pouvez avoir la même performance dans le grave avec une transformée de Linkwitz entre 35 à 45 L.
La transformée de Linkwitz se fait avec un égaliseur paramétrique ou par convolution.Si vous montez en enceinte close un haut-parleur inadapté, si vous le montez dans un volume franchement trop grand ou trop petit, je n'ai qu'un seul conseil à vous donner, arrêter le DIY...
Le calcul est fait directement par la base de données du site, vous affiche les tableaux ci-dessus en 3/6 et va jusqu'à l'affichage de la courbe de réponse en 4/6.
N'oubliez pas de rentrer la résistance du filtre passif en 2/6.
Le formulaire ci-dessous est rigoureusement le même que celui de la page 1/6 du calcul des enceintes closes.
Rechercher les haut-parleurs adaptés à votre enceinte close, 1/2 :
La recherche multicritère permet de trouver sur des critères objectifs les haut-parleurs qui répondent à votre demande.
C'est parmi les haut-parleurs de la liste obtenue avec des critères objectifs, que vous trouverez celui qui vous convient en le choisissant sur des critères subjectifs, de réputation ou de rendu à l'écoute.
Cette méthode est de loin préférable à un choix de haut-parleurs au petit bonheur la chance, c'est une exclusivité de ce site.
Notez que le séparateur décimal est le point, et non pas la virgule, dans toute la base de données.
Si vous devez rentrer 0.92 dans la case Qts, vous entrez : zéro, point, neuf, deux
Exemple de résultat d'une recherche :
Les données peuvent être triées sur chacun des paramètres.
Les valeurs de sélection sont indiquée au début de l'image.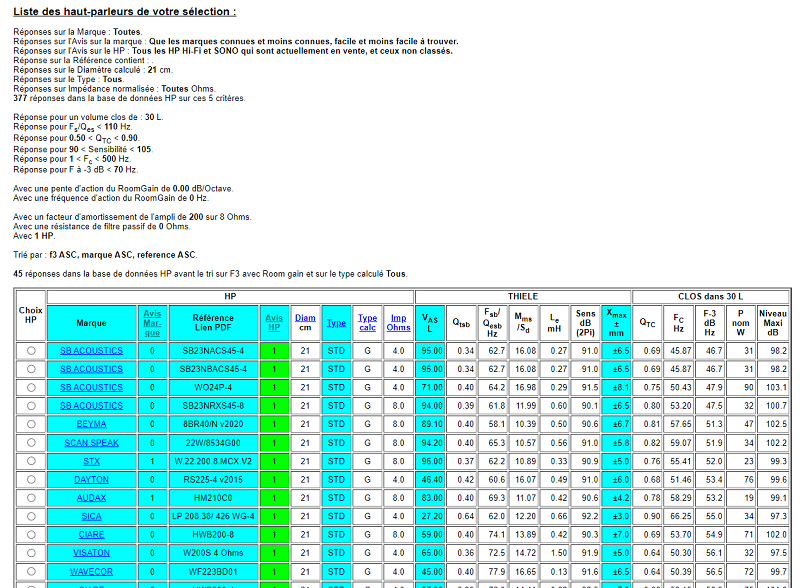
Un grand merci pour votre visite. --- Retour direct en haut de la page ---

Un grand-père facétieux disait à ses petits enfants que le grand truc blanc tout en haut du Puy-de-Dôme était un thermomètre géant.
Quand il deviendra tout rouge il faudra vite se sauver, parce que le volcan va se réveiller !!!Dôme Acoustique
Contrôle de validation W3C du code HTML 5 de la page, copiez l'adresse de la page avant de cliquer sur le lien.
Contrôle de validation W3C des CSS de la page, copiez l'adresse de la page avant de cliquer sur le lien.
Test "responsive" en simulant des écrans de smartphone de résolution différentes.
Ce sont trois outils de contrôle pour le webmaster du site Dôme Acoustique, c'est inutile pour les utilisateurs.
Avoir le lien dans chaque page est plus simple pour les retrouver.