| Page affichée à 12:36:26 samedi 21 décembre 2024 Ce site n'utilise pas de cookie |
 |
Dôme acoustique | Compteur pour tout le site : 17 184 152 Nombre actuel de lecteurs : 367 Les menus pour smartphone. |
Faire un don par PayPal |
| Le site de Dominique, un amateur passionné |
2-1-1-7 : Forme de l'évent
Mise à jour : 1 novembre 2024, Antimode 12.
Préambule :
Le calcul des évents se trouve sur deux chapitres :
- Calcul détaillé des évents : Calcul de l'évent.
- Calcul du diamètre équivalent à un évent circulaire pour les autres formes d'évent, uniquement dans le but de calculer le niveau SPL.
Dans ce chapitre, nous sommes dans la 2e partie.
Forme et nombre d'évents :
Pour les évents de grande surface, les tubes de grand diamètre sont difficiles à trouver.
Un ou plusieurs évents rectangulaires sont beaucoup plus faciles à réaliser dans ce cas et certainement beaucoup moins cher.
Attention cependant à la mise au point.On trouve facilement dans les grandes surfaces du bricolage des tubes en PVC en diamètre extérieur 4, 5, 6.3, 8, 10 et 12.5 cm, généralement en épaisseur 3.2 mm.
Avant d'acheter un évent chez votre vendeur de HP, regardez donc les prix...Votre vendeur vous dira qu'il vous vend un évent "réglable" et que mes (?) tubes PVC ne le sont pas.
Voyez un peu au chapitre mise au point la méthode du papier à dessin roulé... Convaincu ?
Évent rectangulaire :
José m'a envoyé plusieurs longs courriels très argumentés.
J'en ai fait des copier-coller conformément à la déontologie de ce site, avec l'accord de José.
1°) Diamètre équivalent, section équivalente et surface de contact équivalente
Vous écrivez :
Le diamètre de l'évent rond équivalent est : D = racine( 4 * S / Pi ) = racine( 4 * L * H / Pi ).
Avec le diamètre équivalent, tout ce qui est écrit plus haut dans ce chapitre s'applique aux évents rectangulaires.
À surface comparable, un évent rectangulaire et un évent rond ont rigoureusement la même profondeur.Le diamètre dont vous parlez est le diamètre pour lequel les deux évents auront la même section, puisque Pi * D^2 / 4 = L * H.
Certes, une même section garantit une même profondeur d'évent pour un accord donné.
Mais on se doute bien qu'un évent circulaire et un évent rectangulaire ne vont pas interagir de la même façon avec l'air.
Intéressons-nous en première approximation à la surface d'évent en contact avec l'air :
Pour un évent rond, cette surface est égale au périmètre fois la profondeur, soit Pi * D * P (P étant la profondeur) et pour un évent rectangulaire, cette surface est égale à (2L + 2H) * P.Exemple : Prenons trois évents de section rigoureusement identique.
- Évent 1 : carré, 20x20 cm, section = 400 cm2.
- Évent 2 : rectangulaire, 40x10 cm, section = 400 cm2.
- Évent 3 : circulaire de diamètre D = 22,6 cm, section : Pi * (22,6 / 2)^2 = 400 cm2.
Les périmètres sont les suivants : Périmètre 1 = 80 cm, Périmètre 2 = 100 cm et Périmètre 3 = 70,87 cm.
Au vu de ces périmètres, on voit bien qu'à section et profondeur d'évent identiques on va avoir, dans le cas des évents non circulaires, une plus grande surface de contact avec l'air.
Dans le cas d'un évent carré, cette surface est supérieure de 13% à celle de l'évent circulaire (80 / 70,87 = 1,13).
Dans le cas d'un évent rectangulaire, la surface va être encore supérieure au fur et à mesure que l'évent devient mince, donc que le rapport L / H devient grand.
Par ex. pour L / H = 4 (Évent 2), la surface est supérieure de 41% à celle de l'évent circulaire (100 / 70,87 = 1,41). Etc.On se doute bien que toute cette surface de contact supplémentaire va générer des frottements et que tout cela va avoir une influence.
Reste à approfondir la chose, car, jusqu'ici, on a seulement démontré qu'un évent de section carrée ou rectangulaire possède, à profondeur identique, plus de surface de contact avec l'air qu'un évent de section circulaire.
C'est déjà ça, mais ce n'est pas suffisant.
Poursuivons.
2°) Formule de Huesbscher et applications
Elle se trouve ici : http://membres.lycos.fr/depollunet/Precis/Chap3/Aspirat3c2_3.html et elle est employée dans le cite Francisaudio.
Elle est un peu barbare, mais enfin, la voici : Dh = 1,3 * [ (L * H)5 / (L + H)2 ](1/8)Cette formule de Huesbscher donne elle aussi un diamètre équivalent Dh.
Mais "équivalent" à quoi ?
En effet, ce n'est pas le diamètre permettant d'avoir une section équivalente ni un périmètre équivalent.
S'agit-il alors :
- Du diamètre isocinétique ?
Diamètre du conduit cylindrique engendrant la même VITESSE pour le même DÉBIT d'air.
- Du diamètre hydraulique ?
Diamètre du conduit cylindrique engendrant la même PERTE DE CHARGE LINÉAIRE pour la même VITESSE d'air).
- Du diamètre dit "équivalent" ?
Diamètre du conduit cylindrique engendrant la même PERTE DE CHARGE LINÉAIRE pour le même DÉBIT d'air.Pour info ces trois définitions viennent d'ici : http://www.mecaflux.com/diametres%20equivalents%20des%20conduits%20hydraulique%20aeraulique.htm
Si on en croit le site d'où est issue la formule, il s'agit en fait du diamètre hydraulique.
Voyons comment cela fonctionne sur un exemple.Prenons les mêmes 3 évents que précédemment et calculons les diamètres équivalents des deux premiers avec la formule de Huesbscher. On obtient :
Dh1 = 21,9 cm
Dh2 = 20,7 cm
On remarque que Dh1 et Dh2 sont inférieurs à D = 22,6 cm (on obtient toujours des diamètres inférieurs avec la formule de Huesbscher).
Mais qu'est-ce que cela signifie exactement ?Cela signifie que, pour une vitesse d'air donnée, (et pour une même profondeur d'évent), pour un évent circulaire de 21,9 cm de diamètre, on aura la même perte de charge que pour l'évent rectangulaire de 20x20 cm.
Et pour un évent circulaire de 20,7 cm de diamètre on aura la même perte de charge que pour l'évent rectangulaire de 40x10 cm.La perte de charge augmentant avec le diamètre, on voit bien que pour une vitesse d'air donnée, si on avait un évent circulaire de D = 22,6 cm, la perte de charge serait forcément supérieure que pour un évent rectangulaire de même section.
Donc, le débit d'air serait forcément inférieur.
Dit autrement, pour une vitesse maxi d'air donnée, à section équivalente, un évent circulaire admettra moins de débit d'air qu'un évent rectangulaire.
Dit autrement, pour une vitesse maxi d'air donnée, à débit admissible équivalent, un évent circulaire devra avoir une plus grande section qu'un évent rectangulaire.Reste à quantifier la "plus grande section", qui dépend bien sûr du rapport L x H de l'évent rectangulaire.
À partir de la formule de Huesbscher, il est facile de faire un petit tableau qui récapitule tout cela ( huesbscher.zip, 8 ko, puis huesbsher.xls sur votre PC ).
J'espère ne pas m'être trompé dans les calculs !
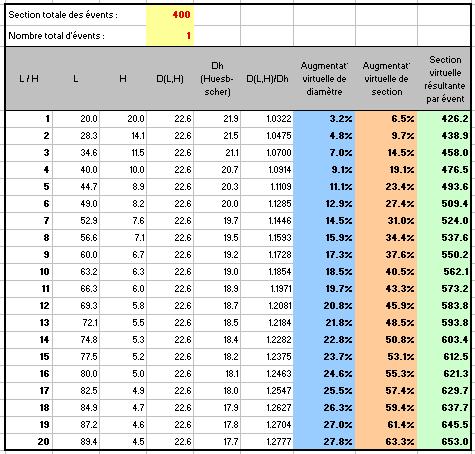
Que nous apprennent ce tableau et son graphique joint ?
Les colonnes intéressantes sont les colonnes bleues et rouges, qui correspondent aux courbes.
Ces colonnes montrent de combien il faudrait augmenter, respectivement, le diamètre et la section d'un évent circulaire pour avoir les mêmes performances que celles de l'évent rectangulaire dont il est question.
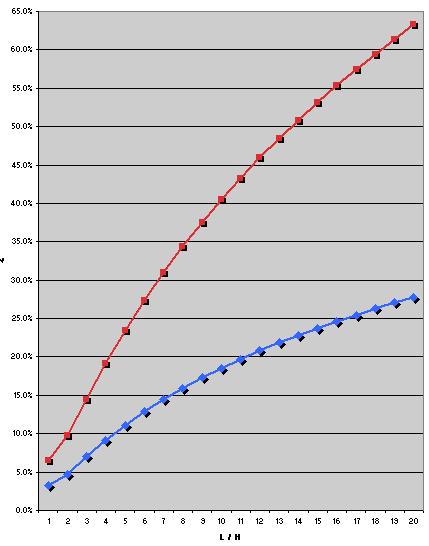
Par exemple, pour un ratio L / H de 4, on voit que l'évent rectangulaire se comporte du point de vue du débit admissible pour une vitesse maxi d'air donnée comme un évent circulaire virtuel dont le diamètre serait supérieur de 9.1% (soit une section supérieure de 19,1%).
Je vous ai même rajouté une ligne supplémentaire où vous pouvez rentrer le rapport L / H que vous souhaitez et calculer les colonnes bleues et rouges.
Vous pouvez intégrer très facilement les calculs de cette ligne dans votre propre calculateur d'évents !
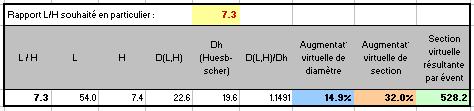
Ainsi, un utilisateur pourra entrer dans votre calculateur un évent rectangulaire donné, vous calculez le rapport L / H, vous en déduisez automatiquement la surface (forcément plus grande) de l'évent circulaire virtuel correspondant et vous l'utilisez pour la suite des calculs.
Facile non ?
Pour finir, quelques observations sur les courbes elles-mêmes :
- Pour un évent carré, le moins bon des cas, on a quand même une augmentation virtuelle de la section de 6,3% par rapport à un évent circulaire.
Je pense que la réalité doit être moindre (autour de 4-5%) si on extrapole la tendance dessinée par les courbes.
Ce qui me conduit à dire que la formule de Huesbscher n'est peut-être pleinement valable que pour L / H supérieur ou égal à 2.
- Pour un rapport L / H de 10, on est à 33,7% d'augmentation, c'est là que commence la définition des évents rectangulaires minces utilisée dans votre site.
- Tout cela pourrait sembler idéal, mais il ne faut pas oublier non plus qu'avec le rapport L / H on augmente aussi la surface d'évent en contact avec l'air.
Il faudra donc vérifier soigneusement que la surface en contact avec l'air ne dépasse pas la condition de l'évent de longueur maxi (cf. votre calculateur).
Précisions :
1°) Introduction :
Prenons le nombre de Reynolds http://fr.wikipedia.org/wiki/Nombre_de_Reynolds :
R = masse volumique * vitesse * diamètre (réel ou hydraulique) / viscosité dynamiqueLa masse volumique et la viscosité dynamique étant constantes pour ce qui nous occupe, le nombre de Reynolds est donc proportionnel à la vitesse fois le diamètre (réel ou hydraulique) :
On peut écrire R = n * V * D, n étant une constante.
2°) Raisonnement :
Soient plusieurs évents Ei définis par : leurs diamètres réels Di (si circulaires), leurs diamètres virtuels Dhi (si rectangulaires) et leurs sections réelles Si.
Soient autant d'écoulements dans les évents, définis par leurs nombres de Reynolds Ri.
- Pour un évent circulaire E1 (D1, S1), on a bien sûr R1 = n * V1 * D1.
- Pour un évent rectangulaire E2 (Dh2, S2), de même section réelle (S2 = S1), on calcule d'abord son diamètre virtuel de Huesbscher Dh2 (Dh2 < D1), puis on a R2 = n x V2 x Dh2.
Plaçons-nous pour commencer à vitesse identique (V1 = V2) :
Puisque Dh2 < D1, on a forcément R2 < R1.
Ce qui veut dire qu'avec une section réelle identique, et à débit identique, le niveau de turbulences est plus faible pour l'évent rectangulaire E2.
On s'en doutait bien.
Plaçons-nous maintenant à écoulement identique (R1 = R2) :
Donc V1 * D1 = V2 * Dh2.
Puisque Dh2 < D1, on a V2 > V1.
Cela veut dire qu'à section identique et pour un écoulement identique (nombre de Reynolds identique), un évent rectangulaire tolérera une plus grande vitesse qu'un évent circulaire.
Et comme les sections réelles sont identiques, une plus grande vitesse signifie un plus grand débit, donc un plus grand SPL.
On s'en doutait aussi.
Essayons de trouver maintenant le diamètre réel de l'évent circulaire E3 (D3, S3) :
Évent qui permettrait d'avoir le même SPL que l'évent rectangulaire E2, donc le même débit, toujours pour un écoulement identique (nombre de Reynolds identique, R2 = R3).
R2 = R3, donc V2 * Dh2 = V3 * D3.Ici les sections réelles ne sont plus identiques, mais on veut des débits identiques.
Donc S2 * V2 = S3 * V3 (égalité des débits)
Donc S3 = S2 * (V2 / V3)
Donc S3 = S2 * (D3 / Dh2)Or S3 = Pi * D32 /4
Donc Pi * D32 / 4 = S2 * D3 / Dh2
Donc D3 = S2 * 4 / (Pi * Dh2)
Or S2 = S1 = Pi * D12 / 4
Donc D3 = (Pi * D12 / 4) * (4 / (Pi * Dh2))Soit au final : D3 = D12 / Dh2.
Des valeurs à ne pas dépasser :
Un évent pour une enceinte idéale ne devrait pas dépasser un nombre de Reynolds de 20000, ce qui correspond à une vitesse de l'air dans l'évent de l'ordre de 5 m/s.
Vous aurez des problèmes si le nombre de Reynolds dépasse 50000.
Beaucoup d'enceintes ont des valeurs plus élevées, ce n'est pas bien du tout pour la qualité d'écoute.Le nombre de Reynolds est la valeur clef du bon dimensionnement d'un évent, quelle que soit sa forme.
Tests de validation :
Il faut reprendre la correction d'extrémité avec les évents rectangulaires :
Un évent qui touche le fond et les côtés n'a certainement pas la même correction d'extrémité qu'un évent rond qui arrive au milieu de l'enceinte.
Il y a une valeur spécifique pour le calcul des évents rectangulaire, Krect = 0.600, valeur qui ne pourra être affinée que lorsque j'aurai plus de valeurs tests.Le calcul de plusieurs évents rectangulaires utilise une petite astuce :
Un évent rectangulaire est assimilable a un évent circulaire via la formule de Huesbscher.
Deux évents rectangulaires deviennent donc deux évents circulaires avec un entraxe...
Un évent rectangulaire coupé en deux par un renfort se calcule comme s'il y avait 2 évents rectangulaires.Contrôle avec les outils "Quelle Longueur ?" et "Quel accord ?" dans le chapitre Calcul de l'évent.
- Quelle longueur, avec volume, accord mesuré, largeur, hauteur, nombre et entraxe.
- Quel accord, avec volume, largeur, hauteur, profondeur, nombre et entraxe.
| Valeurs tests | Valeurs calculées, K = 0.846 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Volume | Accord Mesuré |
Largeur | Hauteur | Profondeur | Position | Nombre | Entraxe | Accord | Profondeur |
| 106.74 L | 38.24 Hz | 31.0 cm | 7.2 cm | 26.2 cm | Bas | 1 | 0.0 cm | 39.47 Hz | 28.4 cm |
| 133.88 L | 32.30 Hz | 40.4 cm | 4.0 cm | 19.5 cm | Bas | 1 | 0.0 cm | 32.52 Hz | 19.8 cm |
| 145.00 L | 27.45 Hz | 40.0 cm | 5.5 cm | 40.0 cm | Bas | 1 | 0.0 cm | 27.30 Hz | 39.5 cm |
| 285.00 L | 39.10 Hz | 25.9 cm | 10 cm | 22.1 cm | Milieu | 2 | 27.7 cm | 39.05 Hz | 22.0 cm |
Le tableau ci-dessus n'a que 4 exemples, c'est trop peu.
Vous avez des exemples avec la fréquence d'accord mesurée de vos évents rectangulaires ?
Merci de m'envoyer vos résultats, plus j'aurai d'exemples, plus mes outils seront précis.
Si vos exemples sont avec des évents ronds, je ferai un autre tableau.
Plus il y aura d'exemples vérifiés, plus les outils de calculs seront précis.Le bon calcul d'évent est, pour moi, celui qui donne une profondeur un peu plus courte que ce qu'il faudrait réellement, car cela permet une mise au point à l'écoute en ajoutant un ou plusieurs tasseaux dans chacun des évents pour réduire la surface.
Il faut être réaliste, il ne sera pas possible d'avoir les valeurs exactes à tous les coups, il faut simplement s'en approcher d'assez près.
Essayez les valeurs tests dans d'autres logiciels, pour vous faire votre avis sur ce que je propose....La courbe d'impédance du premier exemple dans 106.74 L.
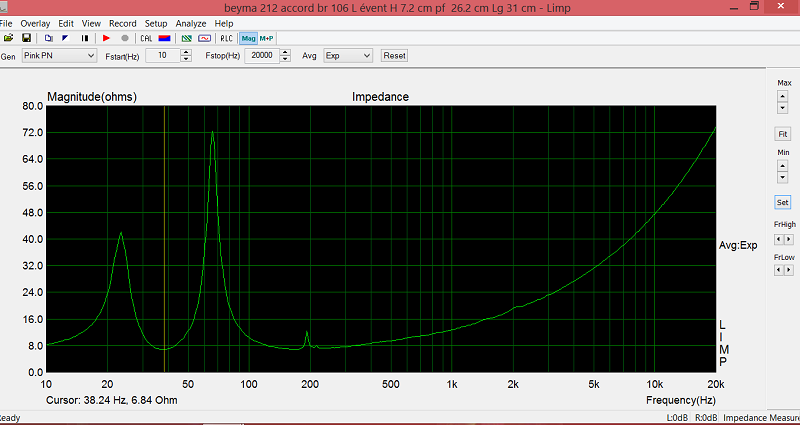
Évent "rectangulaire mince" :
Le point remarquable dans l'évent rectangulaire, défini par José ci-dessus, est que nous passons tout en douceur d'un évent carré à un évent rectangulaire, puis à un évent "rectangulaire mince", sans aucune rupture brutale de l'un à l'autre.
Je vous rappelle que la seule chose qui est laminaire dans un évent, par opposition à turbulent, c'est l'écoulement de l'air.
Un évent "laminaire", ça n'existe pas, c'est un évent rectangulaire mince...Un évent "laminaire" est un évent rectangulaire dont une dimension est petite devant les autres.
Par petit, il faut comprendre 7 à 10 fois plus petit (ou plus) que les autres dimensions.
Un évent de 22 x 4 cm de surface n'est pas un évent rectangulaire mince. ( 22 / 4 = 5.5 )
Un évent de 22 x 2.2 cm de surface est un évent rectangulaire mince. ( 22 / 2.2 = 10 )
Un évent de 22 x 1.5 cm de surface est un évent rectangulaire mince. ( 22 / 1.5 = 14.7 )À l'autre bout, un évent carré est un évent rectangulaire dont la largeur et la hauteur sont identiques.
L'évent rectangulaire mince se calcule comme un évent circulaire, avec la surface équivalente définie comme pour l'évent rectangulaire.
Le coefficient de correction change de façon continue, sans accident, en fonction du rapport largeur / hauteur.La mise au point à l'écoute d'un évent rectangulaire mince est indispensable, encore plus que pour les autres types d'évent.
S'il y a un effet de freinage de la lame d'air par les deux planches très proches, cet effet n'est pas intégré dans le calcul.
Comme un évent rectangulaire, un évent rectangulaire mince doit être réalisé trop grand et mis au point à l'écoute par réduction de la surface.
Le chapitre sur la mise au point.
Un évent "laminaire", ça n'existe pas !
Sur un forum, un internaute faisait remarquer qu'il n'y a pas d'évent "laminaire" !!!
Il n'y a que des évents rectangulaires avec un rapport largeur / hauteur plus ou moins grand...
Un évent "laminaire" n'est qu'un évent rectangulaire mince, ça fait tout de suite moins envie.Ce qui est laminaire, ou par opposition turbulent, c'est l'écoulement de l'air dans l'évent.
Il faut faire le maximum pour rester avec un écoulement laminaire de l'air dans l'évent, c'est-à-dire avec une vitesse de l'air dans l'évent aussi faible que possible vers 5 m/s, et un nombre de Reynolds idéalement <= 20000, et dans tous les cas < 50000.
Un évent rectangulaire mince, celui qui vous appelez à tort "laminaire", permet d'avoir plus facilement un nombre de Reynolds faible, c'est sa seule vertu.
Évent triangulaire :
Ces évents sont utiles sur les enceintes de SONO, ou sur les caissons de graves, avec 4 évents dans les 4 angles, pour une réalisation compacte plaquée contre le mur arrière.
Toujours José, à ma demande.
J'ai fait quelques recherches, mais je n'ai rien trouvé concernant les évents triangulaires.
Toutefois, rusons un peu :
On calcule facilement qu'un évent triangulaire rectangle a le même périmètre qu'un évent rectangulaire de rapport de dimensions L/H égal à 3,54645.
On pourrait donc dire (en première approximation bien sûr) qu'il se comporte "à peu de chose près" comme ce dernier pour l'écoulement de l'air.
Soit en utilisant mon tableur une augmentation virtuelle de section de 17,1% par rapport à un évent circulaire (en première approximation, je le répète, mais c'est mieux que rien et je pense qu'on n'est pas trop loin de la vérité).Les évents triangulaires rectangles sont donc a priori meilleurs que les évents circulaires, tout en étant inférieurs aux évents rectangulaires dont le rapport de dimensions commence à être supérieur à 4.
Certes ce raisonnement approximatif ne tient pas compte des angles fermés à 45° qui ont aussi une influence sur l'écoulement (résultant en une augmentation virtuelle de section légèrement supérieure à 17,1% en fait à mon avis), mais c'est mieux que rien.Voilà, en résumé, vous pourriez donc considérer dans votre tableau qu'un évent triangulaire rectangle se comporterait "à peu de chose près" comme un évent circulaire de section 17,1% supérieure (voire un tout petit peu plus).
Ou, ce qui reviendrait au même, le diamètre hydraulique d'un évent triangulaire rectangle serait égal au diamètre de l'évent circulaire de même section, multiplié par 0,924.Il y a une méthode qui marche à tous les coups, mesurer la courbe d'impédance pour avoir la fréquence d'accord au minimum entre les deux bosses, plus précisément là où la phase électrique passe par 0°.
Un évent très particulier :
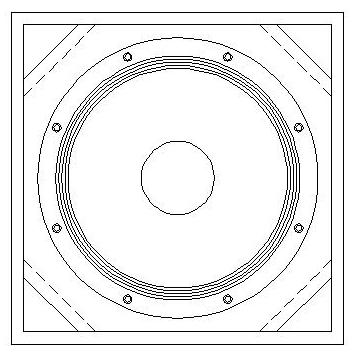
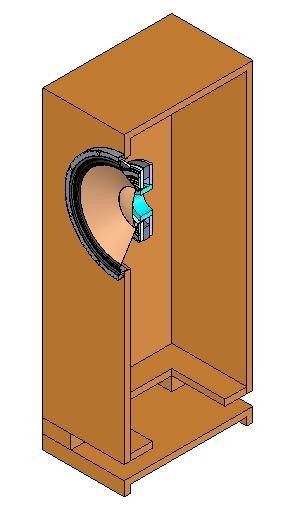 |
Comment modéliser l'évent ci-contre ?Un membre du forum, a réalisé une enceinte test de 160 L intérieurs, 45x45x80 intérieur, 49x49x84 extérieur, ouverture de 29x29, hauteur des pieds 10 cm. La fréquence d'accord a été mesurée avec ARTA LIMP à 55.1 Hz, et à pas grand-chose près, la courbe de phase passe à 0° à cette fréquence. |
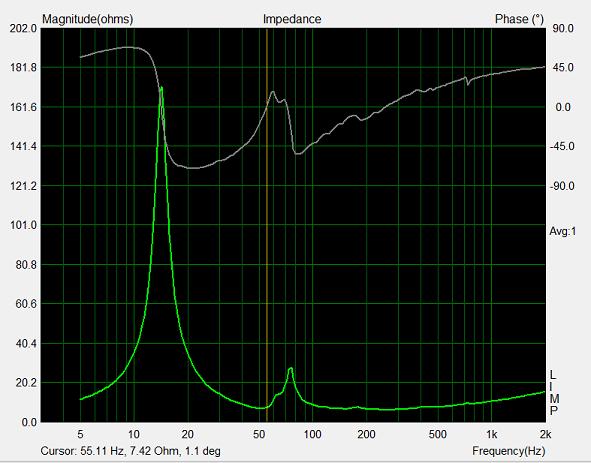
Plusieurs hypothèses de calculs ont été regardées pour modéliser cet évent :
- La première hypothèse, qui semble évidente lorsque les pieds sont haut, consiste à dire j'ai une ouverture de 29x29 cm, la planche fait 2 cm d'épaisseur.
L'accord calculé avec les outils du site est à 88.95 Hz, loin des 55.1 Hz.
- Une 2e hypothèse consiste à dire que le périmètre de l'évent est 29 + 29 + 29 + 29 = 116 cm, la hauteur fait 10 cm, la profondeur fait 10 cm.
L'accord calculé avec les outils du site est à 82.2 Hz, loin des 55.1 Hz.
Le diamètre Huesbscher est de 31.9 cm.
- Une 3e hypothèse consiste à dire que le périmètre de l'évent est 29 + 29 + 29 + 29 = 116 cm, la hauteur fait 10 cm, la profondeur fait 24.5 cm.
L'accord calculé avec les outils du site est à 63.9 Hz, pas si loin des 55.1 Hz.
Le diamètre de Huesbscher est de 31.9 cm.
- Une 4e hypothèse consiste à dire que le périmètre de l'évent est 29 + 29 + 29 + 29 = 116 cm, la hauteur fait 10 cm, la profondeur fait 26.5 cm.
L'accord calculé avec les outils du site est à 62.2 Hz, pas si loin des 55.1 Hz.
Le diamètre de Huesbscher est de 31.9 cm.
- Prenons les choses autrement, en calculant avec l'hypothèse d'un évent circulaire de 31.9 cm de diamètre, avec 160 L, et avec 55.1 Hz.
La longueur calculée est de 25.3 cm, pratiquement la demi-largeur de l'enceinte.C'est actuellement la meilleure hypothèse de calcul, qui demanderait à être vérifiée avec une hauteur des pieds moins haute, et/ou une ouverture d'une taille différente.
De toute façon, il faut toujours terminer un accord à l'écoute, et une précision du calcul a quelques Hertz près est largement suffisante.
Formulaire de calcul de l'évent RJ :
Évent tuyère :
Les études semblent sérieuses.
Les articles sur Internet semblent pertinents.Une société a été créée suite a ces études.
Des brevets ont été déposés.
Mais toujours aucun banc d'essai dans la presse.
Les liens ci-dessous ne sont que la preuve de mon intérêt, en aucun cas un avis technique sur la pertinence de cette solution.Mars 2016 : Deux liens, donc celui de la société créée pour vendre des enceintes avec un évent tuyère qui ne fonctionnent plus.
Je laisse celui qui fonctionne encore, et qui montre qu'à la condition de garder une vitesse de l'air raisonnable, l'évent tuyère n'apporte rien.
Un autre PDF sur le même sujet et au même endroit.
Un grand merci pour votre visite. --- Retour direct en haut de la page ---

Un grand-père facétieux disait à ses petits enfants que le grand truc blanc tout en haut du Puy-de-Dôme était un thermomètre géant.
Quand il deviendra tout rouge il faudra vite se sauver, parce que le volcan va se réveiller !!!
Dôme Acoustique
Contrôle de validation W3C du code HTML 5 de la page, copiez l'adresse de la page avant de cliquer sur le lien.
Contrôle de validation W3C des CSS de la page, copiez l'adresse de la page avant de cliquer sur le lien.
Test "responsive" en simulant des écrans de smartphone de résolution différentes.
Ce sont trois outils de contrôle pour le webmaster du site Dôme Acoustique, c'est inutile pour les utilisateurs.
Avoir le lien dans chaque page est plus simple pour les retrouver.