| Page affichée à 13:06:05 samedi 21 décembre 2024 Ce site n'utilise pas de cookie |
 |
Dôme acoustique | Compteur pour tout le site : 17 184 771 Nombre actuel de lecteurs : 397 Les menus pour smartphone. |
Faire un don par PayPal |
| Le site de Dominique, un amateur passionné |
2-6-6-3 : La correction d'impédance RLC en série
Mise à jour : 15 septembre 2024, Antidote 11.
Remarques :
Sous le terme RLC, il y a deux corrections complètement différentes :
- Il y a une correction "RLC en série", qui se branche en parallèle aux bornes d'un haut-parleur dans le but de linéariser la courbe d'impédance.
Cette correction est traitée ci-dessous.
- Il y a une correction "RLC en parallèle", qui se branche en série avec un haut-parleur dans le but de linéariser la courbe de réponse.
Cette correction n'est pas traitée dans ce chapitre.
Il y a trois cas de correction RLC en série :
- Pour un tweeter.
- Pour un haut-parleur sur un baffle plan.
- Pour un haut-parleur dans une enceinte close.
Si le premier ne se fait qu'à la mesure (au besoin celles fournies par le fabricant), les deux suivants peuvent se calculer facilement.
Pourquoi une correction RLC ?
Voici une simulation en bass-reflex :
En haut, la courbe d'impédance.
En bas, deux courbes de réponse, l'une sans filtre en bleu, l'autre avec un filtre à 6 dB en rose.
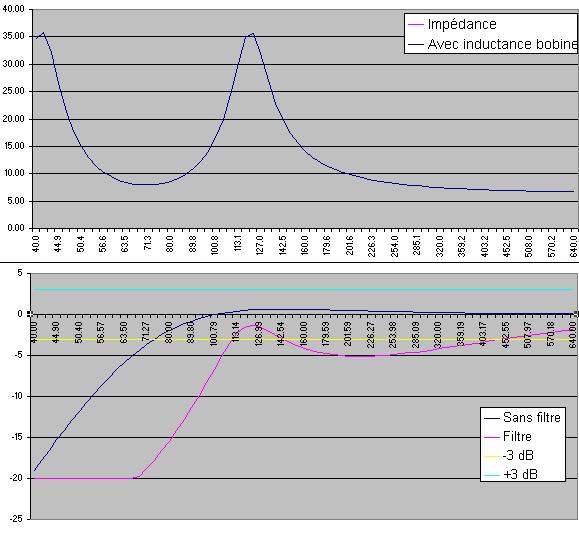
La courbe rose passe par -3 dB vers 450 Hz.
Si l'impédance était constante, cette courbe devrait passer par -7 dB à 225 Hz et par -12 dB à 110 Hz et -18 dB à 55 Hz.
Compte tenu de la remontée d'impédance, nous avons -5 dB à 225 Hz, et -1.5 dB à 110 Hz.
Le 55 Hz est à l'impédance théorique, car l'impédance est redescendue à une valeur "normale".
Le filtrage passif basse fréquence en passe-haut ne marche pas, à cause des variations d'impédance dans le grave.La solution, quand la charge le permet, est d'ajouter un RLC série en parallèle aux bornes du HP.
Les charges possibles sont l'enceinte close, l'enceinte infinie, le baffle plan, le pavillon.
Un tweeter est dans une enceinte close de très petit volume intégré au tweeter.L'enceinte bass-reflex ne peut pas être corrigée, car la courbe d'impédance a deux bosses, et donc il faut deux correcteurs d'impédance RLC en série, les deux correcteurs sont en parallèle.
Une grosse réserve :
En mai 2018 j'ai refait un test à l'écoute sur cette correction d'impédance RLC.
Le haut-parleur était un large bande DAVIS 20DE8 particulièrement performant, le cas était assimilable à une enceinte close.
La simple mesure de l'impédance m'a permis d'avoir Re, Zmax, Fs, Qms et Qes pour le calcul direct et sans erreur de la correction RLC, calcul avec le formulaire 1/2 vers la fin du chapitre.Première écoute en mono sur une enceinte, l'autre servait de référence : Gain de qualité à l'écoute dans le grave.
Installation de 2e correcteur sur l'autre enceinte et écoute plus prolongée sur 3 ou 4 jours, la dynamique du message sonore a baissé de façon sensible sur la mémoire auditive.
Nouveau test de comparaison à l'écoute en mono, en ayant retiré le correcteur RLC sur une des deux enceintes, sur des CD à forte dynamique.
Confirmation du petit gain sur le grave, et de la plus grosse perte de dynamique : J'ai retiré complètement les correcteurs RLC...Ce test ne concerne que la correction de l'impédance dans le grave, pas de celle d'un médium ou d'un tweeter.
C'est à vous de vérifier à l'écoute sur un médium ou un tweeter, si la suppression d'une bosse dans la courbe de réponse est plus importante qu'une baisse éventuelle de la dynamique que je n'ai pas revérifié à l'écoute.
Sur un haut-parleur de grave par contre, ne mettez pas de correcteur d'impédance RLC...N'oubliez pas qu'un filtre actif permet d'avoir le HP branché directement sur l'ampli sans le moindre composant passif.
Avec un mini DSP et des amplis FDA, ce ne sont pas des solutions chères.
RLC pour tweeter :
La correction d'impédance RLC série corrige aussi bien la bosse d'impédance de l'ensemble grave médium + tweeter + filtre que la bosse d'impédance d'un ensemble grave + médium + filtre.
Par abus de langage, nous parlerons dans la suite de grave médium et de tweeter.Le correcteur d'impédance RLC améliore grandement la qualité d'écoute.
Prenons un tweeter coupé à 6 dB sur 8 Ohms à 3000 Hz, et dont la dont la courbe d'impédance, de l'ensemble grave médium + tweeter + filtre, présente une bosse dont la valeur est de 32 Ohms à 750 Hz.
La capacité de filtrage sera C = 1 / 2 / Pi / 8 / 3000 = 6.6 uF.
À 3000 Hz, l'atténuation sera de 3 dB.
Avec une pente de 6 dB par octave nous avons -7 dB à 1500 Hz et -12.3 dB à 750 Hz.Calculons maintenant la fréquence de coupure avec les 32 Ohms de la bosse d'impédance.
F = 1 / 2 / Pi / 32 / 6.6E-6 = 750 Hz.
Nous avons donc, à la bosse d'impédance, une atténuation de -3 dB au lieu des -12.3 dB prévu.
L'écart est énorme et cela s'entend.
Les courbes ci-dessus sont assez éloquentes :Je remercie François pour les mesures effectuées sur son tweeter.
Le filtre utilisé :
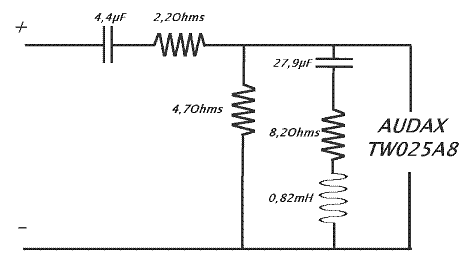
L'atténuation est de -5.8 dB sur 4.5 Ohms, la fréquence de coupure théorique est de 8045 Hz.
Les mesures :
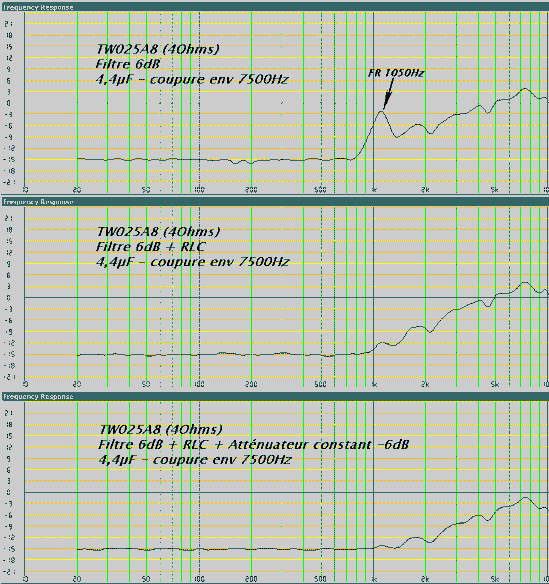
Le gain à 1200 Hz est parfaitement visible, il ne reste pratiquement plus de bosse due à la résonance du tweeter.
Un filtre à pente douce est une excellente chose, mais à condition de bien corriger les impédances pour faire fonctionner les filtres comme prévu par la théorie, avec une impédance constante.
Cette correction est le correcteur RLC.
RLC pour un haut-parleur sur baffle plan :
Nous avons les paramètres de base du haut-parleur à vide qui sont Re, Fs, Qms, Qes et Qts.
R6 = Re * ( 1 + Qes / Qms ) en Ohms
L6 = 1 / ( 2 * Pi ) * ( Qes * Re / Fs ) * 1000 en mH
C6 = 1 / ( 2 * Pi ) * ( 1 / ( Qes * Re * Fs ) ) * 1000000 en uF
Vérification :
Fc = racine( L6 / ( C6 /1000 ) ) / 2 / Pi / L6 * 1000 avec FC en Hz, L en mH et C en uFLa base de données haut-parleurs calcule directement les valeurs à utiliser, en demandant les données T&S du haut-parleur souhaité, et uniquement si le haut-parleur est utilisable sur un baffle plan.
Il y a un lien vers ce chapitre pour les explications.
Si le haut-parleur n'est pas utilisable en baffle plan, le tableau ne s'affiche pas.

RLC pour un haut-parleur en enceinte close :
De la même manière qu'il est possible de corriger l'impédance d'un haut-parleur sur baffle plan, il est possible de corriger l'impédance d'un HP monté en enceinte close.
La différence est dans les valeurs utilisées.
Si le baffle plan ne modifie pas (ou presque pas) les caractéristiques du haut-parleur données par le constructeur, l'enceinte close modifie la fréquence de résonance Fs en Fc, et les paramètres Qms en QMc, Qes en QEc et Qts en Qtc.Nous avons les paramètres de base du haut-parleur à vide qui sont Re, Fs, Qms, Qes, Qts et Vas.
Nous avons le paramètre de volume de l'enceinte close, Vc.Soit alpha = racine( ( Vas / Vc ) + 1 )
Fc = Fs * alpha
Qmc = Qms * alpha
Qec = Qes * alpha
Qtc = Qmc * Qec / ( Qmc + Qec )
Ce calcul est un calcul simplifié, donc non exact, mais très largement suffisant pour notre usage. Il est issu du livre de Mario ROSSI, AUDIO.R6 = Re * ( 1 + Qec / Qmc ) en Ohms
L6 = 1 / (2 * Pi ) * ( Qec * Re / Fc ) * 1000 en mH
C6 = 1 / ( 2 * Pi ) * ( 1 / ( Re * Qec * Fc ) ) * 1000000 en uF
Vérification :
Fc = racine( L6 / ( C6 /1000 ) ) / 2 / Pi / L6 * 1000 avec Fc en Hz, L en mH et C en uFL'outil de calcul des enceintes closes vous indique directement les R6, L6 et C6 à utiliser pour une enceinte close.
Les valeurs calculées dépendent du volume de l'enceinte close pour C6.
Il faut aller jusqu'au calcul de votre enceinte close pour avoir Fc.
Indiquez bien en page 2/6 que le Type de l'enceinte est "L'enceinte est de bas médium ou de médium : Grave filtré" pour avoir le tableau ci-dessous.
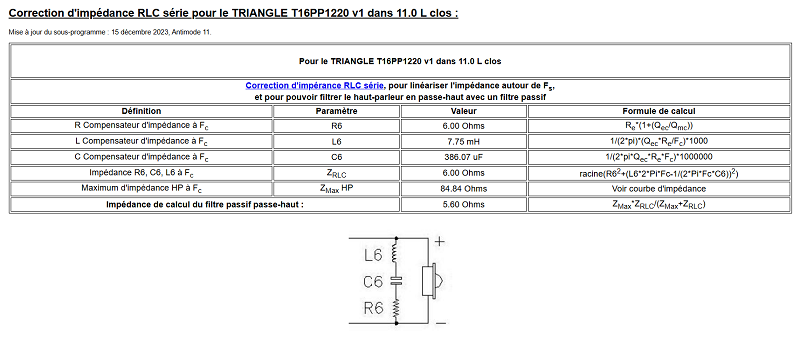
Une remarque :
À la fréquence Fc utilisée pour le calcul, le Zmax du haut-parleur et le Zrlc sont tous les deux purement résistifs.
Le calcul de l'impédance du filtre passif est donc possible à cette fréquence, sans tenir compte de la phase puisqu'elle est nulle.
Une fois corrigé, et comme le prouve les mesures, l'impédance est purement résistive de 20 Hz jusque 400 Hz environ.
Au-dessus de 400 Hz, un correcteur d'impédance RC est nécessaire.Une enceinte close, associée à un correcteur RLC et un filtre passif, est une excellente solution en bas médium, médium et aiguë.
Composants :
Les composants sont souvent de forte valeur, mais ne sont pas chers :
- Les outils de calculs du site choisissent une self Mundorf 071 avec un fil de 0.71 mm de diamètre de 0.40 mm2 de section, et de résistance au courant continu élevé (4.30 Ohms pour 15 mH).
- La valeur de R est celle de la résistance + la résistance interne de la self.
Si vous devez avoir 7.2 Ohms, et que votre self en fait 4.3, il faut ajouter une résistance de 7.2 - 4.3 = 2.9 Ohms.- La capacité sera chimique non polarisée, et découplée avec 2.2 uF de bonne qualité.
Composants de forte valeur :
Impédance d'un circuit RLC :
Calcul de l'impédance d'un circuit RLC à la fréquence F0 ou à la pulsation w0 = 2 * Pi * F0, avec R3 en Ohms, L3 en Henri, et C3 en Farad :
Z = racine( R32 + 1 / ( C3 * w0 )2 + ( L3 * w0 )2 )
Z = racine( R32 + 1 / ( C3 * 2 * Pi * F0 )2 + ( L3 * 2 * Pi * F0 )2 )
La résistance interne de la self est incluse dans la valeur de R3.
Mesures et calculs :
J'ai mesuré la courbe d'impédance d'un grave de 38 cm, et ai calculé les Fs, Qms, Qes et Qts du HP monté.
Cette courbe est en semi-clos, avec "un toit" sur le baffle plan.
En clos ou en vrai baffle plan, il n'y aurait qu'une seule bosse d'impédance).
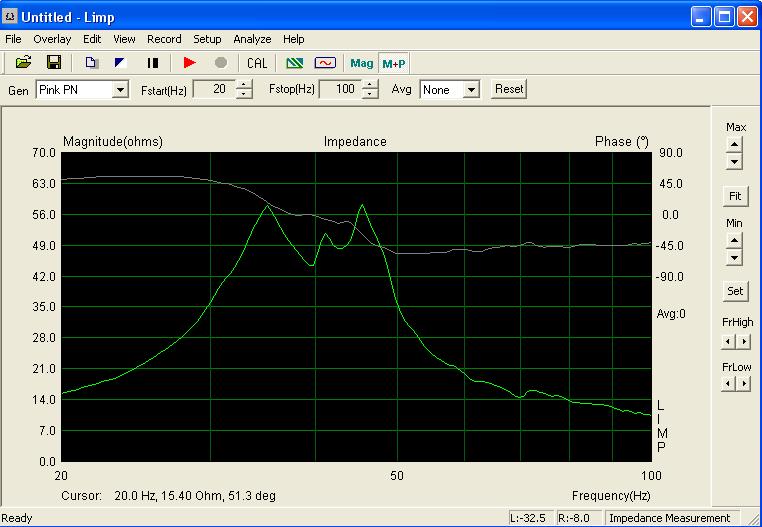
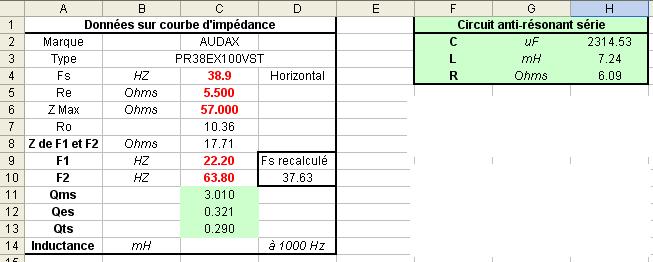
Avec ces valeurs, j'ai calculé le "RLC série" à placer en parallèle aux bornes du HP pour linéariser l'impédance.
Une fois les valeurs trouvées, le correcteur installé, j'ai remesuré l'impédance pour constater la linéarité.
Je ne vous cache pas que j'ai fait plusieurs fois les mesures avec et sans, sur les deux enceintes, en croyant a une erreur de mesure...
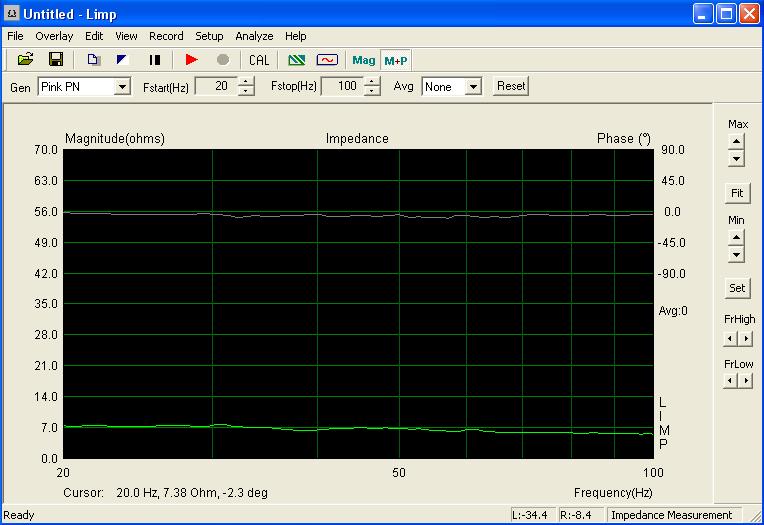
Si vous devez faire un filtre entre un grave et un large bande, avec une coupure basse, le RLC sur le grave et sur le large bande est indispensable.
Avec une courbe d'impédance aussi régulière, le filtre aura l'atténuation calculée.
Formulaire de calcul du correcteur RLC, 1/3
Pour tweeters et compressions, pour les autres HP, utilisez la base de données.
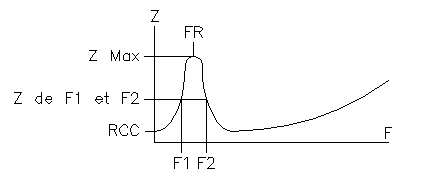
Vous devez avoir sous les yeux la courbe d'impédance du tweeter ou de la compression, pour relever sur la courbe les valeurs de Re, Zmax, F1 et F2.
La bosse dans la courbe d'impédance doit être unique.
| En 1/3, ci-dessous, vous devez rentrer Re et Zmax. En 2/3 la valeur de Z est calculée, et vous devez entrer F1 et F2. En 3/3 la valeur des composants du correcteur RLC, R6, C6 et L6 sont calculés. |
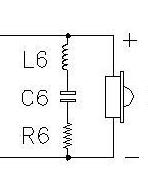 |
Notations : FR du schéma = Fs dans le texte. RCC du schéma = Re dans le texte. Le schéma sera modifié...
Formulaire de calcul du correcteur RLC, 1/2
Certains fabricants donnent pour leurs médiums ou leurs tweeters les paramètres de THIELE et SMALL dont Fs, Re, Qms et Qes.
Ces valeurs permettent de calculer directement le correcteur RLC, sans avoir besoin d'avoir la courbe d'impédance sous les yeux, sans avoir à interpréter la courbe pour en sortir des couples de points : Fréquence, Impédance.
Je vous conseille d'utiliser cette deuxième méthode chaque fois que c'est possible.
| En 1/2, ci-dessous, vous devez rentrer Fs, Re, Qms et Qes. En 2/2, la valeur des composants du correcteur RLC, R6, C6 et L6 sont calculés. |
 |
Les valeurs par défaut sont celles du médium MOREL EM 1308, car je les avais sous la main au moment de développer cette partie du calcul.
Une autre méthode :
Certains d'entre vous emploient un tweeter ou une compression avec une sensibilité très élevée, et mettent un atténuateur de 8 ou 10 dB pour égaliser les niveaux avec le médium ou le grave médium.
L'impédance de la compression ou du tweeter n'est pas toujours linéaire.
Si nous regardons l'impédance du tweeter et compression avec l'atténuateur L-PAD, les choses sont beaucoup mieux.Prenons un tweeter d'une impédance de 8 Ohms, avec un atténuateur de 10 dB, la résistance en série est 5.47 Ohms, celle en parallèle est 3.70 Ohms.
L'impédance vue par le filtre est 5.47 + ( 8.00 * 3.70 / ( 8.00 + 3.70 ) ) = 8.00 Ohms.
S'il y a une pointe d'impédance de 20 Ohms, l'impédance vue par le filtre est 5.47 + ( 20.00 * 3.70 / ( 20.00 + 3.70 ) ) = 8.59 Ohms.
Solution miracle ?
Non, car si vous calculez l'atténuation du L-PAD avec les 20 Ohms elle est de -8.79 dB au lieu des -10 dB souhaités.Refaisons le même calcul avec un atténuateur de 2 dB, la résistance en série est 1.65 Ohms, celle en parallèle est 30.90 Ohms.
L'impédance vue par le filtre est 1.65 + ( 8.00 * 30.90 / ( 8.00 + 30.90 ) ) = 8.00 Ohms.
S'il y a une pointe d'impédance de 20 Ohms, l'impédance vue par le filtre est 1.65 + ( 20.00 * 30.90 / ( 20.00 + 30.90 ) ) = 13.79 Ohms.
Moins efficace pour les faibles atténuations...
L'atténuation avec les 20 Ohms elle est de -1.11 dB au lieu des -2 dB souhaités.
Un grand merci pour votre visite. --- Retour direct en haut de la page ---

Un grand-père facétieux disait à ses petits enfants que le grand truc blanc tout en haut du Puy-de-Dôme était un thermomètre géant.
Quand il deviendra tout rouge il faudra vite se sauver, parce que le volcan va se réveiller !!!
Dôme Acoustique
Contrôle de validation W3C du code HTML 5 de la page, copiez l'adresse de la page avant de cliquer sur le lien.
Contrôle de validation W3C des CSS de la page, copiez l'adresse de la page avant de cliquer sur le lien.
Test "responsive" en simulant des écrans de smartphone de résolution différentes.
Ce sont trois outils de contrôle pour le webmaster du site Dôme Acoustique, c'est inutile pour les utilisateurs.
Avoir le lien dans chaque page est plus simple pour les retrouver.