| Page affichée à 12:51:08 samedi 21 décembre 2024 Ce site n'utilise pas de cookie |
 |
Dôme acoustique | Compteur pour tout le site : 17 184 450 Nombre actuel de lecteurs : 398 Les menus pour smartphone. |
Faire un don par PayPal |
| Le site de Dominique, un amateur passionné |
2-3-2-4 : Conception des pavillons JMLC
Mise à jour : 16 septembre 2023, Antidote 11.
Article trouvé dans la revue Musique et technique du 2e trimestre de 1999.
Cette revue a cessé de paraître depuis plusieurs années.
L'auteur, Jean Michel LE CLEAC'H, était bien connu sur plusieurs forums. Il est malheureusement décédé.La méthode de calcul a certainement évoluée depuis :
Contrairement au dessin de la page 4, ou les côtés du pavillon partent pratiquement horizontalement (à 90°), le calcul actuel montre des côtés qui repartent vers l'arrière (à 180°) pour revenir vers l'avant (270° et plus).
Page 1 / 5 :

Page 2 / 5 :

Page 3 / 5 :

Page 4 / 5 :
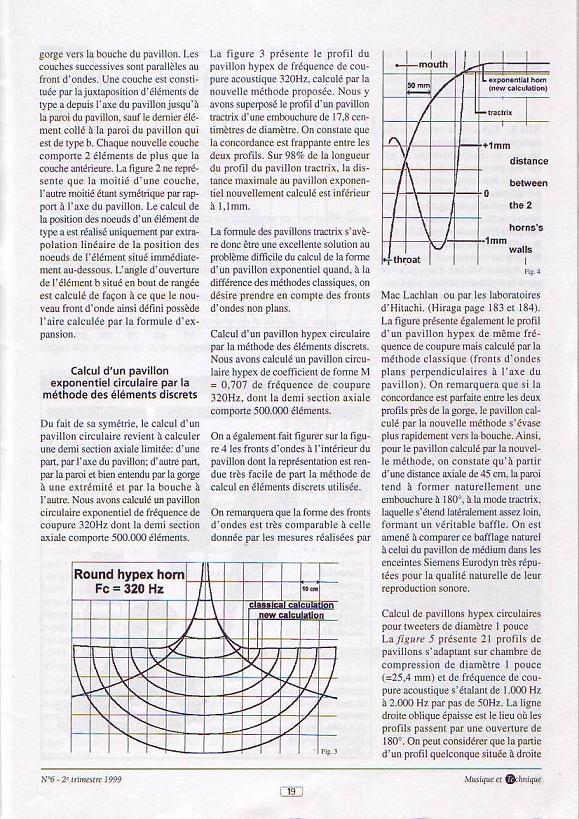
Page 5 / 5 :
Téléchargez la version 2007 du fichier de calcul de Jean Michel LE CLEAC'H.
C'est sur des points de détail comme celui-ci que l'on se rend compte combien Internet a fait des progrès au fil du temps.
Liens :
Calculateur de pavillon inspiré JMLC.
J'ai trouvé ce lien en cherchant "JMLC Like" dans un moteur de recherche.
Je le trouve intéressant pour son explication en couleur de la méthode de tracé à la CAO.
Base de calcul :
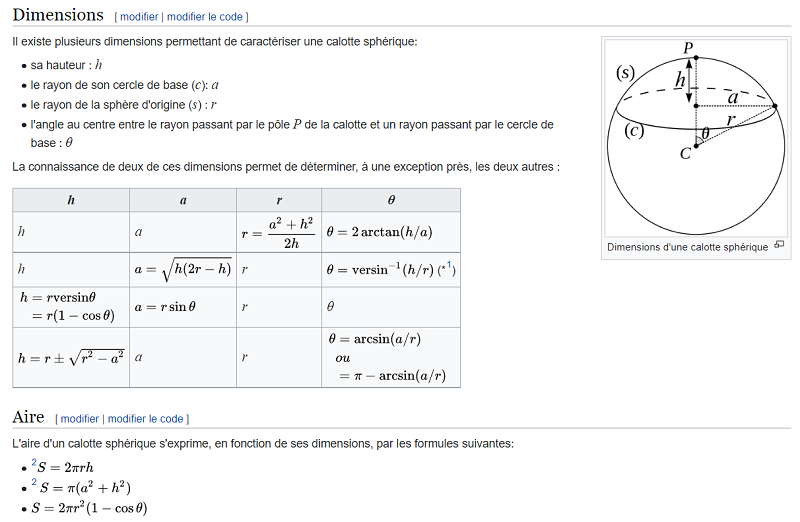
Calotte sphérique, pour le calcul de l'aire, dans Wikipédia.
Méthode de calcul Dôme Acoustique, départ du calcul :
Départ du calcul :
Les deux premières sections seront des sections sphériques.
La valeur de la première section sera conservée, la seconde à petite distance de la première ne sert qu'à avoir l'angle de départ du pavillon, angle qui ne dépend que de la surface de gorge, de la surface suivante à la distance X, et de la fréquence de calcul de la loi d'expansion.
Si la figure 2c montre des surfaces qui ont l'air droites, en pratique elles sont sphériques.
Si la même figure montre les sections F1, F2, F3, F4 et F5, je vais partir avec une section F0 de plus, F0 sera sphérique.Le calcul avec la loi d'expansion donne une surface S0 et une surface S1 à une distance X1 connue par rapport à S0.
Nous commencerons avec des surfaces planes de diamètre D0 = racine( S0 * 4 / Pi) et D1 = racine( S1 * 4 / Pi). R0 = D0 /2 et R1 = D1 / 2.
Ces deux diamètres permettent d'avoir l'angle de départ : ALPHA0 = ASIN( (R1 - R0) / X ).Avec l'angle, nous pouvons avoir le rayon de la première surface sphérique XDR0 = R0 / SIN( ALPHA0 ). Le point est souvent loin en arrière du départ du pavillon.
Nous pouvons aussi avoir H0 = XDR0 - racine( XDR02 - R02 ), et S0 = 2 * Pi * XDR0 * H0.Nous pouvons faire de même pour la surface 1 :
XDR1 = XDR0 + X1
H1 = XDR1 - racine( XDR12 - R12 ).
S1 = 2 * Pi * XDR1 * H1.
ALPHA1 = ALPHA0.L'aire d'une calotte sphérique est donnée avec 3 formules différentes, j'ai bien sûr calculé avec les 3 pour vérifier la cohérence jusqu'au 11e chiffre après la virgule.
Cette vérification faite, j'ai gardé la formule la plus simple...
Boucle d'ajustement :
Il faut retoucher les rayons R0 et R1 autant de fois que nécessaires pour faire correspondre les surfaces avec la loi d'expansion, et avoir l'angle de départ.
Nous avons un rayon R0, une surface théorique STH donnée par la loi d'expansion, une surface sphérique calculée SCALC.
Nouveau_R0 = R0 * racine( STH / SCALC ).
De la même façon, nous recalculons le nouveau R1.
Le calcul est relancé autant de fois que nécessaire, la différence entre ABS( STH - SCALC) est calculée, et quand la précision de 0.0000000001 mm2 est atteinte, le calcul est arrêté....
Fin du calcul :
Les valeurs R0 sont affichées dans le tableau.
La longueur de départ est 0 mm pour R0, la valeur est affichée elle aussi.
La longueur pour R1 est X * COS(ALPHA1).Nous avons maintenant de bonnes valeurs de départ pour calculer les autres sections.
Conclusion :
Le départ du calcul est vérifié et validé à une réserve près, il faut un très petit pas pour initialiser l'angle de départ avec une précision suffisante.
Je ne vous laisserai pas le choix de la valeur qui est initialisée à 0.005 mm !!!
Méthode de calcul Dôme Acoustique, autres surfaces :
Calcul de la surface d'un élément :
Les autres surfaces sont les éléments de type a et b en page 3/5.
Si nous définissons ces éléments avec un rayon, un angle de départ et un angle de fin, la surface F(i+1) pourra se calculer rigoureusement de la même façon pour les types a ou b.
L'élément de type b est nécessaire, c'est lui qui permettra d'obtenir la surface totale théorique en changeant progressivement l'angle par itérations.Imaginons que nous découpions chaque surface avec une toute petite longueur dL. dL = 0.0001 mm.
Avec le rayon R au milieu du dL, la circonférence est 2 * Pi * R, et la surface 2 * Pi * R * dL.
Une boucle de calcul fera la somme des surfaces de largeur dL sur la longueur L.
Mon calcul n'est pas un calcul exact, mais la vérification à la CAO donne une précision de 0.03 mm2 sur une portion de 10° à 1000 mm, précision que je n'arrive pas à réduire en gardant un temps de calcul encore raisonnable.
Il faudra voir la précision obtenue quand il y aura 20 ou 30 calculs de surfaces consécutifs, sur les grandes sections F20 à F30 éloignées de la gorge.
Surface d'ajustement :
C'est l'élément de type b en page 3/5 pour chacune des surfaces F1, F2, F3, F4, etc.
Les morceaux de surfaces de type a en page 3/5 sont connus, leur surface est calculable.
Une boucle permettra de trouver l'angle final à utiliser pour avoir la surface manquante.
Tronc de cône :
Soir R le grand rayon, r le petit rayon, h la hauteur, la surface S = Pi * (R + r) * a, avec a = racine(h2 + (R - r)2).
Aire d'un cône tronqué, méthode à creuser, ajoutée en septembre 2023...
Calcul d'une loi d'expansion :
| Fréquence de calcul de la loi d'expansion : 100.0 Hz, M = 3.6561 m-1, T = 0.707, C = 343.707 m/s. Fréquence minimale d'utilisation : 150.0 Hz pour le calcul du couple de valeurs (longueur, surface) pour N = 1, 2, 4 et 8. Pas de calcul = 50 mm, Pas d'affichage = 5 cm, Nombre de pas entre chaque affichage = 1. |
||||||
|---|---|---|---|---|---|---|
| COMMUN, LOI D'EXPANSION Surfaces à respecter quelque soit le type de surfaces : Plane, Cylindrique, Sphérique, JMLC, Temporelle ou Tractrix. |
ROND surfaces planes |
ROND surfaces JMLC J'abandonne pour quelques mois... |
||||
| N° | Longueur sur l'axe |
Surface | Diamètre | Longueur horizontale bord pavillon |
Verticale | 1/2 Angle |
| 0 | 0.00 cm | 150.0000 cm2 | 138.20 mm | |||
| 1 | 5.00 cm | 171.3796 cm2 | 147.72 mm | |||
| 2 | 10.00 cm | 197.2453 cm2 | 158.47 mm | |||
| 3 | 15.00 cm | 228.4639 cm2 | 170.55 mm | |||
| 4 | 20.00 cm | 266.0816 cm2 | 184.06 mm | |||
| 5 | 25.00 cm | 311.3590 cm2 | 199.11 mm | |||
| 6 | 30.00 cm | 365.8135 cm2 | 215.82 mm | |||
| 7 | 35.00 cm | 431.2697 cm2 | 234.33 mm | |||
| 8 | 40.00 cm | 509.9214 cm2 | 254.80 mm | |||
| 9 | 45.00 cm | 604.4041 cm2 | 277.41 mm | |||
| 10 | 50.00 cm | 717.8842 cm2 | 302.33 mm | |||
| 11 | 55.00 cm | 854.1645 cm2 | 329.78 mm | |||
| 12 | 60.00 cm | 1017.8120 cm2 | 359.99 mm | |||
| 13 | 65.00 cm | 1214.3107 cm2 | 393.21 mm | |||
| 14 | 70.00 cm | 1450.2456 cm2 | 429.71 mm | |||
| 15 | 75.00 cm | 1733.5231 cm2 | 469.81 mm | |||
| 16 | 80.00 cm | 2073.6362 cm2 | 513.83 mm | |||
| 17 | 85.00 cm | 2481.9827 cm2 | 562.15 mm | |||
| 18 | 90.00 cm | 2972.2468 cm2 | 615.17 mm | |||
| 19 | 95.00 cm | 3560.8578 cm2 | 673.34 mm | |||
| 20 | 100.00 cm | 4267.5410 cm2 | 737.13 mm | |||
| 21 | 105.00 cm | 5115.9782 cm2 | 807.09 mm | |||
| 22 | 110.00 cm | 6134.6018 cm2 | 883.79 mm | |||
| 23 | 115.00 cm | 7357.5472 cm2 | 967.88 mm | |||
| 24 | 120.00 cm | 8825.7970 cm2 | 1060.06 mm | |||
| 25 | 125.00 cm | 10588.5542 cm2 | 1161.11 mm | |||
| 26 | 130.00 cm | 12704.8912 cm2 | 1271.86 mm | |||
| 27 | 135.00 cm | 15245.7294 cm2 | 1393.25 mm | |||
| 28 | 140.00 cm | 18296.2157 cm2 | 1526.29 mm | |||
| 29 | 145.00 cm | 21958.5760 cm2 | 1672.08 mm | |||
| 30 | 150.00 cm | 26355.5412 cm2 | 1831.85 mm | |||
Un grand merci pour votre visite. --- Retour direct en haut de la page ---

Un grand-père facétieux disait à ses petits enfants que le grand truc blanc tout en haut du Puy-de-Dôme était un thermomètre géant.
Quand il deviendra tout rouge il faudra vite se sauver, parce que le volcan va se réveiller !!!
Dôme Acoustique
Contrôle de validation W3C du code HTML 5 de la page, copiez l'adresse de la page avant de cliquer sur le lien.
Contrôle de validation W3C des CSS de la page, copiez l'adresse de la page avant de cliquer sur le lien.
Test "responsive" en simulant des écrans de smartphone de résolution différentes.
Ce sont trois outils de contrôle pour le webmaster du site Dôme Acoustique, c'est inutile pour les utilisateurs.
Avoir le lien dans chaque page est plus simple pour les retrouver.