2-6-4-1 : Filtres série et parallèle, filtrage avec un haut-parleur relais

Mise à jour : 12 octobre 2023, Antidote 11.

 

Scan d'un article paru dans la Nouvelle Revue du SON, numéro 13 de décembre 1977, pages 127 à 130, sur le filtrage.
Si les formules de calculs des filtres de bases se trouvent dans tous les livres, les deux derniers filtres page 3 avec un haut-parleur relais ont un intérêt, c'est pourquoi vous trouvez ce scan.

Il faut noter que cette étude est basée sur des haut-parleurs parfaits, donc théoriquement purement résistifs avec une bande passante infinie, ce qui n'est jamais le cas en pratique.
C'est à ce niveau que se trouve l'explication du peu de succès pratique de cette solution de filtrage.

Les pages de l'article ont été annotées à la main, j'ai essayé de faire disparaître le plus possible de ces annotations.

 

Page 1/4 :

 

Page 2/4 :

 

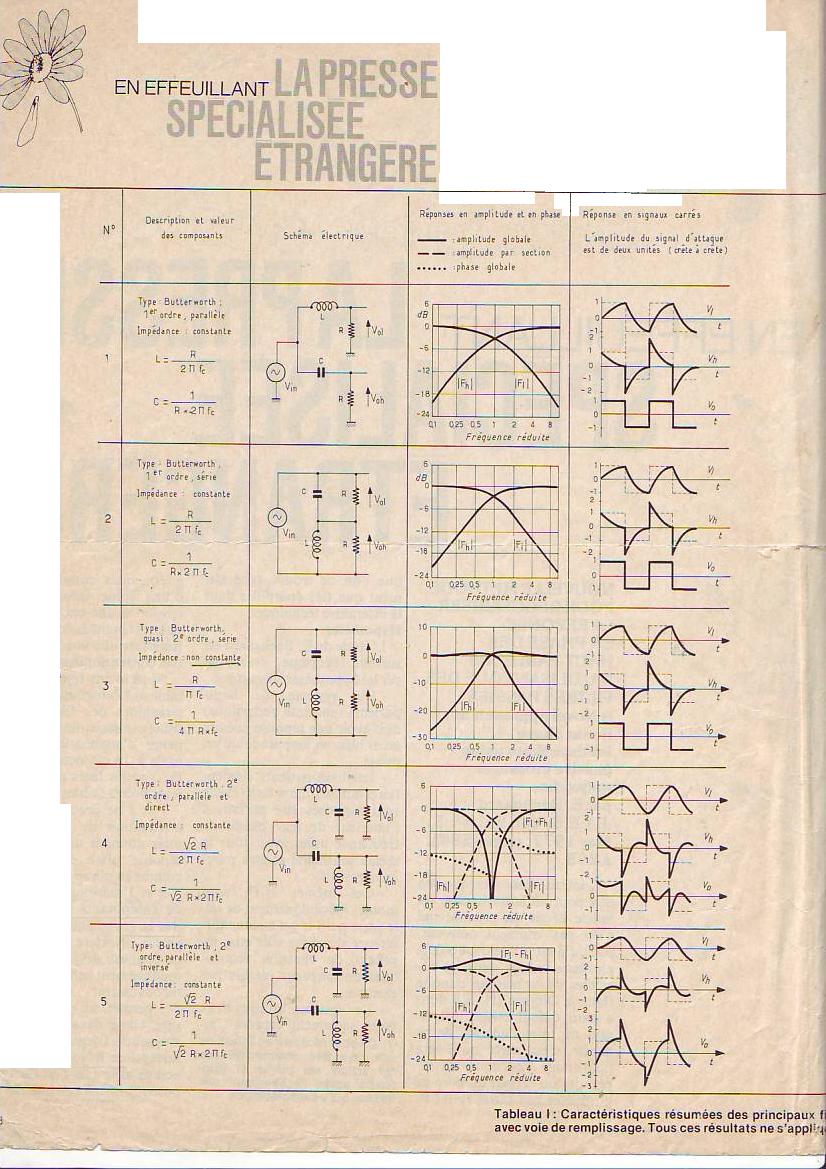
Page 3/4 :

Les formules des filtres à 18 dB avaient un problème. Utilisez celles du site.

 

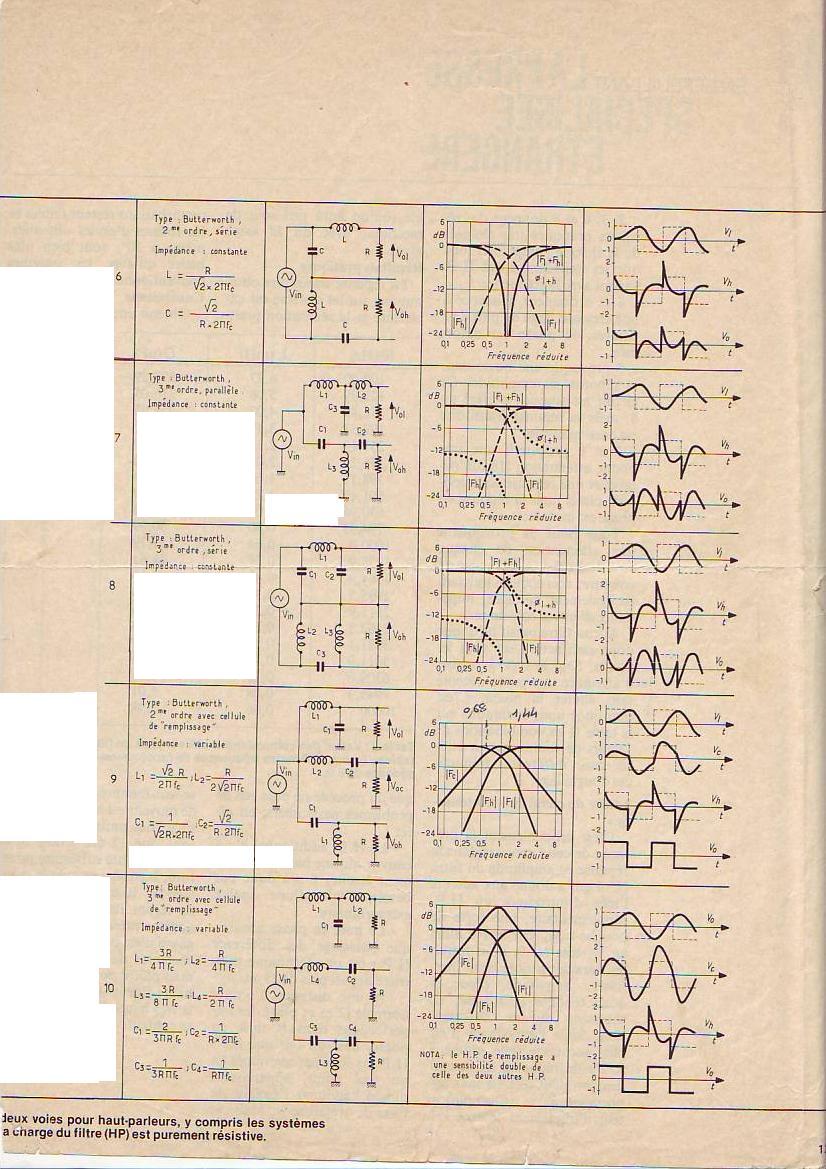
Page 4/4 :

 

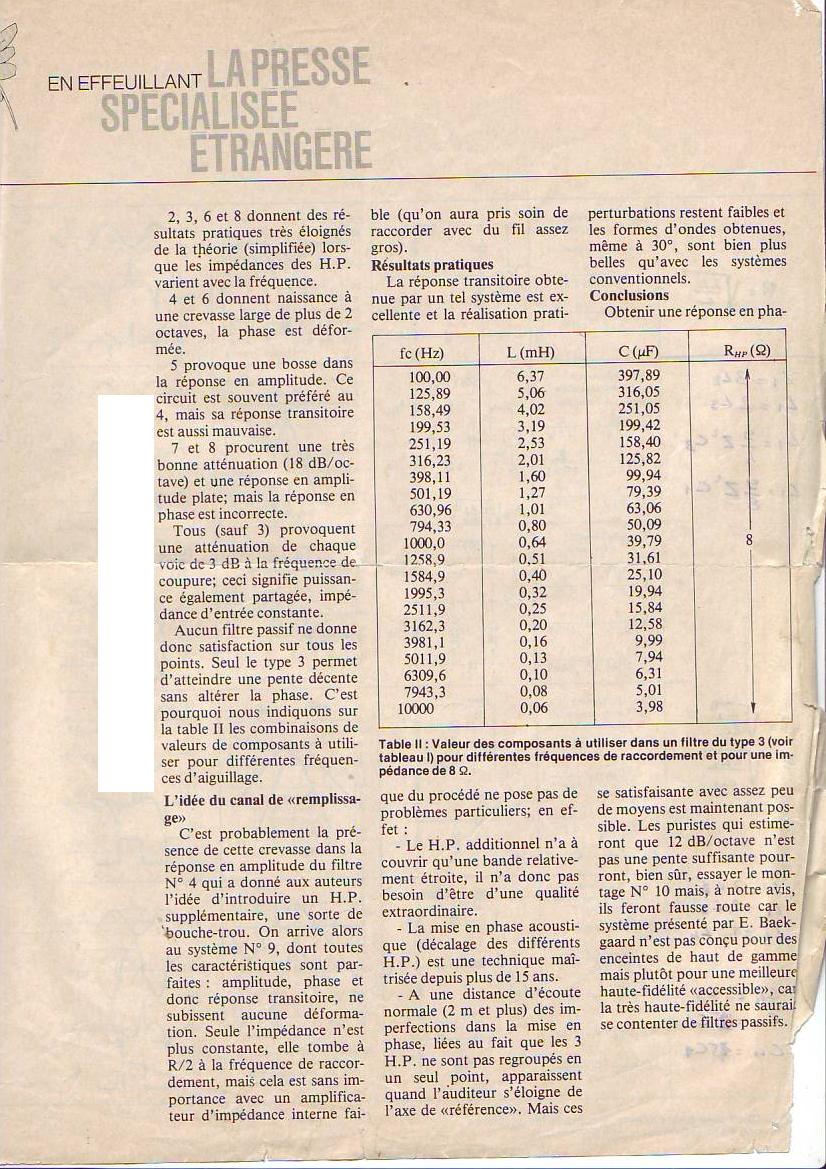
Un exemple de filtre en série à 3 voies à 6 dB/octave.

Avec les atténuateurs à impédance constante sur le médium et le tweeter.
Schéma du filtre trouvé sur un forum.
La fréquence centrale de calcul du filtre du médium, avec les équations du livre de Vance Dickason, est racine(5000 * 400 ) = 1414 Hz.

 

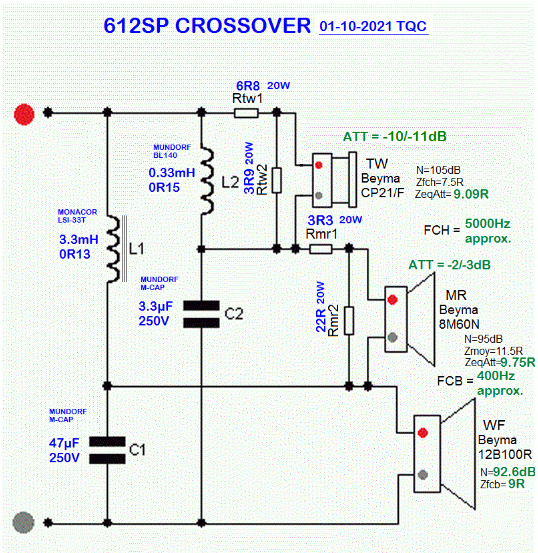
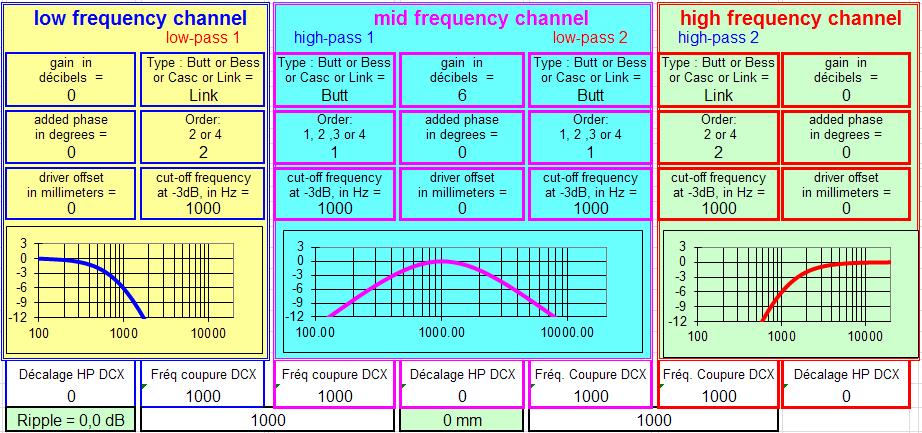
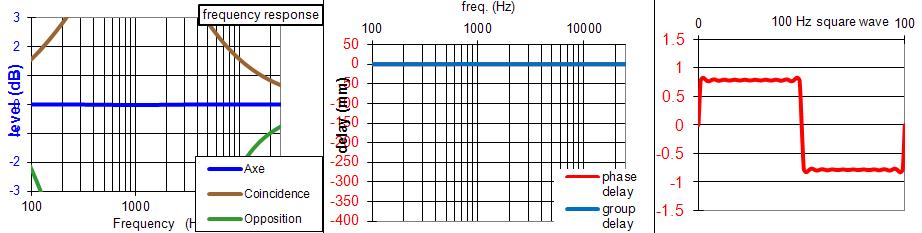
Haut-parleur relais à 12 dB/octave calculé avec les outils d'aujourd'hui, le tableur JMLC.

Courbe de réponse dans l'axe, délai, réponse sur signal carré sont rigoureusement conformes aux attentes.
Le troisième haut-parleur permet de ne pas inverser la phase du tweeter par rapport à celle du grave, tout est branché en phase sans le moindre délai.

J'ai du prendre un filtre Linkwitz Riley avec raccordement à -6 dB pour y arriver, la réponse en coïncidence n'est pas bonne, j'ai du ajouter 6 dB de gain sur le haut-parleur relais pour avoir une courbe qui tangente le 0 dB.

 

Télécharger le tableur JMLC (JMLC pour Jean Michel Le Cleac'h).
Les simulations ci-dessus sont obtenues avec une version modifiée de ce tableur, pour correspondre exactement au filtre actif DCX 2496.
Ces modifications ne concernent que l'ergonomie et la présentation, la base du calcul est à 100% celle du tableur JMLC, sans modification.
Les modifications apportées au tableur en téléchargement sont décrites dans le détail au bas du chapitre filtres 2 et 3 voies et tableurs JMLC.

Lorsque l'on compare d'un côté le filtre Butterworth à 12 dB/octave proposés par "La Revue du Son", de l'autre le filtre Linkwitz Riley à 12 dB/octave trouvés à la simulation, il est légitime de se poser la question de savoir lequel est juste, lequel est faux.
JMB apporte la réponse suivante :

Le problème en actif est très différent comparé au passif où se produit un effet de surtension avec L et C série sur le médium en bande étroite, d'où des formules différentes.
Il n'y a pas de transposition possible actif / passif.
Les deux solutions "parfaites" du Baekgaard diffèrent.
Les feuilles JMLC simulent de l'actif, il faut donc un Linkwitz Riley en actif, mais un Butterworth en passif.

La solution marche aussi parfaitement avec un petit écart entre les fréquences de coupure.
J'ai utilisé un certain temps la solution ci-dessous :

 

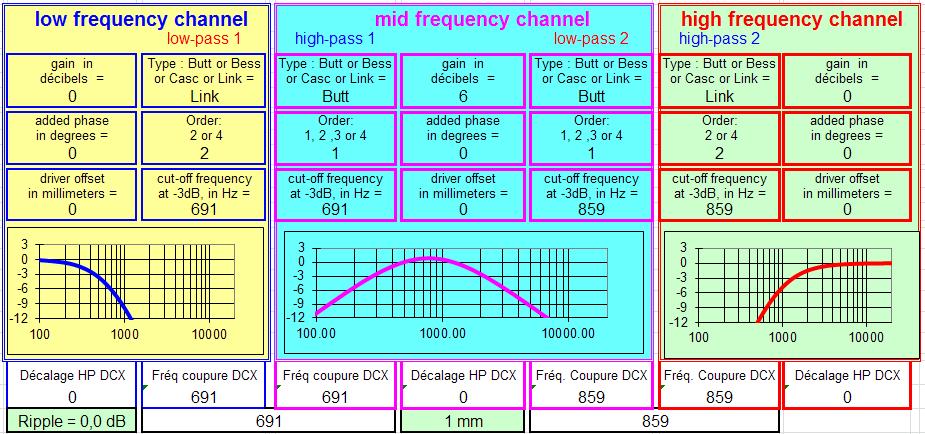
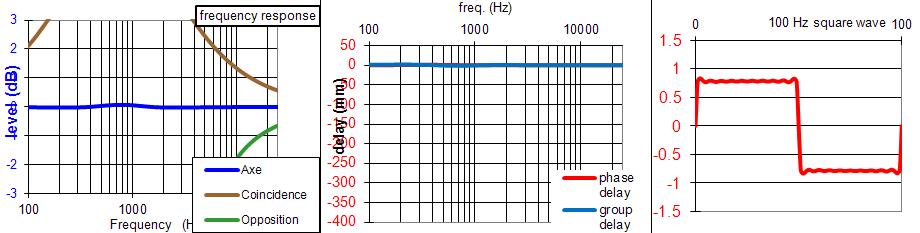
Il existe une autre solution de ce filtre, calculée par JMB, avec des coupures à 500 et 2000 Hz au lieu de 1000 Hz pour notre exemple, et avec une performance pratiquement égale à celle du filtre avec des fréquences de coupure identiques.
0.3 dB d'ondulation dans la courbe de réponse, pour 2 octaves entre la coupure du grave et celle du tweeter, c'est particulièrement intéressant.

 

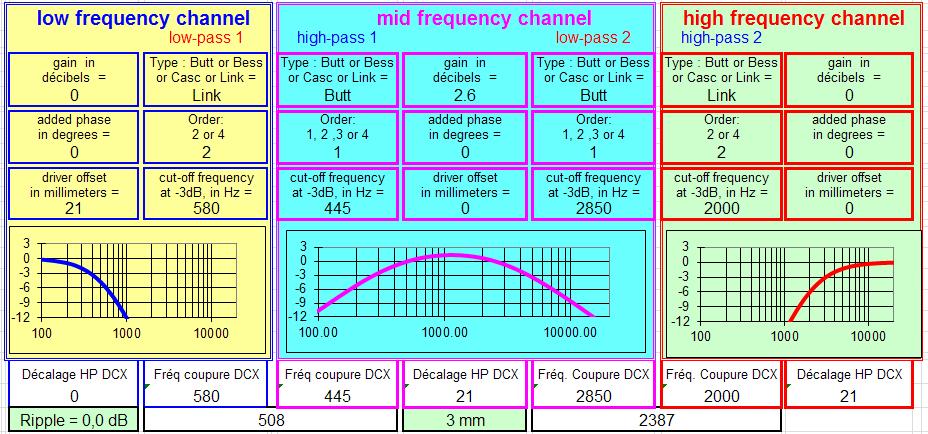
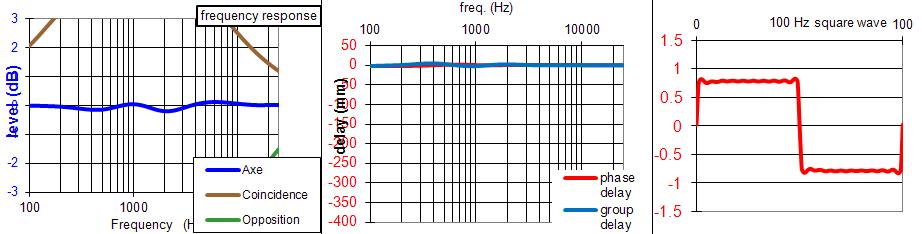
Explications par JMLC sur la réponse dans l'axe et en coïncidence :
Image du lien ci-dessus de la partie que je souhaite expliquer.

 

haut-parleur relais à 18 dB/octave :

Solution en filtrage passif :

Cette solution est réalisable facilement avec un filtre passif, en utilisant les formules du schéma ci-dessous qui correspondent exactement au schéma numéro 10 de "La Revue du Son", sans erreur.

 

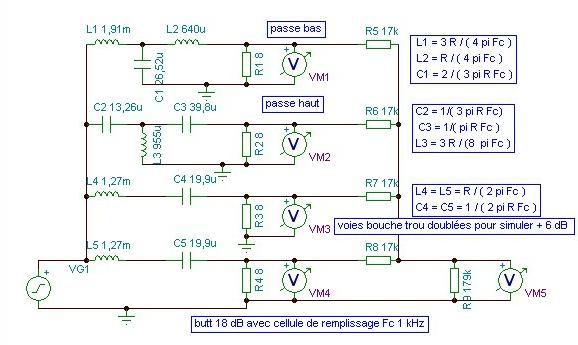
Solution en filtrage actif :

Cette deuxième solution ci-dessous est une variante, expliquée par JMB :

C'est un Baekgaard "élargi" ou les voies hautes et basses, en 18 dB, résultent de la mise en série de deux fonctions LR 12 + Butt1 à 1 kHz... (d'où le -9 dB au raccord) et bande au médium plus large.

• Avec un filtre actif tel que le DCX qui ne dispose que du filtre Butterworth à 18 dB/octave, il faut mesurer les haut-parleurs filtrés, et égaliser dans la pente pour obtenir la courbe d'atténuation voulue, avec - 9 dB à la fréquence de coupure.
  Avec cette méthode, vous êtes dans l'utopie la plus totale, je défie quiconque d'y arriver. (J'ai essayé...)
• Cela peut être obtenu avec le filtre à 12 dB de type Linkwitz Riley dans le DCX, et un filtre à 6 dB entre le filtre actif et l'ampli, tel celui décrit au chapitre " Filtre actif passif KANEDA".
  Cette méthode a toutes les chances de fonctionner, mais je ne l'ai pas essayée.

Suite à la mise au point de mon système avec un haut-parleur relais à 12 dB/octave, je considère qu'il est tout à fait illusoire de vouloir essayer de linéariser un haut-parleur "dans la pente" en suivant une courbe d'atténuation.
Vous linéarisez le haut-parleur non filtré dans un premiers temps, vous le filtrez dans un 2^e temps.

 

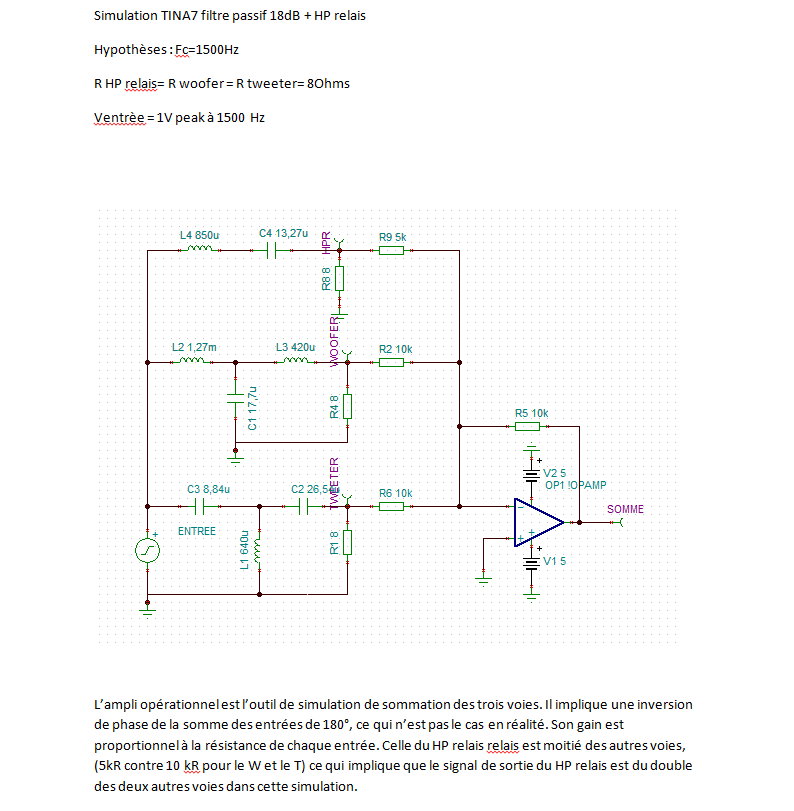
Simulation du filtre par Georges :

Je tiens à préciser, au cas où cela soit nécessaire, que le signal du "haut-parleur relais" doit être du double de celui qui est représenté sur le diagramme que je vous ai envoyé , pour avoir une réponse globale plate.
En effet, pour cette simulation et pour des raisons pratiques, les signaux des trois haut-parleurs sont prélevés avant les résistances sommatrices de l'ampli op.
Celle du haut-parleur R est deux fois plus faible que les deux autres, son signal compte pour double dans le signal dont on fait la somme.

 

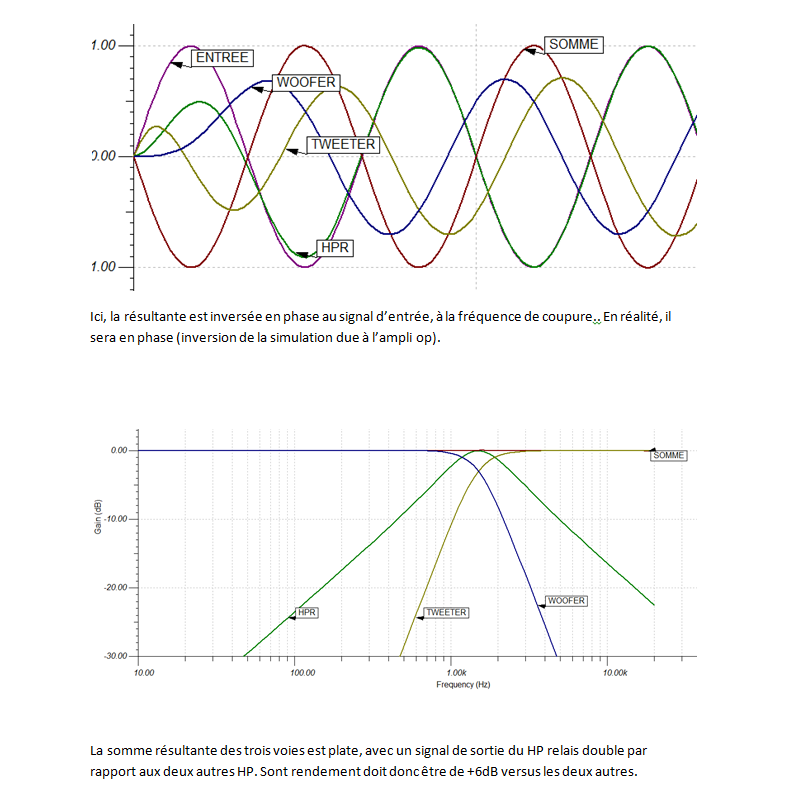
La courbe ci-dessous est une courbe théorique qui correspond à la solution filtre actif décrite ci-dessus, 12 dB/octave Linkwitz Riley + 6 dB/octave Butterworth.
Le but est d'avoir des courbes aussi précises que possible, pour pouvoir relever les valeurs directement sur les courbes, et comparer avec la mesure.

Filtre de coupure du filtre actif à 18 dB/octave avec un haut-parleur relais : 640.0 Hz.

Fréquence de coupure du filtre en Hz :

 

 

Dôme Acoustique