Page affichée à 17:21:23
dimanche 01 octobre 2023
Ce site n'utilise pas de cookie.Dôme acoustique Compteur pour tout le site : 13 036 875
Nombre actuel de lecteurs : 17.Le site de Dominique, un amateur passionné
2-6-2-1 : Filtres 2 et 3 voies et simulateur JMLC
Mise à jour : 30 juin 2012.
Solution habituelle :
Avant d'envisager n'importe quel filtre, je vous invite à utiliser le simulateur théorique de filtres JMLC (JMLC pour Jean Michel Le Cleac'h), et de vérifier le filtre que vous prévoyez.
Simulateur 4 voies avec réponse sur un signal carré.
- Si le résultat vous convient allez y.
- Si le résultat est catastrophique, réfléchissez bien à votre projet.
Les simulations ci-dessous sont obtenus avec un tableur, et seront progressivement modifiés si vous m'en faites la demande.
Quelques remarques pour réussir une enceinte correctement filtrée, et éviter les difficultées d'une enceinte à 3 voies :
- Un HP médium ne se justifie que si le grave dépasse 25 cm
- En choisissant bien vos HP, vous pouvez faire une deux voies, avec un HP de 21 cm et un tweeter, pour un résultat plus que satisfaisant.
- Il existe des HP coaxiaux de 21 à 38 cm avec une compression au centre.
Bref, tout sauf du trois voies ?
Simulez votre filtre, vous comprendrez...
Regardez de très prés les solutions avec un HP relais :
- Qui sont des presque deux voies dans le choix des HP grave et tweeter.
- Qui sont des larges bandes dans le choix du HP relais.
- Avec un résultat global très satisfaisant, si choisissez les deux HP principaux de façon à ce qu'ils acceptent un filtre à 12 dB/octave.
Calcul des filtres 3 voies passifs
Le calcul n'est valable dans le cas d'un filtre passif que s'il y a un rapport égal à 8 ou 10 entre les deux fréquences de coupures.
Au delà de 15, calculez 2 filtres 2 voies.
Une coupure grave médium à 400 Hz, et une coupure médium aigu à 4000 Hz est valable : 4000 / 400 = 10.
Une coupure grave médium à 400 Hz, et une coupure médium aigu à 3200 Hz est valable : 3200 / 400 = 8.
Une coupure grave médium à 800 Hz, et une coupure médium aigu à 2000 Hz n'est pas valable : 2000 / 800 = 2.5.Les critères ci-dessus ne s'appliquent pas au filtrage avec un HP relais, qui est une deux voies à la base.
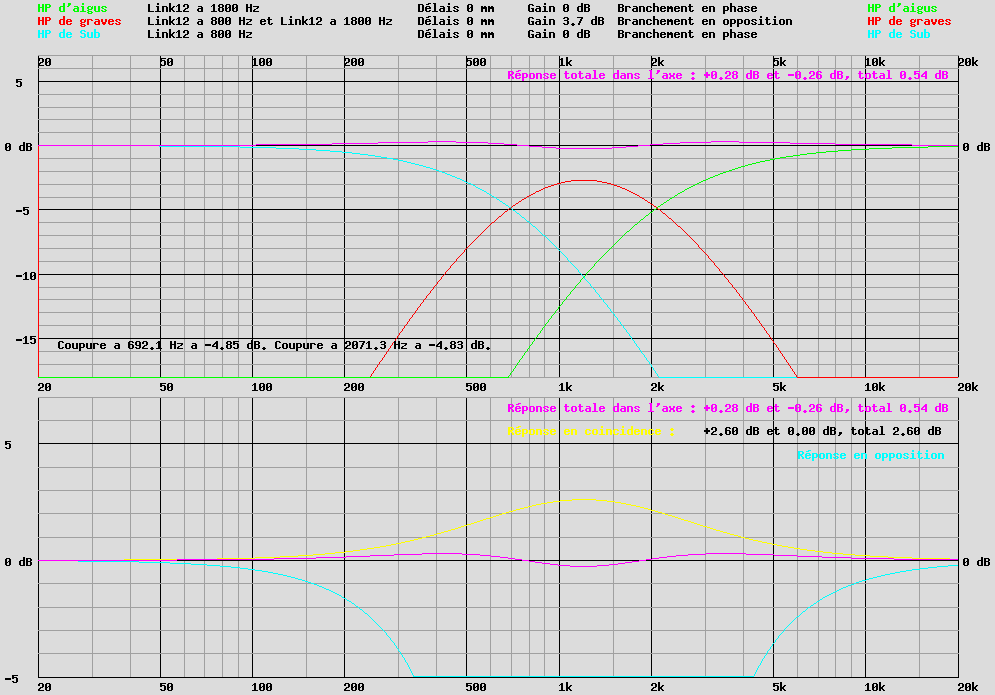
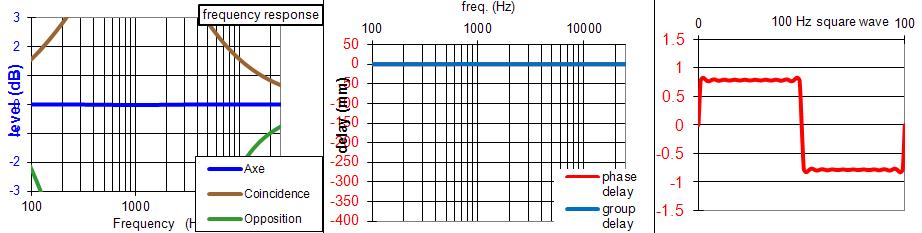
Avec un filtre actif, si la simulation avec les tableurs vous convient, vous pouvez la réaliser dans votre filtre actif qui n'a pas les limites de calcul des filtres passifs.L'exemple en image ci-dessous explique bien le problème des coupures trop proches entre grave, médium et aigu.
Vous vouliez des coupures à 800 et 1800 Hz à -6 dB en Linkwitz Riley à 12 dB/octave, vous obtenez des coupures à 692 et 2071 Hz à -4.8 dB avec un médium qui doit avoir une sensibilité de +3.7 dB que prévu.
La courbe en coincidence, qui devait être rigoureusement plate, est à +2.6 dB.
Enfin si la simulation indique le résultat avec un filtre actif, le calcul des composants passifs n'est pas possible a cause des interactions des filtres entre eux.
Ce point va entraîner des perturbations énormes par rapport au calcul théorique.
La conclusion est toute simple, Pas de filtre 3 voies en passif s'il n'y a pas au moins un rapport de 8 entre les fréquences de coupure.
Pourquoi une simulation de filtre ?
Il ne suffit pas que la réponse en fréquence soit parfaitement linéaire pour que les résultats soient bons.
Il faut aussi que les fréquences graves, médiums et aigus arrivent ensembles dans le temps.
Cela demande des délais entre les haut-parleurs, et aussi et surtout que le filtre n'ai pas de retard variable avec la fréquence.
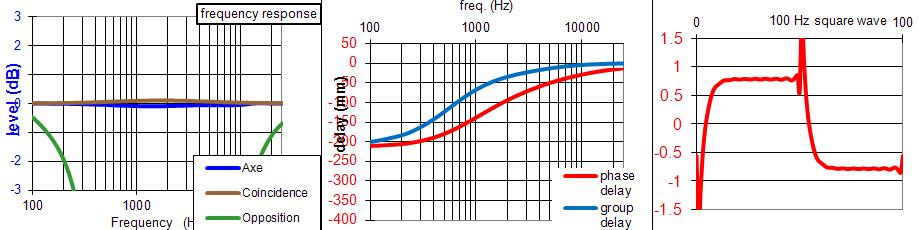
- La réponse en fréquence parfaitement linéaire se voit avec la courbe bleu de la réponse en fréquence, courbes de gauche.
Une réponse en coïncidence très proche de la courbe bleue est un avantage, recherché par certain.
- L'absence de retard variable avec la fréquence se voit sur les délais de phase et de groupe, sur les courbes du centre.
Plus les courbes restent proches de 0, mieux c'est.
Au dessus de 4000 Hz, la différence n'est plus audible, dixit les spécialistes.
- La réponse sur signal carré donne de précieuses informations. Courbe de droite.
Vous devez obtenir un carré, regardez le filtre à 6 dB ou celui avec un HP relais pour voir ce qu'est un beau signal carré...Vous pouvez trouver sur internet des simulations de filtre passif avec une courbe de réponse absolument parfaite.
Ces simulations oublient simplement de voir les choses dans le temps, et ne vous garantissent pas des délais de phase et de groupe correct, un signal carré qui ressemble à un signal carré.
De toute façon, si vous demandez au filtre passif de corriger la réponse accidentée de vos HP, vous ne serez bons que sur la courbe de réponse et pas sur les autres critères.
Les filtres actifs numériques ont un avantage incontestables sur ce point, avec une correction des HP avant filtrage, et un filtrage parfaitement conforme à la théorie.Il n'y a pas de solution de filtrage parfaite sur tout les critères.
C'est la solution avec HP relais qui m'a apporté les plus grandes satisfactions à l'écoute.
Considérez que c'est une deux voies, avec un 3eme HP "bouche trou".
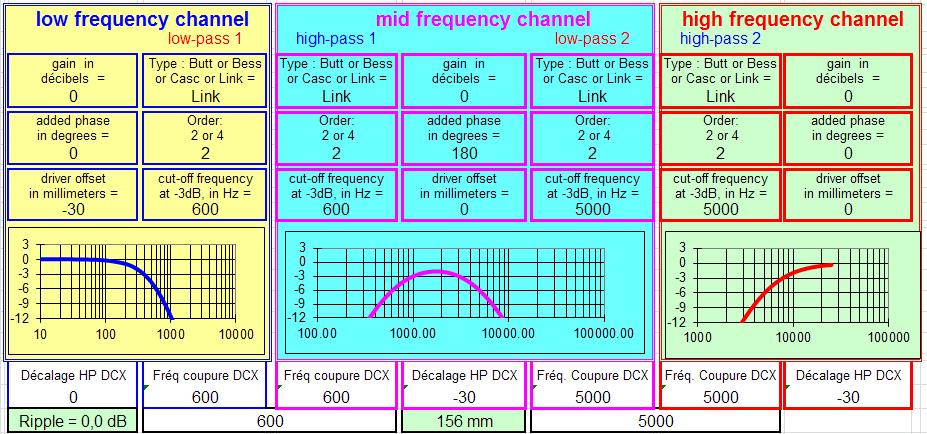
Filtre 3 voies à 12 dB/octave Linkwitz Riley :
Ce filtre convient très bien pour une coupure grave médium assez haute, tel les 600 Hz proposés, et une coupure médium aigu éloignée de la coupure grave médium, avec au moins un rapport de 8 ou 10 entre les deux.
Si vous voulez filtrer en passif à 500-5000 Hz, 600-6000 Hz, 600-5000 Hz par exemple, ce filtre est parfait.
Le retard, pas courant, du HP de grave vous évite d'avoir a reculer le HP de médium par rapport au grave.
L'influence du retard est faible, si vous avez en pratique 20 mm au lieu des 30 mm, c'est pratiquement sans importance.
Filtre 3 voies à 18 dB/octave Butterworth :
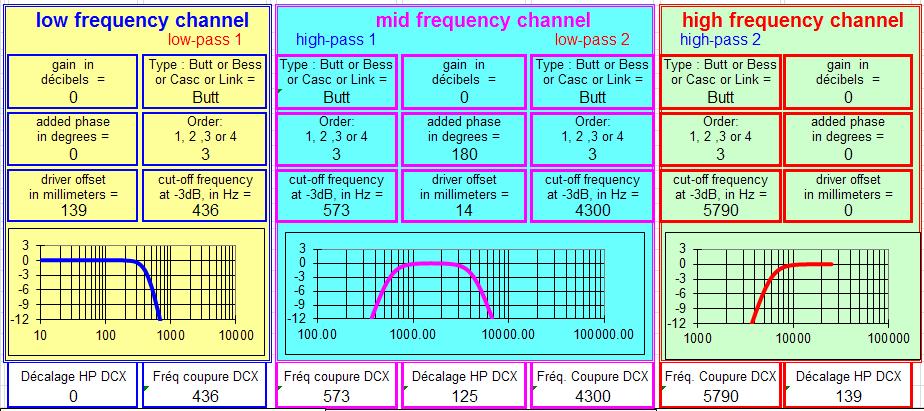
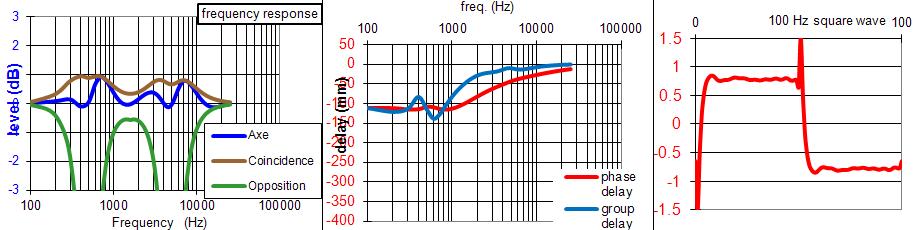
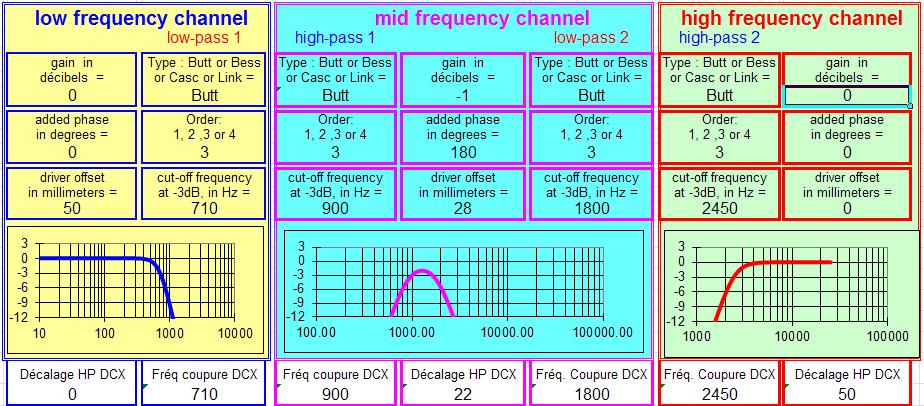
Avec des fréquence de coupure proche de 800 et 2100 Hz :
Cette solution est réalisable avec un filtre actif.
Elle n'est pas alculable avec les outils de ce site qui demandent un rapport de 10 entre les fréquences de coupure.
Il existe d'autres formules pour un rapport de 8, voir le livre de Vance Dickason : Enceintes acoustiques & haut-parleurs.Une trois voies n'est pas l'addition de deux fois deux voies, c'est clair surtout si les Fc sont proches, cependant, avec un peu d'inspiration, il est possible de trouver la solution tenant compte de l'interaction des pentes de manière à se rapprocher du modèle quasi-optimal visé.
Il importe de retrouver un retard de phase le + constant possible idem les courbes mais "ça marche".
Dada.
Filtres 3 voies à 12 dB/octave, avec HP relais :
C'est une solution proposée par La Revue du SON en 1977 : Le filtrage avec un HP relais.
Attention :
La simulation est valable pour un filtre actif.
En passif il faut utiliser un filtre Butterworth à 12 dB/octave, avec les formules du lien ci-dessus.
Il existe une solution à 18 dB/octave, réalisable uniquement avec un filtre passif, voir le lien ci-dessus.Courbe de réponse dans l'axe, délai, réponse sur signal carré sont la référence.
Le troisième HP permet de ne pas inverser la phase du tweeter par rapport à celle du grave, tout est branché en phase sans le moindre délai.
La réponse en coïncidence est une catastrophe, j'ai du ajouter 6 dB de gain sur le HP de remplissage.Comparez ce filtre avec le filtre 2 voies à 6 dB/octave, et regardez les pentes de ce filtre sur le grave médium et le tweeter...
Comment le réaliser en pratique ?
Un grave médium, un tweeter capable d'être coupé bas, et deux larges bandes en pseudo MTM de part et d'autre du tweeter par exemple.
La bande passante des larges bandes est très grande, 100 à 10000 Hz à -15 dB pour une coupure à 1000 Hz, tenez en compte.
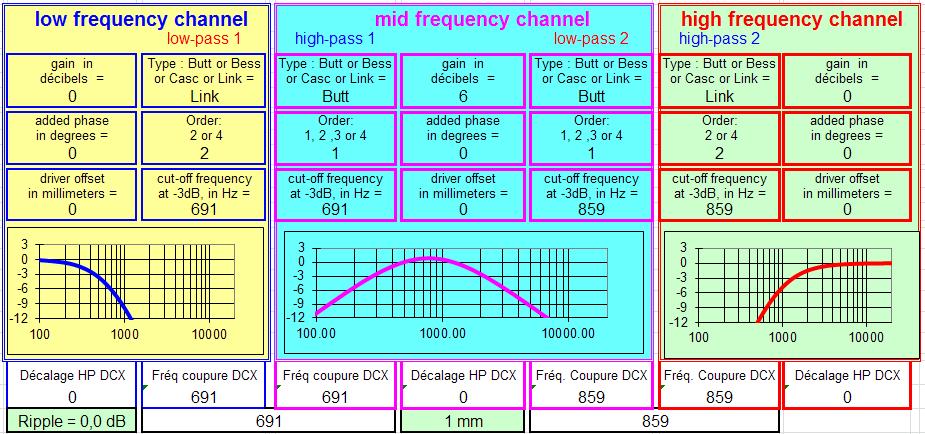
La solution marche aussi parfaitement avec un petit écart entre les fréquences de coupure.
J'utilise la solution ci-dessous :
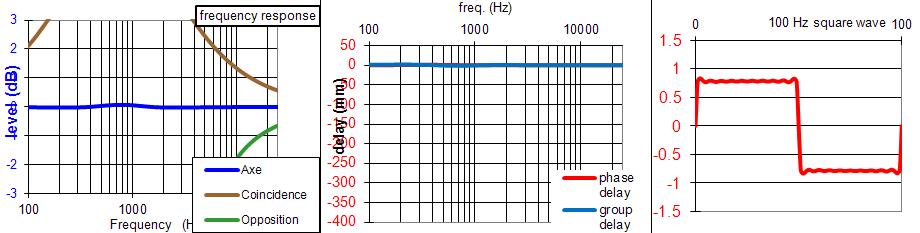
JCB m'a envoyé cette autre solution avec une bande passante plus large, un résultat pratiquement aussi bon, et un HP relais qui a besoin d'une sensibilité pas trop élevée, +2.7 dB au lieu de +6 dB.
Nous sommes en filtrage actif, la différence de sensibilité n'est pas importante.
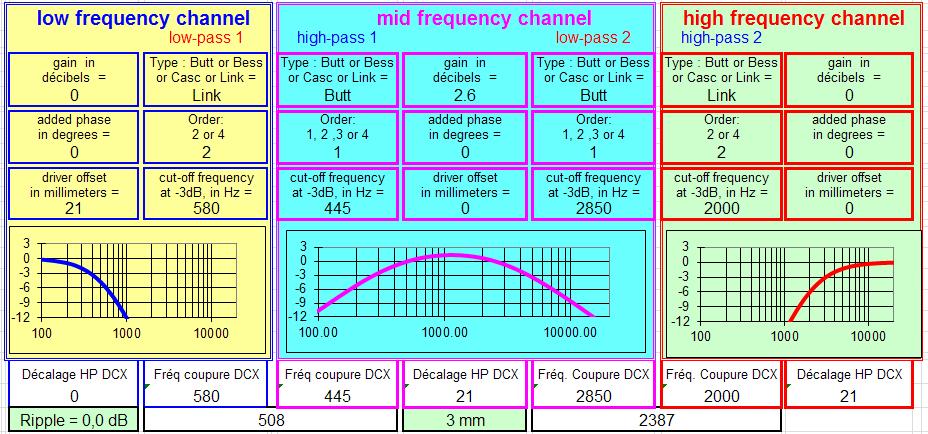
Filtres 3 voies à 24 dB/octave, avec HP relais :
Avec un HP proche du HP relais, mais avec un écart plus grand au niveau des fréquences de coupure.
Cette solution a été proposée par Dada sur le forum AUDAX.
Les images de la simulation n'étaient pas dans le forum, je les ai simulées et ajoutées.Plusieurs mois après, j'ai reçu un email deJMB me proposant une version retravaillée de la solution, avec une image pour préciser exactement les valeurs à utiliser.
C'est cette 2eme version, avec une courbe de réponse pratiquement parfaite, qui est proposée ici.Je continue à jouer avec la feuille de JLMC, et voici une mouture en 3 voies, ou plus précisément en 2 voies + " bouche trou " qui me semble présenter un intérêt.
Pour ceux qui ont envie de simuler ce filtre, je vous donne tout de suite ses caractéristiques, on verra le potentiel plus tard.Les voies grave et aigu sont distantes de 2 octaves ( Fc -3 dBs ) et pour combler le trou central ( -13 dBs au milieu sur le PB et le PH ), une voie médium en " bouche-trou ", peu sollicitée ( son niveau maxi se situe 5 dBs en dessous du grave et de l'aigu ), filtrée en passe-bande.
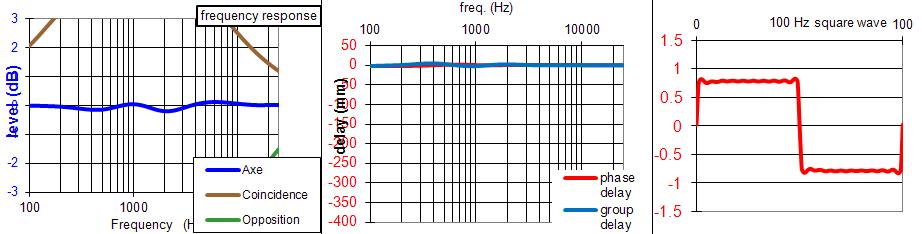
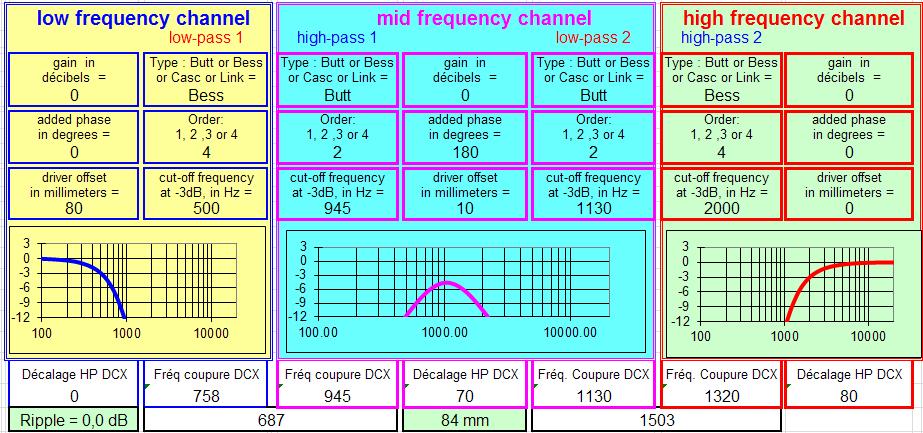
La courbe en coïncidence est parfaite, la courbe dans l'axe ne présente qu'un trou de 0,5 dB entre Fc et 2.Fc, et le délai de groupe, assez élevé dans l'absolu, est parfaitement linéaire jusqu'à la fréquence centrale du bouche trou, la liaison a l'air assez " transparente " au moins dans cette jonction sensible entre le grave et le médium ...Pour l'exemple donc, avec la classique Fc = 1000 Hz ( et C = 343.707 m/s = 343707 mm/s ) :
- PB du grave en Bessel 4 à Fc / 2. 500 Hz ici.
- PH de l'aigu en Bessel 4 à Fc * 2. 2000 Hz ici.
- PH du médium en Butterworth 2 à Fc * 0.945. 945 Hz ici.
- PB du médium en Butterworth 2 à Fc * 1.130. 1130 Hz ici.
- Recul du médium : 0.2037 * longueur d'onde à Fc. 0.2037 * 343707 / 1000 = 70 mm.
- Recul du tweeter : 0.2328 * longueur d'onde à Fc. 0.2328 * 343707 / 1000 = 80 mm.
Les décalages positifs sur la feuille de JMLC correspondent à une avance du HP.
Dans l'exemple ci-dessous, c'est avance du boomer = 80 mm et avance du médium = 10 mm.
Traduit en programmation des délais sur un DCX ou autre BSS, il faut rentrer : Recul du tweeter 80 mm et recul du médium = 70 mm.
Pour en discuter ... dada ...
Pour le cas ci-dessus :
- Le BESS 4 à 500 Hz du grave devient 500 * 1.515 = 758 Hz dans le DCX.
- Le BESS 4 à 2000 Hz du tweeter devient 2000 * 0.660 = 1320 Hz dans le DCX.
Les tableurs JMLC sont une aide très précieuse et indispensable dans la mise au point des filtres.
Mais les délais d'un coté, le filtre BESSEL de l'autre, sont source de pièges difficilement admissible.
Je prends le problème en compte pour faire évoluer les choses.
Filtre 2 voies et demi :
C'est la solution que j'ai utilisé un certain temps sur mes baffles plans.
J'ai un grave de 38 cm, deux large bande de 21 cm et un médium tweeter de 12 cm.
Dans le grave, le 38 cm et les larges bandes travaillent ensembles.
Le grave est coupé à 92 Hz en pente douce à 6 dB/octave, les larges bandes continuent dans le médium jusqu'a la coupure avec le médium tweeter.Vous allez me dire que le grave est à +6 dB.
Je réponds que sur un baffle plan c'est un sacré avantage...
Au dessus de 200 Hz, le décalage est très limité et ceci jusqu'à 20000 Hz. L'écoute est bonne !!!
Enfin le décalage du signal carré vient du grave.Je ne dis pas que c'est une bonne solution, c'est simplement la solution que j'ai utilisé chez moi, jusqu'a trouver mieux...
Sachez que j'ai simulé et écouté un sacré bout de temps avant de prendre cette solution.
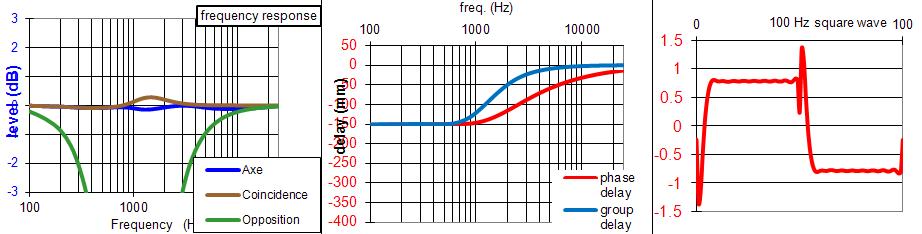
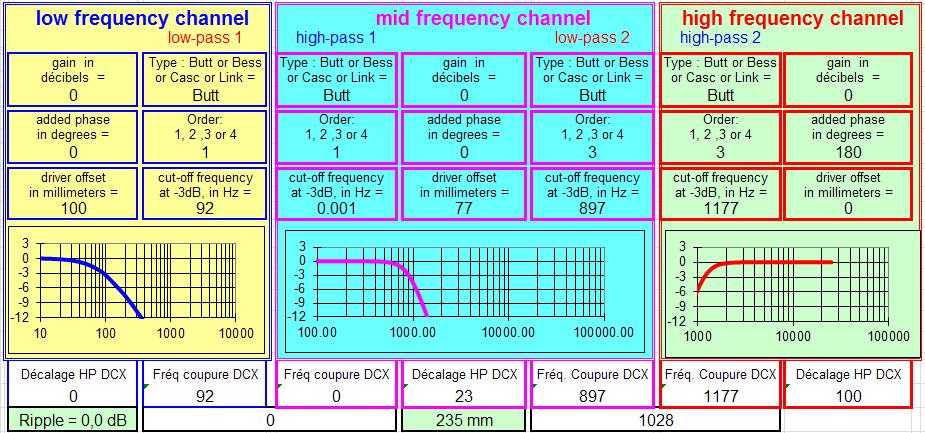
La solution présentée ci-dessous a été retravaillées par JMB.
Les valeurs réelles utilisées dans le DCX après mesures et écoutes sont de 0, 40 et 132 mm, au lieu de 0, 23 et 100 mm théorique, avec les phase telle que simulée sur le tableur.
Les différences de 17 mm entre grave et médium et de 15 mm sur le tweeter viennent des conditions géométrique du montage des HP.Sur ces feuilles il faut aussi se méfier de la manière dont la phase est prise en compte : Le résultat peut être absurde avec Fc basses.
JMLC écrit : " Un dépliement correct ( de la phase ) ne pourra intervenir qu'à partir de 258 Hz ".Je ne suis pas certain du tout de respecter cette prescription dans les deux images ci-dessous.
A vérifier en pratique avec les spécialistes, j'ai une version modifiée du tableur, version qui descend réellement à 10 Hz, avec un échelonnement irréprochable des fréquences de 10 à 100 Hz, et un soucis dans les délais à reporter dans le DCX lorsque le délai du médium est supérieur à celui du grave.
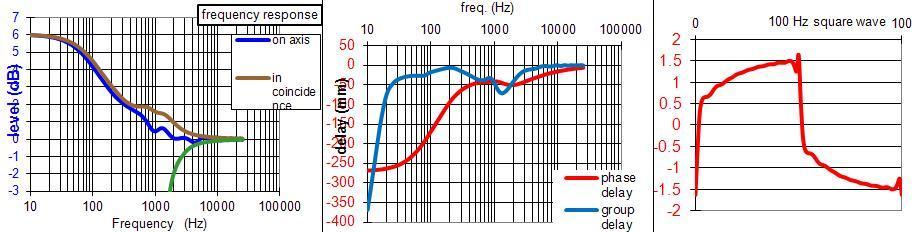
Filtres 3 voies à 12, 18 et 24 dB/octave :
JMB me suggère d'essayer la solution suivante, avec un HP bouche trou sur une bande passante plus étendue.
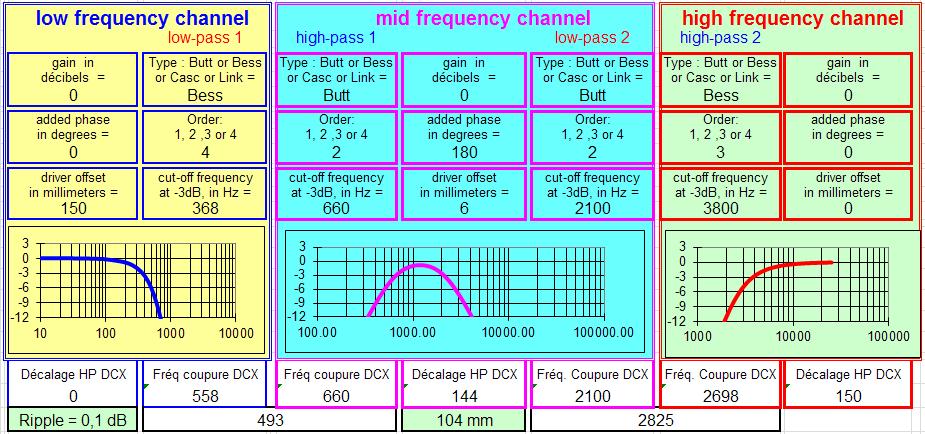
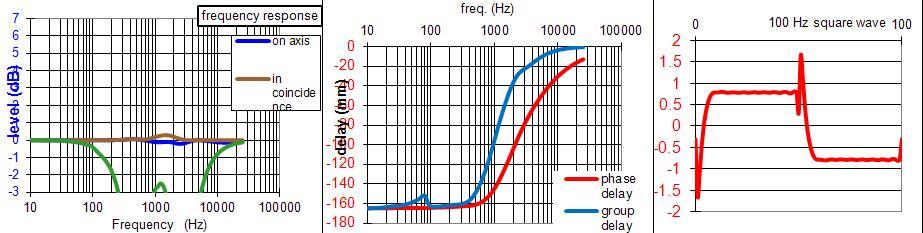
Sur la base de la proposition ci-dessus, nous avons échangé sur le cahier des charges, une coupure médium aigu centrée sur 1040 Hz avec des pentes du 3e ou 4e ordre, pour être compatible avec le montage MTM.
JMB a calculé deux propositions :
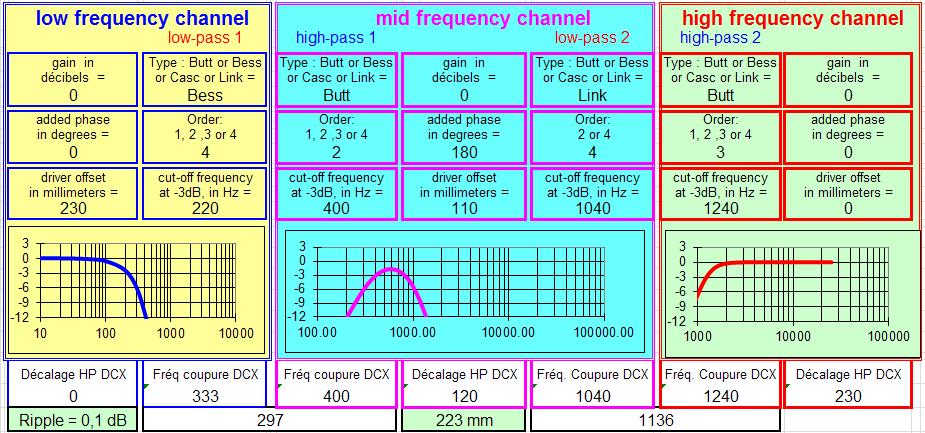
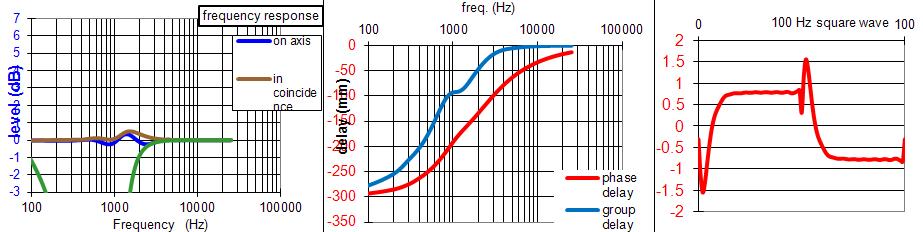
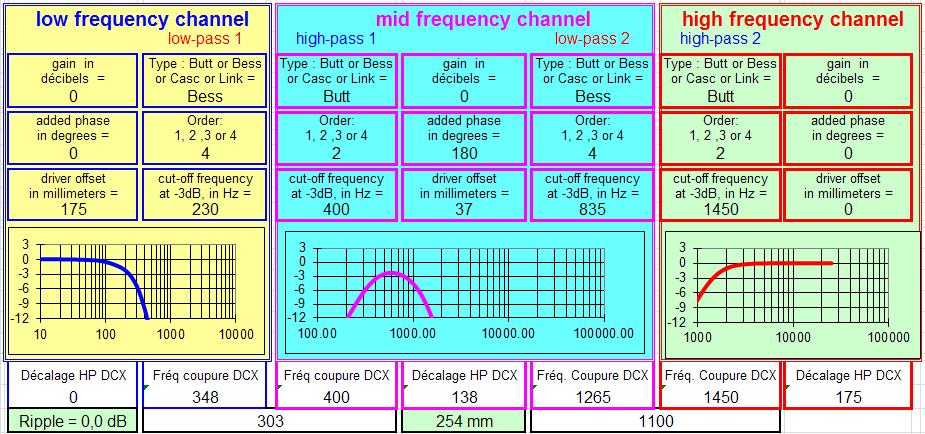
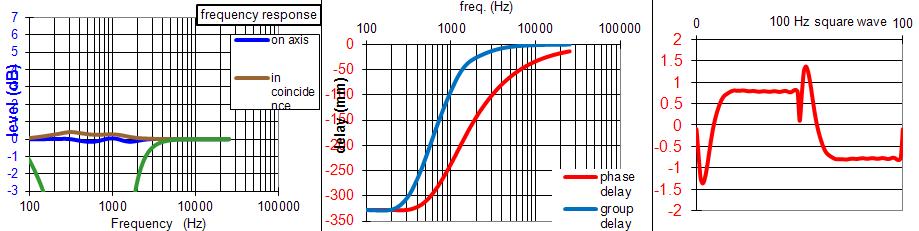
Enfin cette dernière solution est parfaitement applicable aux baffles plans à 3 voies, avec un grave, un médium et un tweeter conventionnel, avec le souhait de couper plus haut en fréquence le tweeter, et l'autre souhait de faire monter un peu plus le grave.
La simulation est toujours de JMB.
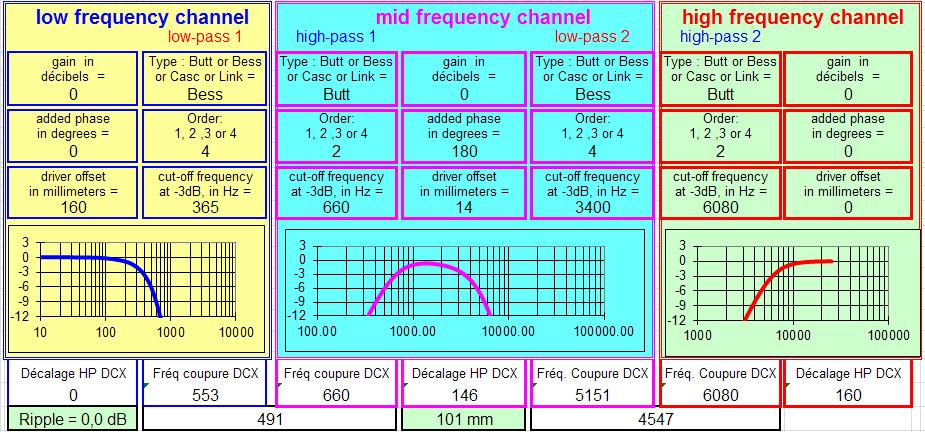
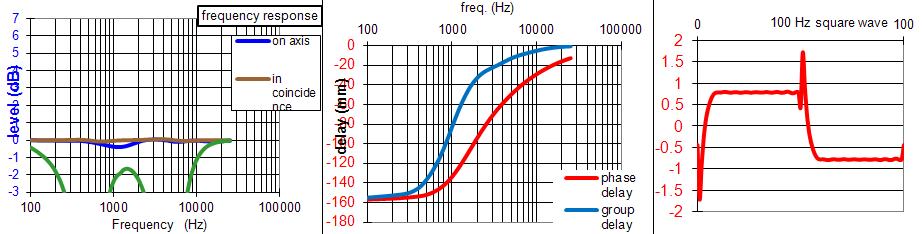
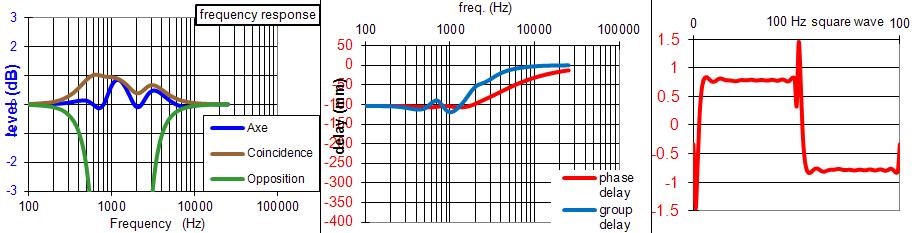
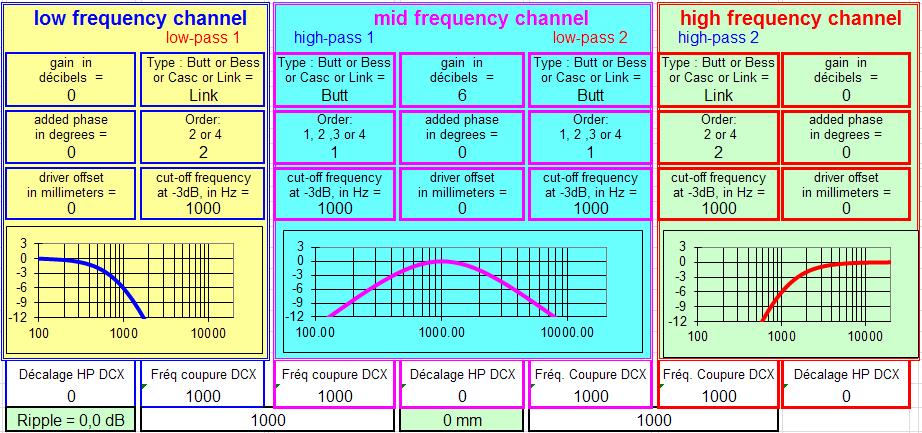
Le filtre à 2 voies à 6 dB/octave.
Filtre à 6 dB :
Pour beaucoup c'est le meilleurs filtre possible.
C'est vrai sur certain point, le signal carré est parfait, les délais de phase et de groupe sont à 0, la réponse dans l'axe est parfaitement plate.
Mais la réponse en coïncidence passe par +3 dB à la fréquence de raccordement : Il n'est pas possible de tout avoir à la fois...Pour réellement avoir les propriétés du filtre à 6 dB, la bande passante avant filtrage devrait être plate jusque 3 octave avant ou après la fréquence de coupure à -3 dB.
Vous voulez filtrer votre grave-médium à 1000 Hz ? La bande passande avant filtrage devrait rester plate jusque 8000 Hz.
Vous voulez filtrer votre compression à 1000 Hz ? La bande passante avant filtrage devrait rester plate jusque 125 Hz.
Personne ne respecte cette règle, donc personne n'a les réelles propriétés du filtre à 6 dB qui n'est qu'une utopie.
L'utopie du filtre à 6 dB/octave.
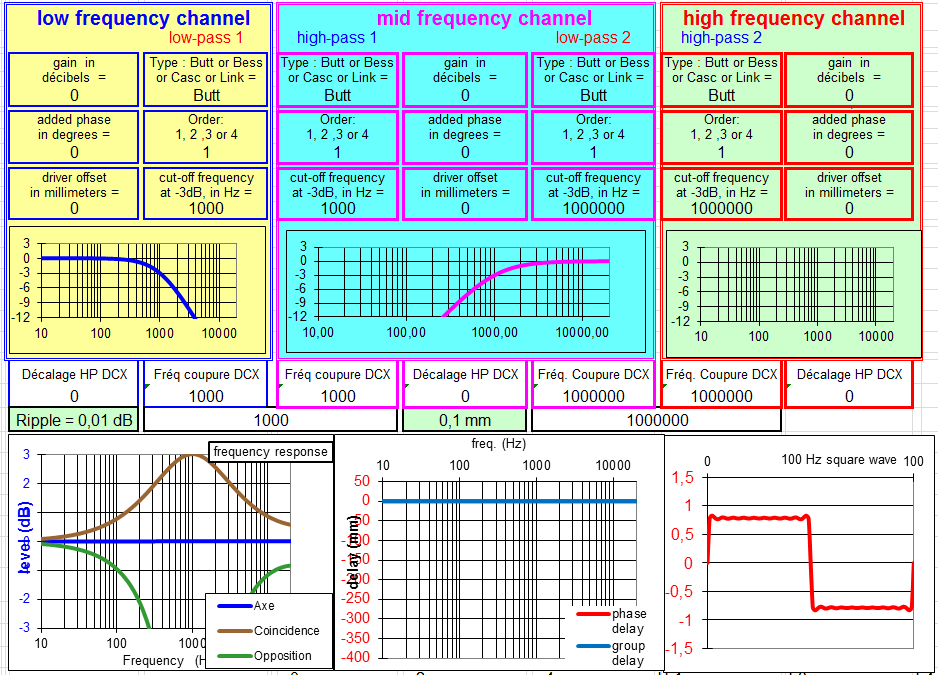
Les filtres à 2 voies à 12 dB/octave.
Filtre à 12 dB/octave Linkwitz Riley :
La réponse dans l'axe et en coïncidence sont pratiquement plate, les délais de phase et de groupe n'ont pas d'accidents, le signal carré est bon, pas de décalage des HP, un bon filtre facile à utiliser.
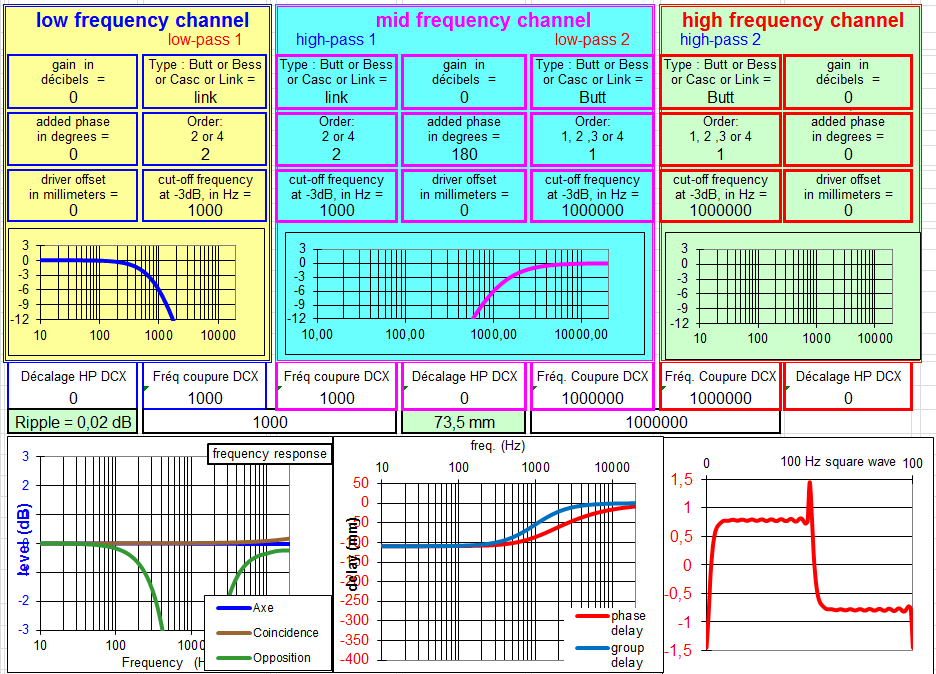
Filtre à 12 dB/octave Bessel :
La réponse dans l'axe et en coïncidence sont pratiquement plate, les délais de phase et de groupe n'ont pas d'accidents, le signal carré est bon, pas de décalage des HP, un bon filtre facile à utiliser.
Si vous lisez le livre de Vance Dickason : Enceintes acoustiques & haut-parleurs, les fréquences de coupure dans le DCX devraient être à 900 et 1100 Hz.
Le coefficient de correction est de 1.1 :
1000 * 1.1 = 1100 Hz et 1000 / 1.1 = 909 Hz.
J'ai trouvé des valeurs très légèrement différente sur les graphique avec un coefficient de correction de 1.13 :
1000 * 1.13 = 1130 Hz et 1000 / 1.13 = 885 Hz.
Je ne vois pas de différence significative avec le filtre Linkwitz Riley.
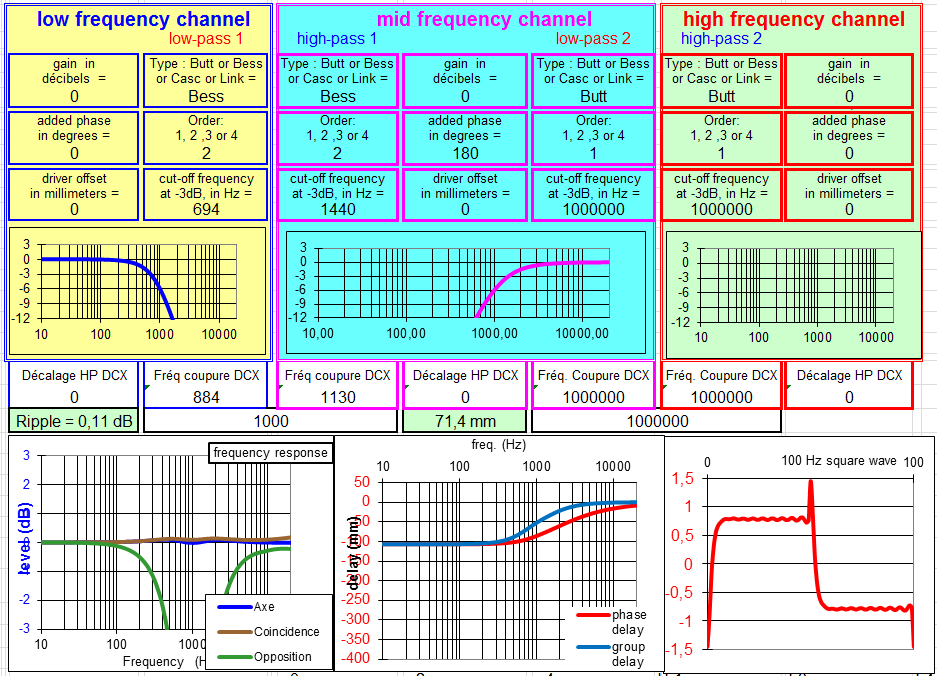
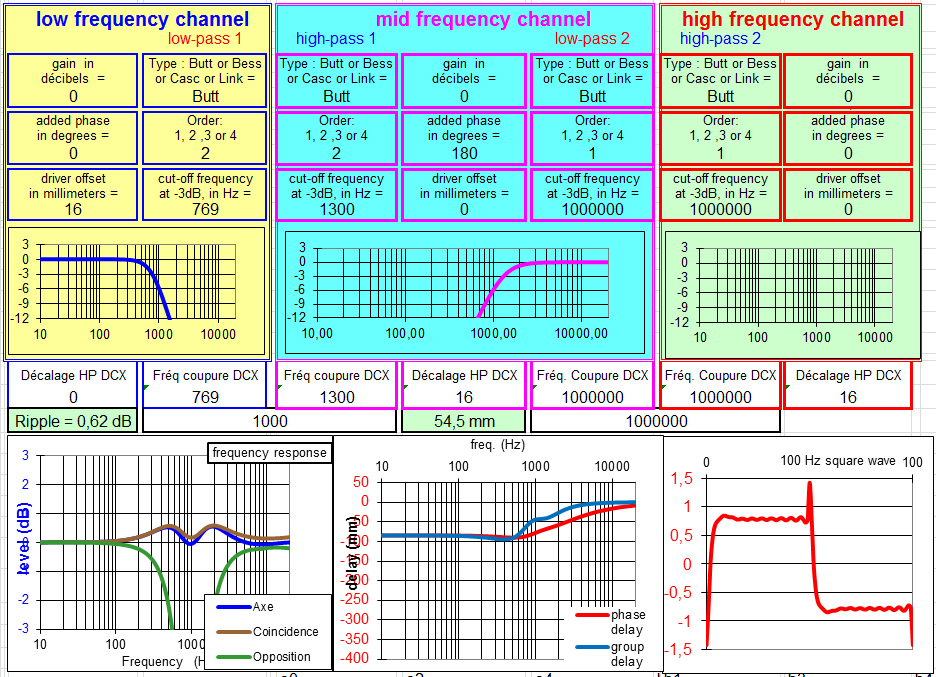
Filtre à 12 dB/octave Butterworth :
Si vous lisez le livre de Vance Dickason : Enceintes acoustiques & haut-parleurs, les fréquences de coupure pour avoir les meilleurs résultats sont à 769 et 1300 Hz.
Je n'ai pas réussi à faire mieux.
Le coefficient de correction est de 1.30 : 1000 * 1.30 = 1300 Hz et 1000 / 1.30 = 769 Hz.
Comparé au filtre Linkwitz Riley ou Bessel, les résultats sont moins bons.
A ne pas utiliser ?
Les filtres à 2 voies à 18 dB/octave.
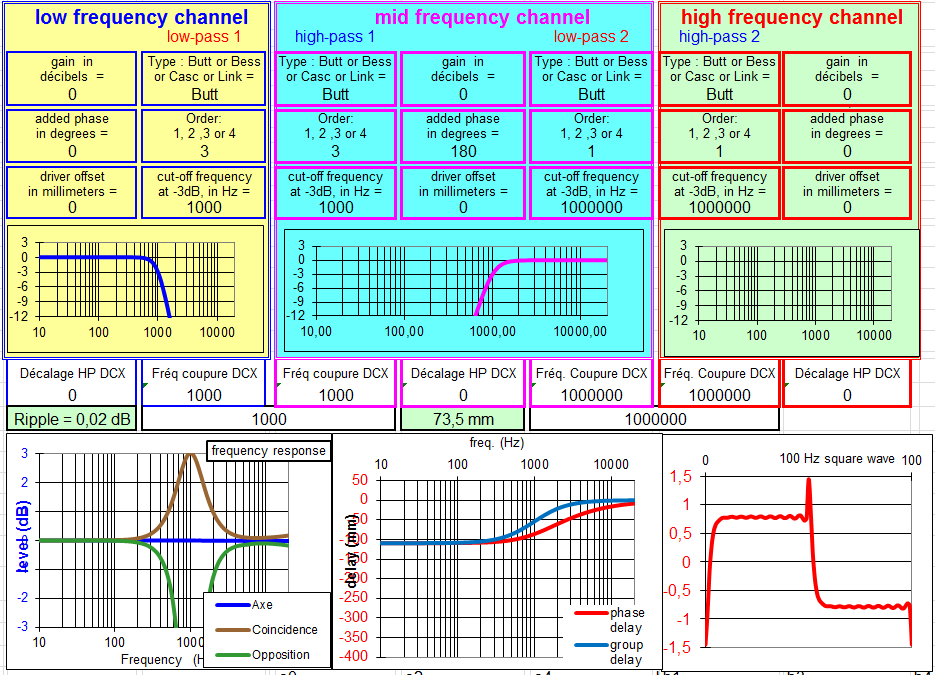
Filtre à 18 dB/octave avec raccord à -3 dB :
S'il n'y avait pas la courbe en coïncidence qui est à +3 dB à 1000 Hz, et au dessus de +1 dB de 500 à 2000 Hz, ce serait un très bon filtre.
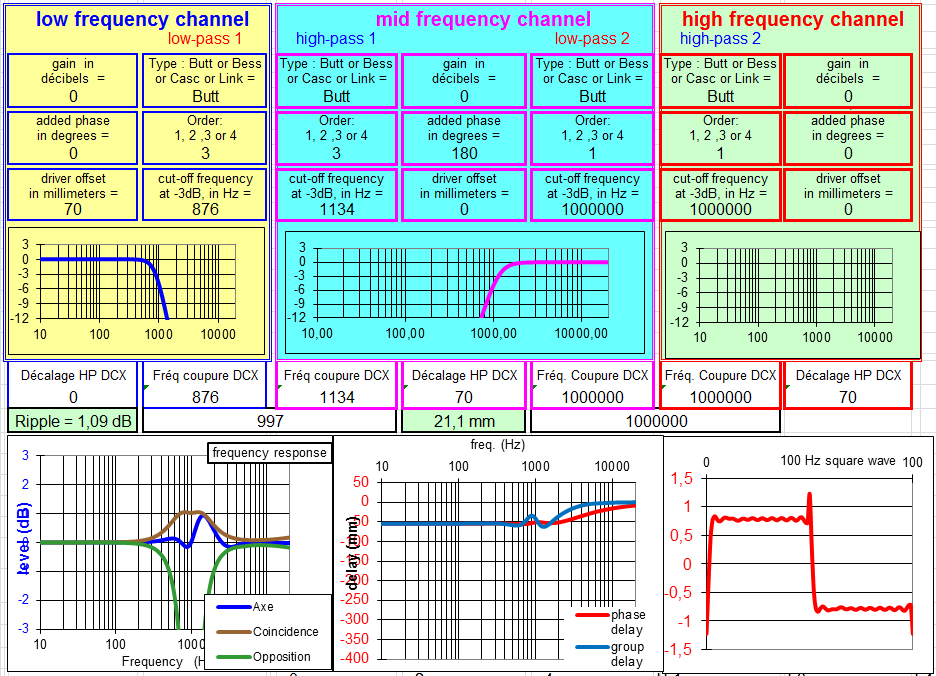
Filtre à 18 dB/octave avec raccord à -5 dB :
A l'écoute les résultats sont bons.
Je l'ai longtemps considéré comme étant le meilleurs filtre en valeur absolu, si vous avez besoin de pentes raides.
Pourtant à la simulation, et si vous pouvez vous contenter de pentes à 12 dB/octave, je pense qu'il y a mieux avec le Linkwitz Riley.
Par rapport au raccord à -3 dB, ce qui est gagné sur la courbe en coïncidence est un peu perdu sur la réponse dans l'axe et le délai de groupe.
Les filtres à 2 voies à 24 dB/octave.
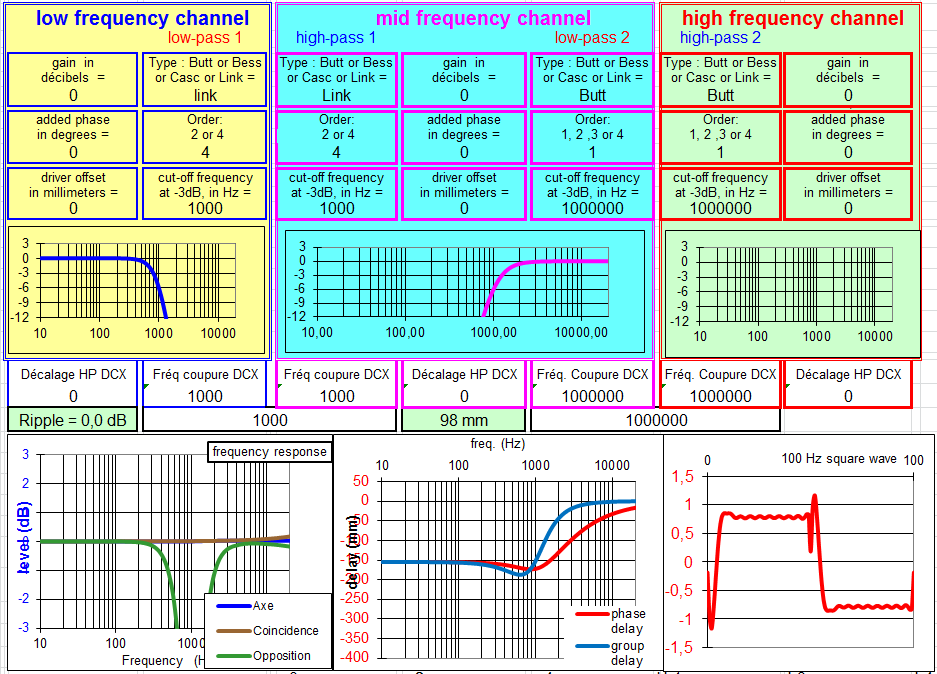
Filtre à 24 dB/octave Linkwitz Riley :
La réponse dans l'axe et en coïncidence sont pratiquement plate, les délai de phase et de groupe ont un petit accident, le signal carré est correct, pas de décalage des HP, un bon filtre facile à utiliser si vous avez besoin de pentes fortes.
Dans son livre Enceintes acoustiques & haut-parleurs, Vance Dickason écrit que c'est certainement le meilleurs filtre pour un tweeter.
Filtre à 24 dB/octave Butterworth :
Il ne faut pas couper les décibels en 4, l'accident sur la courbe de réponse dans l'axe et en coïncidence ne dépasse pas 0.5 dB.
Le décalage des fréquences de coupure est celui proposé par Vance Dickason dans son livre Enceintes Acoustiques & Haut-parleurs.
Le décalage retenu est celui qui me semble être le meilleurs, c'est assez subjectif dans ce cas.
Le filtre Linkwitz Riley est un tout petit peu meilleurs, mais c'est à écouter en pratique.
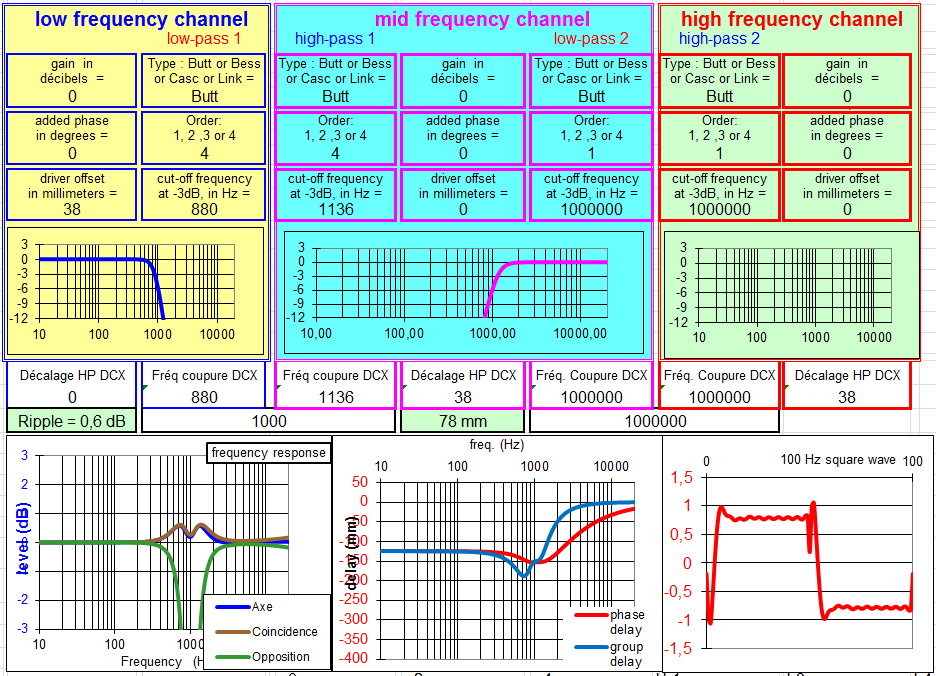
Filtre à 24 dB/octave Bessel :
Il est visiblement moins bon que le filtre Linkwitz Riley ou le Butterworth.
Il y a un décalage des fréquences de coupure, dans un sens qui peut sembler irrationnel dans le DCX.
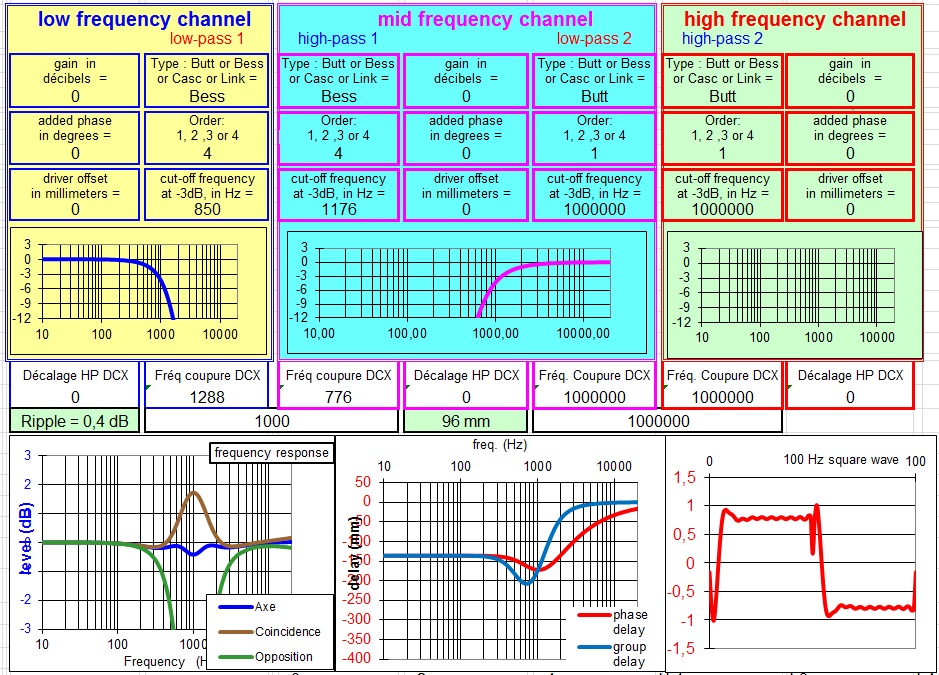
Filtre mixte à 24 dB/octave :
JMB me propose une autre solution de filtre à deux voies à pentes raides, version étudiée par Jean Michel Le Cleac'h, et reprise par plusieurs Internautes :
Outre les pentes plus accrues, cette version offre la plus grande linéarité dans l'axe et aussi la zone assimilable à une ligne à retard la plus étendue de tous les modèles de filtre quasi-optimal, avec une variation du phase délai de seulement 12 mm en comparaison normalisée ( jusqu'à 4 kHz , deux voies, Fc = 1 kHz ) alors que le 3/3 de JMLC est vers 18 mm.
Seule petite faiblesse relative étant la réponse en coïncidence.
Ce modèle est àmha à signaler et à essayer s'il y a nécessité de limiter la zone de recouvrement des HP.
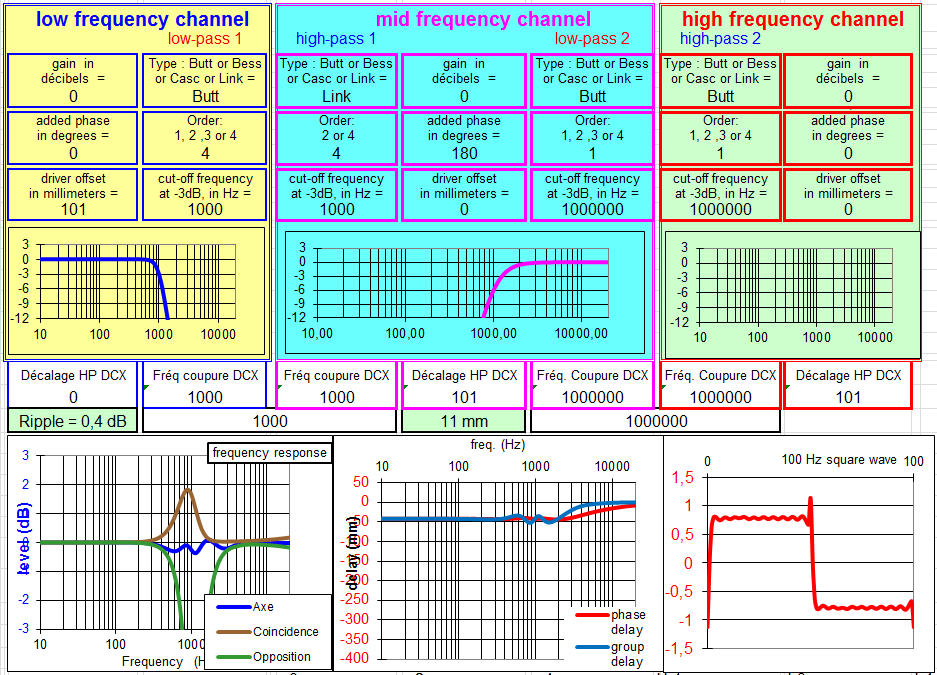
Le filtre à 2 voies à 6 et 12 dB/octave.
Filtre à 6 dB Butterworth et 12 dB Linkwitz Riley :
Je ne vous présenterai qu'une seule solution, celle qui donne les meilleurs résultats à la simulation.
La fréquence de coupure de la partie à 6 dB est décalée pour avoir un raccord à -6 dB environ à 1000 Hz.
Malgré cette correction la courbe en coïncidence n'est pas plate, la bosse est de 1 dB.
C'est mieux qu'un filtre à 6 dB pour une self de plus, avec beaucoup moins de contrainte sur le choix du tweeter.
C'est la solution de filtrage des enceintes à 2 voies économiques et performantes...
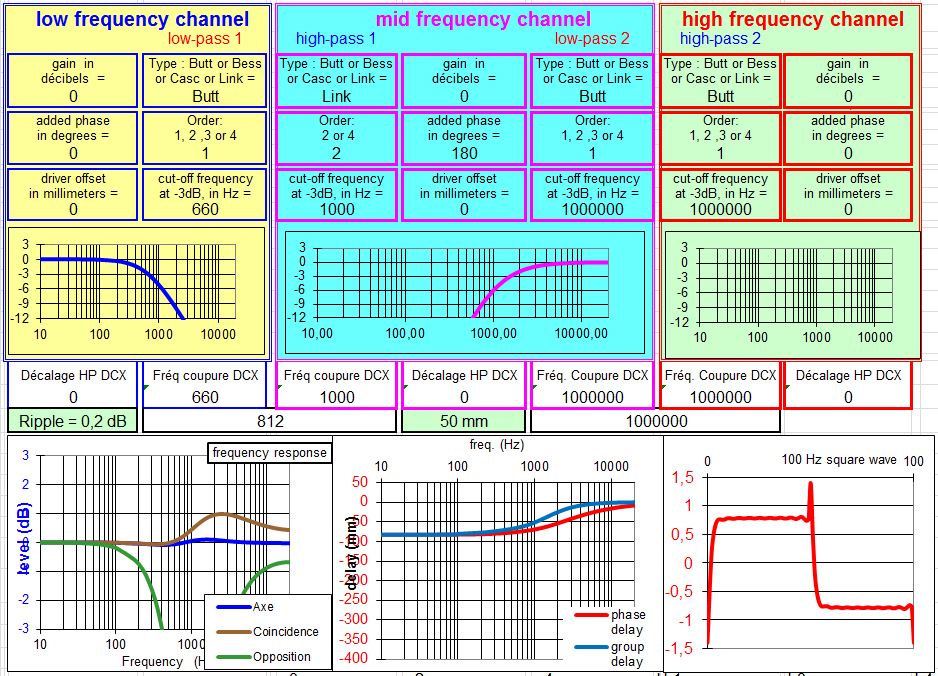
Le filtre à 2 voies à 6 et 18 dB/octave.
Filtre à 6 dB Butterworth et 18 dB Butterworth :
Je serai bref, oublions : Il n'y a rien d'intéressant de ce coté, au moins avec un filtre actif.
J'avais une idée préconçue très favorable, la simulation a battue en brèche cette idée avec une force que vous n'imaginez pas...Relativisons aussitôt :
La simulation fait l'hypothèse que les HP sont assimilabes à une résistance pure, avec une bande passante infinie et sans le moindre accident.
Or la plupart des filtres font une correction de courbe de réponse en même temps que le filtrage.
Si vous êtes dans le cas d'un grave médium dont la bande passante remonte dans le médium, et ou la self linéarise cette remontée, les conclusions de la simulation ne sont plus valables.
Avec cette mise au point, vous savez pourquoi vous pouvez tout de même l'utiliser...
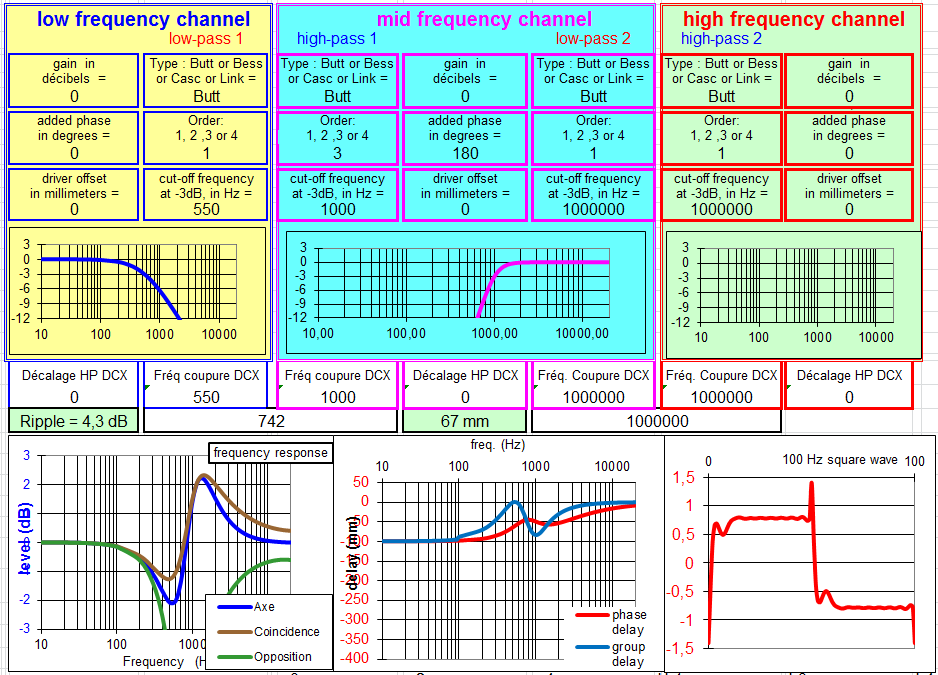
Le filtre à 2 voies à 6 et 24 dB/octave.
Filtre à 6 dB Butterworth et 24 dB :
Si vous voulez réaliser une enceinte sans avoir à déplacer le tweeter vers l'arrière, c'est le filtre qu'il vous faut, parce que c'est le grave qui doit être reculé.
Hors par construction, le grave est reculé de 30 à 50 mm par rapport au tweeter lorsqu'ils sont montés sur la même face avant.
Filtre BESSEL et tableur JMLC :
JMB écrit : Attention, il y a un gros, un très gros, piège avec les filtres BESSEL :
Sur les tableurs JLMC, la particularité est de prendre la Fc des BESSEL à -3 dB.
Cependant ces filtres sont définis en temps de propagation de groupe : " La norme définit la Fc d'un BESSEL d'ordre N comme étant la fréquence à laquelle la phase à tournée de N fois 45° ".
Exemple ci-dessous pour un BESSEL d'ordre 4.
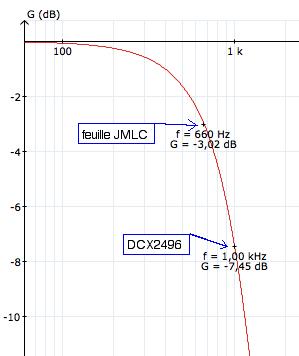
Le tableau ci-dessous permet de faire la correspondance entre les valeurs entrées dans le tableur, et les valeurs à entrer dans le filtre actif type BEHRINGER DCX 2496 :
Le passe bas est réglé à une fréquence de coupure plus haute que celle du tableur.
Le passe haut est réglé à une fréquence de coupure plus basse que celle du tableur.
Passe bas DCX Tableur JMLC Passe haut DCX Remarque BESS 2 1274 1000 785 BESS 3 1414 1000 710 N'existe pas dans le DCX BESS 4 1515 1000 660
Modification du tableur :
Par déontologie, je m'étais interdit de mettre en téléchargement une version du tableur un peu plus ergonomique et adaptée au DCX 2496.
Une discussion sur le forum MELAUDIA avec Jean Michel Le Cleac'h, message #9 à levé cette interdiction.
J'ai conservé la description des modifications pour vous montrer que je n'ai pas touché à la partie calcul et au tracé des courbes.J'ai ajouté un tableau, ligne 24 et 25, qui affiche les corrections de fréquence de coupure pour le DCX.
La case F25 contient la formule =F90, la case I25 : =I90, la case M25 : =M90 et la case O25 : = O90.
Jusque là, rien de bien compliqué...
Regardons ce qu'il y a avant la case F90 : Les cases F83 à F89.
F83 : =SI(F7="Bess";1;0) I83 : =SI(I7="Bess";1;0) M83 : =SI(M7="Bess";1;0) O83 : =SI(O7="Bess";1;0) F84 : =SI(F11=1;0;1) I84 : =SI(I11=1;0;1) M84 : =SI(M11=1;0;1) O84 : =SI(O11=1;0;1) F85 : =SI(F11=2;1.274;1) I85 : =SI(I11=2;0.785;1) M85 : =SI(M11=2;1.274;1) O85 : =SI(O11=2;0.785;1) F86 : =SI(F11=3;1.414;1) I86 : =SI(I11=3;0.710;1) M86 : =SI(M11=3;1.414;1) O86 : =SI(O11=3;0.710;1) F87 : =SI(F11=4;1.515;1) I87 : =SI(I11=4;0.660;1) M87 : =SI(M11=4;1.515;1) O87 : =SI(O11=4;0.660;1) F88 : =F83*F85*F86*F87 I88 : =I83*I85*I86*I87 M88 : =M83*M85*M86*M87 O88 : =O83*O85*O86*O87 F89 : =F15*F88 I89 : =I15*I88 M89 : =M15*M88 O89 : =O15*O88 F90 : =SI(F89=0;F15;F89) I90 : =SI(I89=0;I15;I89) M90 : =SI(M89=0;M15;M89) O90 : =SI(O89=0;O15;O89) Expliquons les choses point par point :
- Ligne 83 : Si c'est un filtre Bessel nous prenons la valeur 1, si c'est un autre filtre nous prenons la valeur 0.
- Ligne 84 :
Si c'est un filtre d'ordre 1 nous prenons la valeur 0. Si c'est un filtre d'un autre ordre nous prenons la valeur 1.- Ligne 85 :
Si c'est un filtre d'ordre 2 nous prenons la valeur du tableau, 1.274 pour un passe bas, 0.785 pour un passe haut.
Si c'est filtre d'un autre ordre nous prenons la valeur 1.- Ligne 86 :
Si c'est un filtre d'ordre 3 nous prenons la valeur du tableau, 1.414 pour un passe bas, 0.710 pour un passe haut.
Si c'est filtre d'un autre ordre nous prenons la valeur 1.- Ligne 87 :
Si c'est un filtre d'ordre 4 nous prenons la valeur du tableau, 1.515 pour un passe bas, 0.660 pour un passe haut.
Si c'est filtre d'un autre ordre nous prenons la valeur 1.- Ligne 88 : C'est la multiplication des cases 83*84*85*86.
Si c'est un filtre Bessel d'ordre 2, 3 ou 4, vous récupérez la valeur du coefficient de correction de la fréquence.
Si c'est un filtre Bessel d'ordre 1 ou un autre filtre, vous récupérez 0.- Ligne 89 : C'est la multiplication de la fréquence de coupure par le coefficient de correction.
Vous pouvez avoir 0 si vous avez 0 en 88.- Ligne 90 : Si vous avec 0 en 89 vous prenez la valeur de fréquence de coupure entrée ligne 15, si non vous prenez la valeur corrigée.
- Ligne 25 : Prend la valeur de la linge 90.
Si vous mettez la formule de la ligne 90 dans la ligne 25, vous n'avez pas besoin de la ligne 90.
Pour débugger le calcul, vous êtes bien content de l'avoir cette ligne 90.
2-6-2-8 : Réponse dans l'axe et en coïncidence :
Mise à jour : 26 décembre 2018.
Explications par Jean-Michel Le Cleac'h (JMLC) sur la réponse dans l'axe et en coïncidence, ainsi que sur les courbes de retard de groupe et de phase.
Jean-Michel nous a malheureusement quitté brutalement fin décembre 2013. Je ne le connaissais que par les forums. En hommage a sa mémoire, je maintiendrai en ligne son travail aussi longtemps que possible.
Utilisations possibles de la courbe en coïncidence
- Rayonnement des haut-parleurs d'une enceinte multivoies en phase ou pas :
Lorsque la courbe de réponse en coïncidence est confondue avec la courbe notée "axe", cela signifie une émission parfaitement en phase des haut-parleurs de l'enceinte multivoies à toute fréquence.
Cela va de pair avec un raccord à -6dB du passe-haut et du passe bas dans le filtre séparateur entre 2 voies.
Il est souhaitable, pour éviter que l'air soit brassé d'un haut-parleur à l'autre d'une enceinte multivoies que l'émission des ondes se fasse en phase d'un haut-parleur à l'autre.
On recherchera donc à ce que la courbe de réponse en coïncidence soit la plus proche possible de la courbe réponse baptisée "dans l'axe".
- Courbe de réponse en ambiance semi-réverbérante :
Lorsque l'écoute se fait en ambiance semi-réverbérante alors l'interférence entre ondes réfléchies et ondes directes peut provoquer des annulations (lorsque les ondes sont en opposition de phase) ou des renforcements (lorsque les ondes sont en phase).
La courbe de réponse mesurée en un point de la pièce montre alors des creux et des bosses.
Les sommets de ces pics sont situés sur la courbe en coïncidence et les points bas de ces creux sont situés sur la courbe en opposition.
Or, il est généralement considéré que les pics sur cette courbe de réponse en ambiance semi-réverbérante sont plus audibles que les creux.
On a donc intérêt à obtenir une courbe de réponse en coïncidence la plus plate possible.
- Contrôle des lobes de rayonnement :
Lorsqu'on se déplace devant une enceinte multivoies, les différences de marche entre les ondes directes émises par les divers haut-parleurs d'une enceinte multivoies subissent une variation, suivant certaines directions et à certaines fréquences les ondes peuvent alors être en phase, et l'intensité de la réponse sera maximale.
Ceci correspond à une ou plusieurs bosses dans la courbe en coïncidence.
L'absence de bosse sur la courbe en coïncidence permet de prévoir l'absence de lobes de rayonnement (pas de « lobing ») du au filtrage.
Courbes de retard de groupe et de phase.
Obtenues à partir de la courbe de phase ces courbes en sont d'interprétation plus facile.
Une enceinte multivoies parfaite du point de vue de la linéarité de la phase donnerait des courbes de retard de groupe et de retard de phase plates.
Hormis l'usage de filtres soustractifs ou encore de filtre du premier ordre ou encore de filtres numériques à phase linéaire, les enceintes multivoies ne sont pas à phase linéaire.
On peut appeler "distorsion de phase" cet écart à la linéarité de la phase.
Heureusement, la psychoacoustique nous apprend que du fait de la structure de notre oreille interne et de la manière dont sa membrane basilaire fonctionne, notre système auditif n'est sensible à la distorsion de phase que pour les fréquences inférieures à 4000 Hz environ.
On recherchera donc à minimiser la variation des courbes de retard de groupe et de retard de phase pour les fréquences inférieures à 4000Hz.
Pour cette gamme de fréquence on évitera toute bosse ou tout creux important dans ces courbes de de retard de groupe et de retard de phase.
Une autre explication :
Je vous propose une autre rédaction de l'explication de la réponse en coïncidence, explications à partir d'un exemple réalisé avec le simulateur en PHP, et d'images trouvées dans un forum.
Prenons un filtre deux voies à 6 dB/octave à 600 Hz, avec raccord à -3 dB.
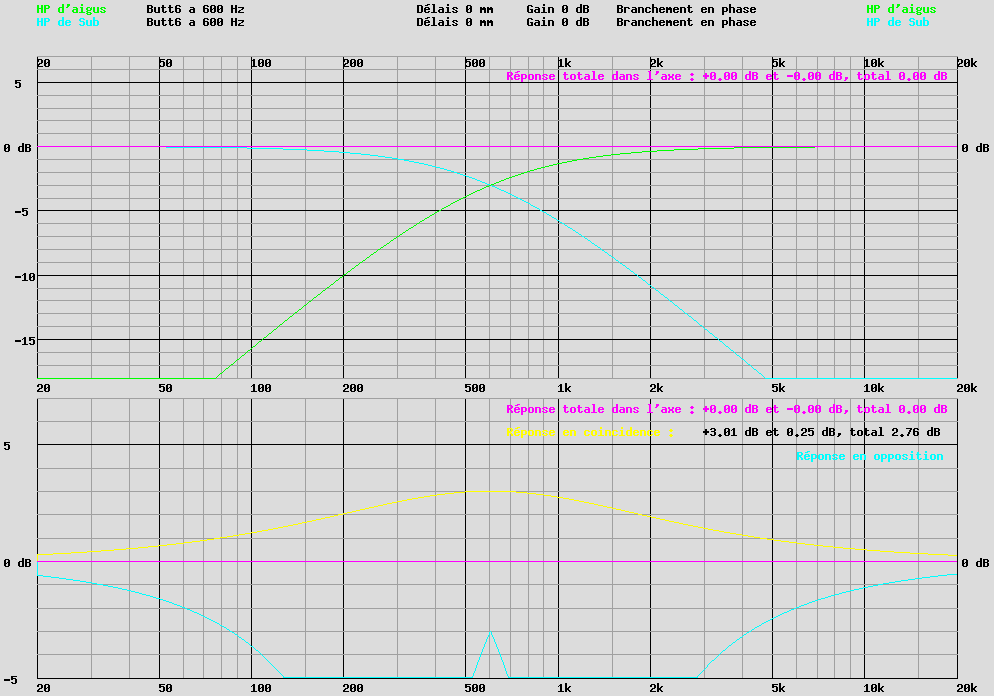
Avec un filtre à 6 dB, la courbe de réponse dans l'axe, la courbe rose, est extrêmement séduisante parce que rigoureusement plate.
Par contre la courbe de réponse en coïncidence, la courbe jaune, passe par +3 dB à la fréquence de coupure de 600 Hz.
Pour comprendre pourquoi la courbe jaune est a +3 dB, nous allons regarder comment se fait la somme des deux signaux, celui du grave et celui du tweeter, en fonction de la phase.
L'image ci-dessous est de JMB.
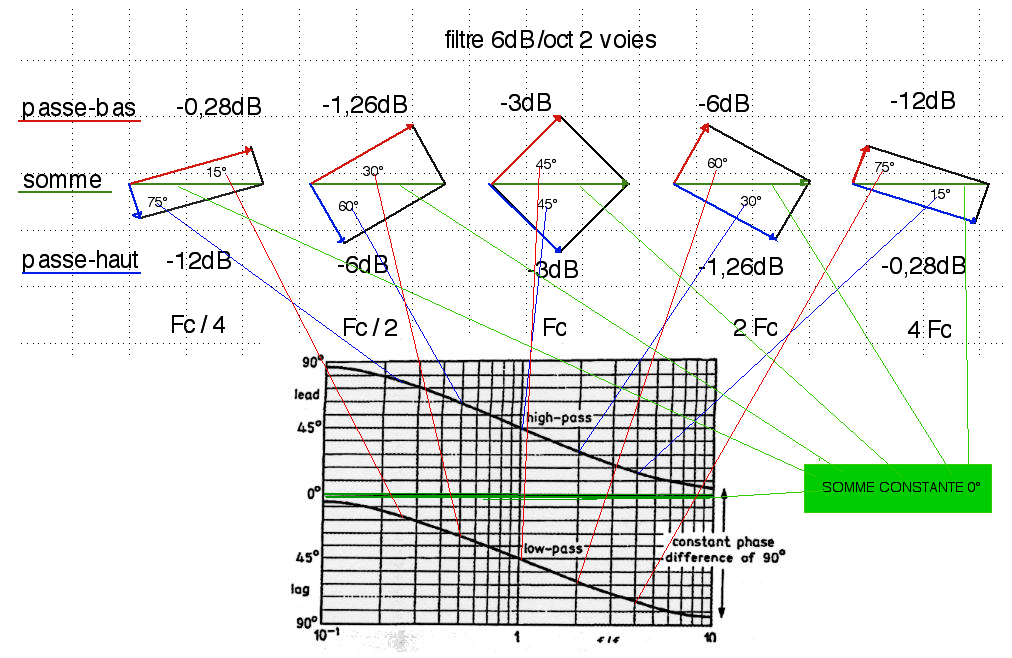
Le passe bas, c'est la réponse du grave, dont l'amplitude décroit progressivement avec la fréquence, et avec une phase qui tourne progressivement de 0° à 90°. Flèche rouge.
Le passe haut, c'est la réponse du tweeter, dont l'amplitude croit progressivement avec la fréquence, et avec une phase qui tourne progressivement de 90° à 0°. Flèche bleue.
La réponse dans l'axe, la flèche verte sur le graphique ci-dessus, est la somme vectorielle de la flèche rouge et de la flèche bleue. Elle est égale à 1 dans tout les cas, c'est à dire rigoureusement exacte au signal de départ.
Pour comprendre la réponse en coïncidence nous allons regarder de plus prés deux des sommes, celle à -3 dB et celle à -12 dB.
A 600 Hz, nous avons la réponse en coïncidence qui est égale à 20 * LOG10( 14.1421 / 10 ) = 3.01 dB.
A 2400 Hz, nous avons la réponse en coïncidence qui est égale à 20 * LOG10( 12.2474 / 10 ) = 1.76 dB.
Les deux valeurs correspondent exactement à ce qui est calculée sur la courbe jaune, la réponse en coïncidence. (LOG10 = logarithme décimal).
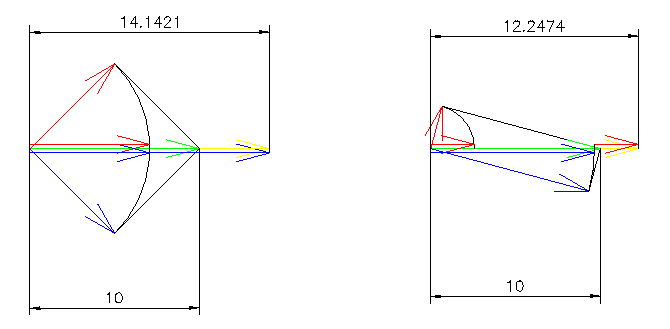
Il faut comprendre que la somme des deux signaux se fait dans l'air, entre les HP et vos oreilles.
Il y a des éléments perturbateurs, les réflexions parasites, qui peuvent changer la phase des signaux dont on souhaite écouter la somme.
Avec un système dont les délais entre les HP sont bien réglés, une mauvaise réponse en coïncidence est immédiatement audible.
Une réponse en coïncidence aussi plate que la réponse dans l'axe est un critère important de la qualité du filtre de votre enceinte.
Le filtre à 6 dB/octave n'est pas bon sur ce point, le filtre avec un HP relais est encore moins bon.
Chambre sourde ou réverbérente :
Si vous mesurez vos enceintes dans une chambre sourde, vous aurez la courbe de réponse rose.
Si vous mesurez vos enceintes dans une chambre totalement réverbérente vous aurez la courbe de réponse jaune.
Votre salon n'est ni une chambre sourde, ni une chambre totalement réverbérente, vous aurez une courbe de réponse qui va osciller entre les deux.
La réponse sera sur courbe rose a certaines fréquences, sur la courbe jaune à d'autre, et entre les deux le reste du temps.
Un accident dans la courbe de réponse théorique ne dépassera pas la courbe jaune, mais pourra l'atteindre ponctuellement.Maintenant si vous prenez un filtre Linkwitz-Riley par exemple, les deux courbes rose et jaune sont parfaitement confondues.
Une enceinte avec les courbes rose et jaune confondues sont donc beaucoup moins sensible à l'acoustique de la pièce d'écoute.
La phase des filtres Linkwitz-Riley est corrigeable par convolution.
Vous pouvez avoir une courbe de réponse sans problème dû à la pièce et une réponse sur les signaux carrés très proche de l'idéal théorique.
Je me demande pourquoi ces filtres associés à la correction par convolution ne sont pas plus utilisés.
Une solution très efficace :
Si vous avez utilisé un peu le simulateur de filtres théoriques JMLC, vous vous êtes rendu compte qu'il y avait deux cas :
- Si la réponse en coïncidence est bonne, la réponse sur un signal carré est mauvaise.
- Lorsque la réponse sur un signal carré est bonne, la réponse en coïncidence est mauvaise.
Vous pouvez prendre les simulations comme vous voulez, vous serez toujours dans l'un des deux cas.
Il y a pourtant une porte de sortie par le haut, la correction de la phase acoustique.
Avec cette correction, vous avez les pentes raides qui sont nécessaires à un bon raccordement des HP entre eux, et une réponse sur un signal carré parfaite.
Dit autrement, vous passez d'un filtre IRR avec tout les défauts qui vont avec, à un filtre FIR linéaire en phase.
A l'écoute il n'y a pas photo, essayer la correction de la phase acoustique c'est l'adopter.
Avec cette correction ne cherchez plus les filtres qui conviennet : Les Linkwitz Riley a 12, 24 ou 48 dB/octave sont les meilleurs, raccordement à -6 dB, réponse linéaire dans l'axe.
Un petit coup de patte au passage à nos chers Audiophiles aux oreilles d'or : Leur filtre préféré, le filtre à 6 dB/octave, est mauvais sur la courbe de réponse en coïncidence.
Je suis très surpris qu'avec leurs oreilles d'or ils ne l'aient pas entendu.
Un grand merci pour votre visite. --- Retour direct en haut de la page ---
Un grand-père facétieux disait à ses petits enfants que le grand truc blanc tout en haut du Puy-de-Dôme était un thermomètre géant : Quand il deviendra tout rouge il faudra vite se sauver, parce que le volcan va se réveiller !!!
Dôme Acoustique
Malgré les apparences, ce site internet n'est que celui d'un amateur passionné auvergnat.
"Amateur" doit être compris dans le sens "non professionnel", dans l'aspect financier de l'approche : Je ne vis pas des revenus de cette passion.
"Amateur" doit être compris dans le sens ou rien ne m'oblige à vous répondre, si vous êtes désagréable. C'est rare, mais le cas arrive de temps en temps.
Il y a un savoir-vivre élémentaire qui consiste à demander l'autorisation avant de reprendre tout ou partie de ce qui est écrit dans ce chapitre.
Je vous donnerai l'accord, demandez-le simplement pour être en règle. Sont exclues les demandes extravagantes.
Contrôle de validation W3C du code HTML 5 de la page, copiez l'adresse de la page avant de cliquer sur le lien.
Contrôle de validation W3C des CSS de la page, copiez l'adresse de la page avant de cliquer sur le lien.
Ce sont deux outils de contrôle pour le webmaster du site Dôme Acoustique, c'est inutile pour les utilisateurs.
Avoir le lien dans chaque page est plus simple pour les retrouver.