| Page affichée à 13:05:20 samedi 21 décembre 2024 Ce site n'utilise pas de cookie |
 |
Dôme acoustique | Compteur pour tout le site : 17 184 752 Nombre actuel de lecteurs : 396 Les menus pour smartphone. |
Faire un don par PayPal |
| Le site de Dominique, un amateur passionné |
2-3-1-4 : Le report des surfaces
Mise à jour : 11 mars 2023, Antidote 11.
Définition :
Un pavillon c'est au départ une loi d'expansion, loi qui définit quelle doit être la surface à une distance donnée.
Cette loi d'expansion, le plus souvent hyperbolique, n'est un secret pour personne, les formules sont dans le site, et il y a un calculateur en ligne pour avoir les résultats.
La loi exponentielle est un cas particulier des lois hyperbolique, obtenue avec T = 1.000.À côté de cette loi d'expansion, il y a le report des surfaces dans le plan, sous la forme d'un diamètre, ou d'une largeur et d'une hauteur, pour avoir la définition exacte des bords du pavillon.
Ce report peut se faire avec une surface plane, sphérique, cylindrique, JMLC, ou deux autres solutions que je vous proposerai.
À partir de la même loi d'expansion, en fonction du report que vous allez faire, vous n'aurez pas le même pavillon, vous n'aurez pas la même sonorité.Ce que j'appelle le report des surfaces, c'est la façon dont nous allons transformer une surface mathématique en un tracé sur le plan, pour définir les bords du pavillon.
Nous allons voir quelles propriétés il faut à cette surface, pour faire un pavillon correct.
Vous vous rendrez compte qu'entre "les grandes idées" et la simulation, il y a un monde entre les deux.
Si vous n'allez pas au bout "des grandes idées", vous ne savez pas qu'elles ne sont pas bonnes.
Méthode :
Nous allons partir sur une loi d'expansion hyperbolique à 350 Hz, pour une compression de 2", avec un T = 0.707.
C'est la solution qui permet d'avoir une coupure à 1.5 fois la fréquence de calcul, 525 Hz dans notre cas.
Nous allons tracer 5 pavillons :
- Le premier avec l'hypothèse d'une surface plane.
- Le second avec l'hypothèse d'une surface sphérique concentrique.
- Le troisième avec l'hypothèse d'une surface JMLC.
- L'hypothèse du quatrième sera expliquée le moment venu, après la critique des trois premières hypothèses.
- Le cinquième est une extrapolation du quatrième, avec une surface sphérique non concentrique, ou une surface en ellipsoïde.
Pour simplifier les tracés, nous allons partir sur un pavillon circulaire.
C'est la raison pour laquelle l'hypothèse de la loi d'expansion cylindrique ne sera pas tracée, cette loi ne s'applique pas aux pavillons circulaires.Pour ne pas donner prise à la critique, chaque pavillon a été tracé avec une précision de 0.001 mm sur toutes les distances.
En faisant ainsi nous sommes certains qu'une valeur annoncée à 0.1 mm prés est juste, et ne peut pas être remise en cause.
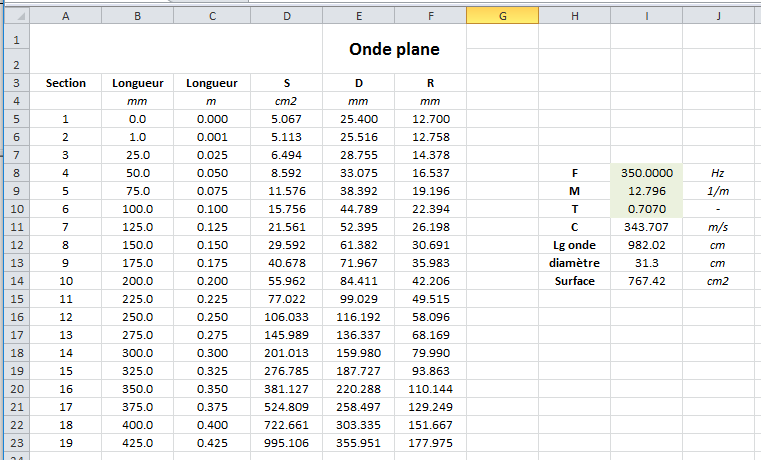
Le contrôle se fait en divisant chaque section en 5 parties, en reliant les points entre eux, et en mesurant les longueurs de chacune des lignes, les lignes sont équidistantes entre elles.
La vitesse de l'air étant constante, un pavillon idéal devrait avoir toutes les lignes d'écoulement de la même longueur.
Nous en sommes loin pour les premières formes de surface...Les lignes d'écoulement c'est un peu le découpage du pavillon en plusieurs parties, pour en faire un pavillon sectoriel.
Dans le cas présent les secteurs sont ronds, alors que sur les réalisations commerciales les secteurs sont carrés ou rectangulaires.
Tout comme le nombre de secteurs n'est pas limité, le nombre de lignes d'écoulement peut être choisi comme nous le voulons, c'est le temps de tracé qui fait que l'on se limite à 4, 5, 10 ou 12 lignes d'écoulement.
Pavillon avec des surfaces plates :

Longueur du pavillon : 350.0 mm. Diamètre du pavillon : 440.6 mm.
Le pavillon à surfaces plates est le plus simple à tracer, le calcul peut facilement être fait dans un tableur.
Contrôle du pavillon à surfaces plates ci-dessus.
- Longueur sur l'axe : 350.0 mm.
- Longueur : 353.0 mm.
- Longueur : 361.8 mm.
- Longueur : 375.4 mm.
- Longueur : 393.1 mm.
- Longueur le long du pavillon : 414.0 mm.
Différence entre la longueur maxi et la longueur mini = 64.0 mm.
Cette forme de surface n'est pas bonne du tout. Erreur 18%.
Pavillon avec des surfaces sphériques concentriques :

Longueur du pavillon : 308.7 mm. Diamètre du pavillon : 433.0 mm.
Contrôle du pavillon à surfaces sphériques concentriques ci-dessus.
- Longueur sur l'axe : 350.0 mm.
- Longueur : 351.4 mm.
- Longueur : 355.7 mm.
- Longueur : 362.4 mm.
- Longueur : 371.4 mm.
- Longueur le long du pavillon : 382.4 mm.
Différence entre la longueur maxi et la longueur mini = 32.4 mm, la moitié du pavillon à surfaces plates.
Cette forme de surface n'est pas bonne du tout. Erreur 9%.En partant avec une surface sphérique nous aurions pu penser que toutes les longueurs seraient égales.
Cela aurait été le cas pour un pavillon conique or nous avons un pavillon dont les sections croissent progressivement.
Le trait mixte dans le pavillon a rigoureusement la même longueur que sur l'axe.
Nous voyons bien l'angle que prennent les lignes d'écoulement, et donc les longueurs plus importantes.Nous voyons aussi que le pavillon à surfaces sphériques concentriques est plus court que le pavillon à surfaces plates.
Pourtant, la loi d'expansion est identique.
C'est la combinaison d'une loi d'expansion et d'une forme de surface qui permet de tracer un pavillon.
Il reste à trouver quelle est la bonne forme de surface qui donne des lignes d'écoulement toutes de même longueur.
Nous avons progressé, mais nous n'y sommes toujours pas.
Pavillon avec des surfaces JMLC :
La caractéristique des surfaces JMLC est d'arriver perpendiculairement aux parois du pavillon, comme pour un pavillon Tractrix.
Je n'ai pas d'idée préconçue sur les résultats de ce pavillon, contrairement à ceux à surfaces plates ou sphériques.
La première section au niveau de la gorge est rigoureusement identique à celle d'un pavillon à surfaces sphériques, la différence se fait de plus en plus en avançant vers la bouche.
Habituellement ces pavillons sont calculés avec un outil sous EXCEL. La méthode graphique y arrive aussi très bien, avec un peu de savoir-faire...

Longueur du pavillon : 276.2 mm. Diamètre du pavillon : 393.3 mm.
Contrôle du pavillon à surfaces JMLC ci-dessus.
- Longueur sur l'axe : 350.0 mm.
- Longueur : 351.5 mm.
- Longueur : 355.5 mm.
- Longueur : 359.5 mm.
- Longueur : 360.5 mm.
- Longueur le long du pavillon : 350.0 mm.
De par la méthode de tracé du pavillon, il est tout à fait normal que la longueur le long du pavillon soit identique à la longueur sur l'axe.
Par contre sur les lignes d'écoulement intermédiaires nous avons 10.5 mm de différence. Erreur de 3%.
Ce pavillon à la réputation d'être bon à l'écoute, l'analyse des lignes d'écoulement le prouve.
Il est possible de faire encore mieux, ce que je vais vous proposer ci-dessous.La raison qui fait que le pavillon à surfaces JMLC n'est pas bon au niveau des lignes d'écoulement vient que la croissance des sections se fait uniquement par le bord des sections.
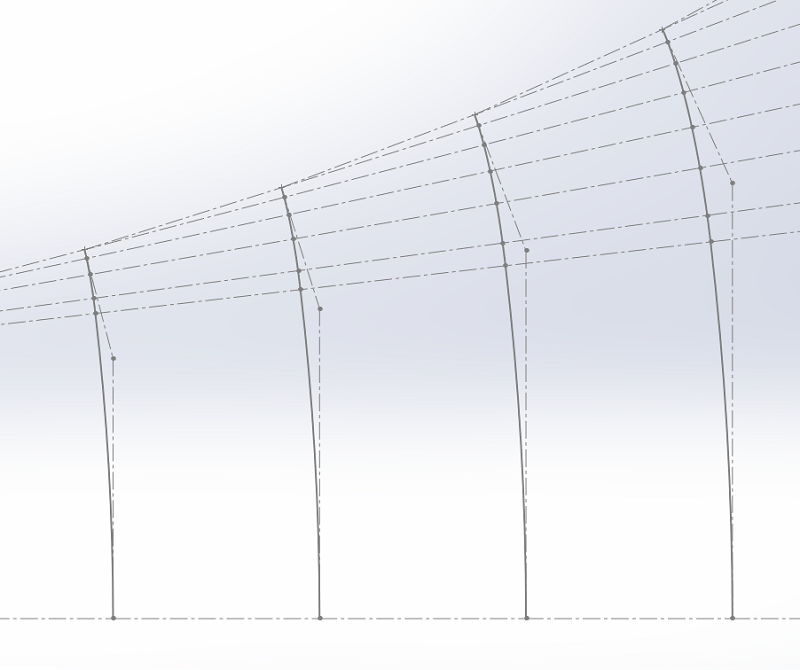
Or les lignes d'écoulements s'écartent de façon équidistante entre le centre et le bord.
La croissance du pavillon ne se fait pas au bon endroit.
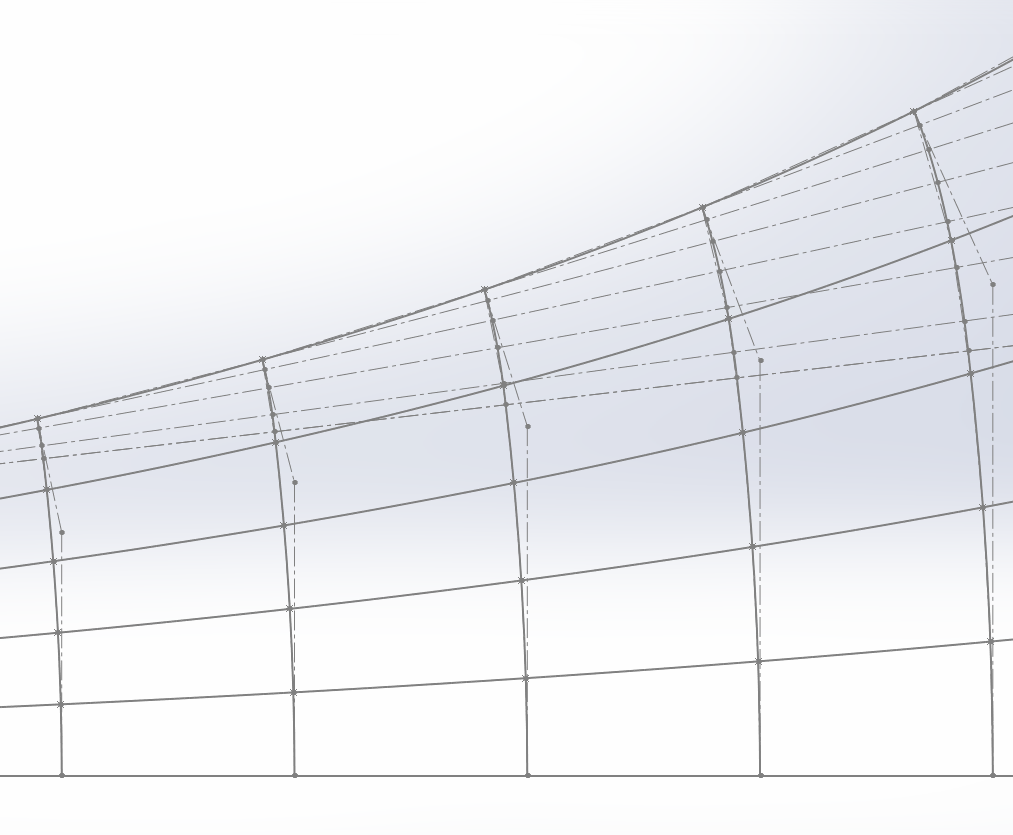
C'est surtout vers la bouche que la différence entre la croissance du pavillon et les lignes d'écoulement saute aux yeux.
Les lignes d'écoulement croisent les lignes de construction avec un angle, donc les longueurs sont différentes.
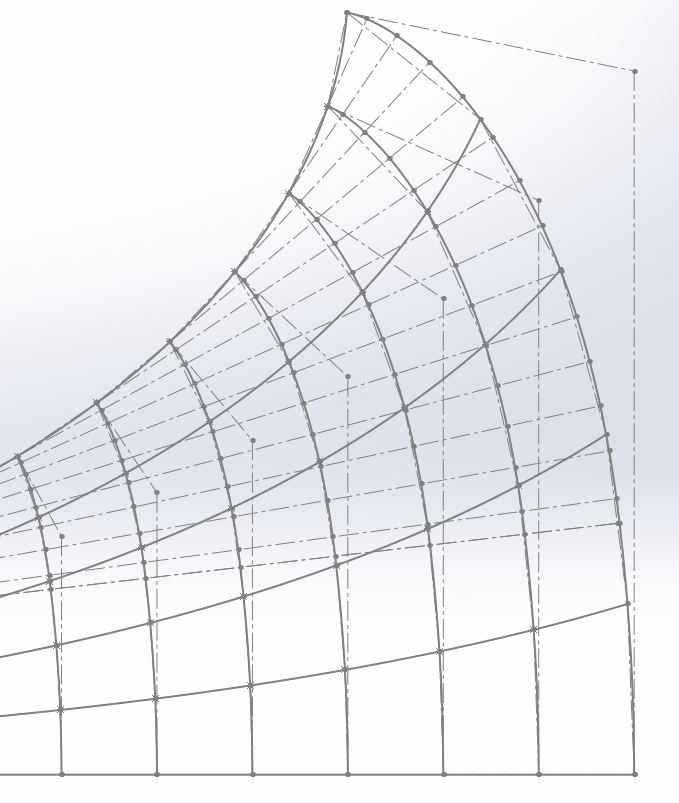
Pavillon avec des surfaces temporelles :
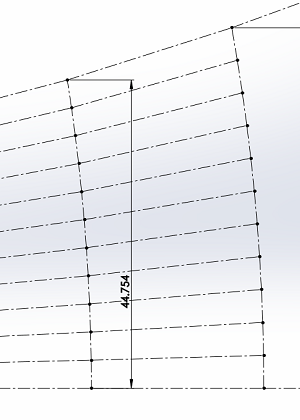
Trois règles de construction :
- Les 12 lignes horizontales ou presque horizontales entre deux sections sont de longueur égale.
- Les 11 lignes verticales ou presque verticales qui définissent une section sont de longueur égale.
- La côte de rayon est choisie pour obtenir la surface voulue, surface de révolution qui passe par les 12 points aux extrémités des lignes verticales ou presque verticales.
Le nombre de lignes d'écoulement est choisi pour avoir une précision suffisante sur les grandes surfaces, vers la bouche du pavillon.
Avec ces trois règles, les distances entre les lignes d'écoulement sont identiques, la longueur des lignes d'écoulement est identique.
Ce sont les propriétés que nous voulions obtenir, la méthode de tracé retenue permet de l'obtenir directement.Nous pouvons expliquer les choses autrement :
La surface est définie par les points qui sont atteint au même temps depuis la source, avec une répartition uniforme sur la surface.
La vitesse de l'air étant constante, parler de temps en ms ou de distance en mm entre deux sections, est identique.
Le nom temporel vient de cette notion de temps constant sur toutes les surfaces.

Longueur du pavillon : 267.1 mm. Diamètre du pavillon : 406.1 mm.
Le pavillon à surfaces temporelles est à la fois plus court et plus grand en diamètre que le pavillon à surfaces JMLC.
Contrôle du pavillon à surfaces temporelles ci-dessus :
De par sa méthode de construction, qui est identique à celle de contrôle, il y a 0% d'erreur en tout point. Erreur 0%.
Seule une écoute peut valider, ou invalider, l'hypothèse utilisée pour le contrôle. Nous parlons de 3% de différence avec les surfaces JMLC.
Un contrôle du pavillon IWATA avec cette méthode sera également réalisé.
Pavillon avec des surfaces sphériques non concentrique :
Sur le pavillon à surfaces équidistantes le long des lignes d'écoulement, j'ai fait passer un cercle dont le centre se trouve sur l'axe horizontal, dont un point se trouve lui aussi sur l'axe horizontal à la distance 350 mm, et dont un autre point se trouve sur le dernier point de définition de la section, le plus éloigné de l'axe.
Nous nous rendons compte sur l'image ci-dessous que ce cercle est pratiquement superposé à la surface équidistantes le long des lignes d'écoulement, avec une erreur de 1.66 mm, c'est-à-dire environ 1% sur 350 mm. Erreur 1%.
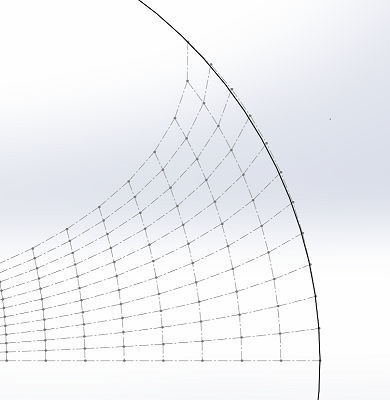
Cinq règles de construction :
- Le centre du cercle se trouve sur l'axe horizontal.
- Un point du cercle se trouve sur l'axe horizontal à la distance souhaitée.
- Un autre point du cercle se trouve sur le profil du pavillon.
- La longueur horizontale et la longueur le long du profil du pavillon sont rigoureusement identiques.
- La côte de rayon est choisie pour obtenir la surface voulue.
Comme pour le pavillon à surfaces équidistantes le long des lignes d'écoulement, nous oublions toutes les notions de perpendicularité entre les surfaces sphériques non concentriques et le profil du pavillon.
Je n'irai pas plus loin, 1% d'erreur est de trop lorsque l'on sait faire facilement 0%.
Pavillon avec des surfaces en ellipse de révolution non concentrique :
Sur le pavillon à surfaces équidistantes le long des lignes d'écoulement, j'ai fait passer une ellipse dont le centre se trouve sur l'axe horizontal, dont un point se trouve lui aussi sur l'axe horizontal à la distance 350 mm, et dont un autre point se trouve sur le dernier point de définition de la section, le plus éloigné de l'axe, et dont un 3e point se trouve au bout d'une ligne d'écoulement vers le milieu de chaque section.
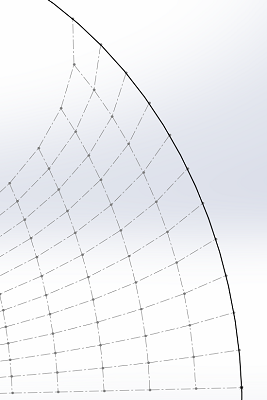
Six règles de construction :
- Le centre de l'ellipse se trouve sur l'axe horizontal.
- Un 1er point de l'ellipse se trouve sur l'axe horizontal à la distance souhaitée.
- Un 2e point de l'ellipse se trouve sur le profil du pavillon.
- Un 3e point de l'ellipse se trouve sur la ligne d'écoulement placée entre les deux premières lignes.
- La longueur horizontale, la longueur le long du profil du pavillon, la longueur de la ligne d'écoulement sont rigoureusement identique.
- La côte de rayon est choisie pour obtenir la surface voulue.
Comme pour le pavillon à surfaces équidistantes le long des lignes d'écoulement, nous oublions toutes les notions de perpendicularité entre les surfaces en portion d'ellipse de révolution non concentrique et le profil du pavillon.
C'est cette méthode qui va être utilisée maintenant pour reconstruire un pavillon et mesurer les erreurs, avec juste une ligne d'écoulement centrée et des surfaces qui sont des portions d'ellipses de révolution.


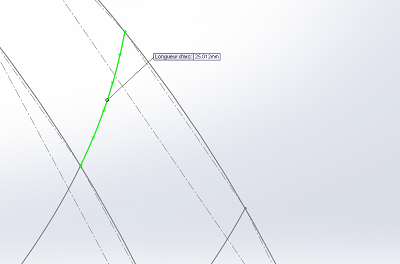
Contrôle sur une section du pavillon.
Nous devrions avoir 25 mm, nous en avons 25.012 mm, soit 0.048%, l'approximation du tracé.
Un peu plus loin j'ai mesuré 25.017 mm, ce qui ne change rien de significatif.
Surfaces temporelles ou surfaces en ellipse de révolution non concentrique sont rigoureusement équivalentes.
Le test du candide :
Comment choisir entre surfaces JMLC et surfaces temporelles ?
J'ai montré les images des méthodes de tracé à ma fille, 25 ans, qui ne connaît rien à la hi-fi et au calcul des pavillons.
Ma fille à fait un IUT Génie mécanique, donc elle connaît la CAO et le dessin industriel, suivit d'une école d'ingénieur textile, l'ENSAIT à Roubaix : C'est une tête bien faite !!!La conclusion est tombée très vite, ce sont les surfaces temporelles, qui restent parallèles entre elles en tout point, qui sont les plus logiques.
Vous approuverez ou pas cette conclusion, qui a au moins le mérite d'exister.
Et avec Hornresp ?
Hornresp est un logiciel de simulation des pavillons, dont les résultats m'ont sérieusement ébranlé, parce qu'ils ne sont pas en accord avec les parties précédentes du chapitre.
Entre des théories plus ou moins justes, et une simulation avec un logiciel qui a fait ses preuves, la vérité est la simulation...
La mode d'emploi de Hornresp en téléchargement, parce qu'il ne faut pas le perdre, et qu'il est trop gros pour être affiché dans le chapitre.
Comparaison entre les surfaces planes et sphériques :
| La loi d'expansion est exponentielle, calculée à 250 Hz. Les surfaces des sections droite ou sphérique sont rigoureusement identiques. Le profil du pavillon avec des surfaces sphériques est plus court que celui avec des surfaces planes |
|
 |
|
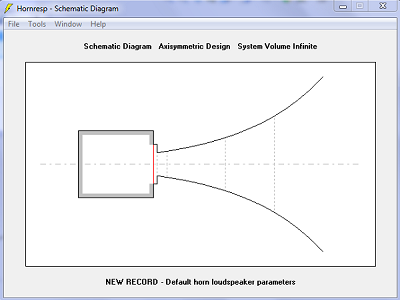
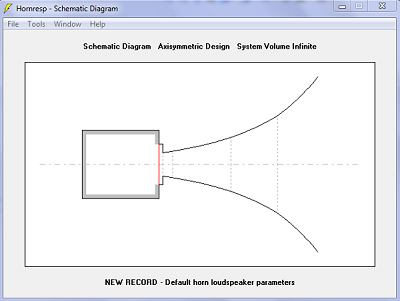
| Surfaces droites | Surfaces sphériques |
| Paramètres de calculs. | |
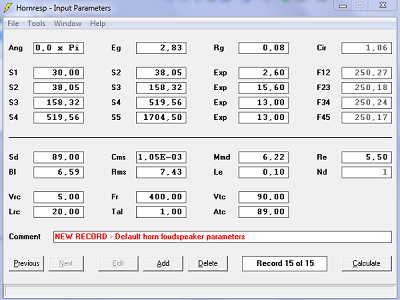 |
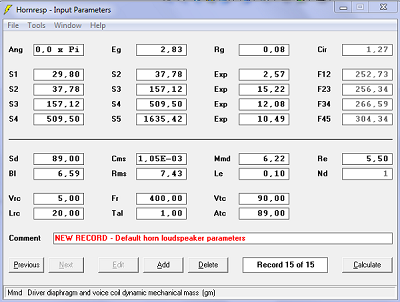 |
| Diagramme schématique. Les différences ne sont pas visibles. | |
 |
 |
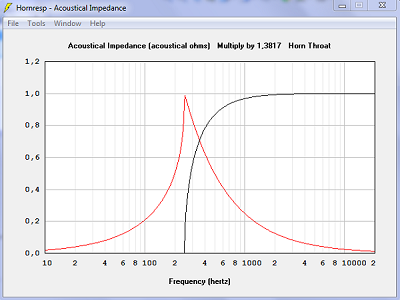
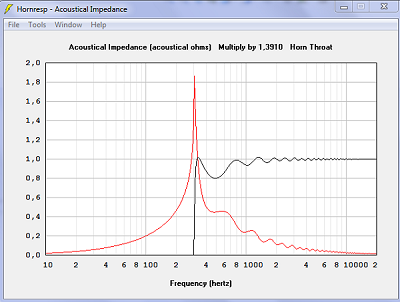
| Impédance acoustique en noir. L'impédance est parfaite avec des surfaces droites, plus ondulée avec des surfaces sphériques. Réactance en rouge. Le maximum est plus haut donc moins bon, 1.9 au lieu de 1.0, avec les surfaces sphériques. |
|
 |
 |
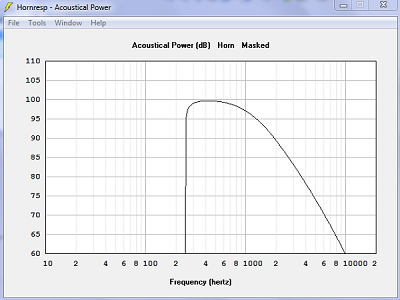
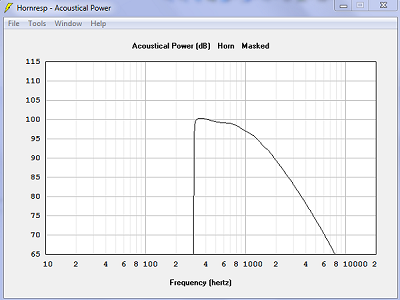
| Puissance acoustique. C'est un peu moins bon avec des surfaces sphériques. | |
 |
 |
| Impédance électrique. À part l'accident à 250 Hz avec les surfaces planes, à 300 Hz avec les surfaces sphériques, c'est identique. | |
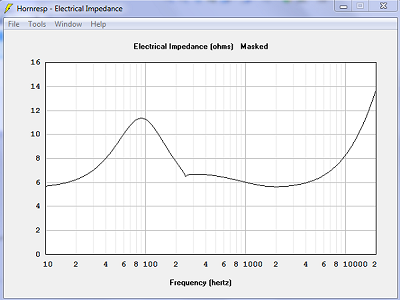 |
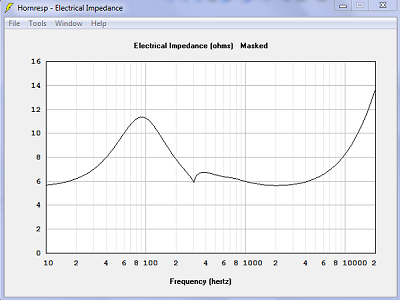 |
| Déplacement de la membrane. À part l'accident à 250 Hz avec les surfaces planes, à 300 Hz avec les surfaces sphériques, c'est identique. | |
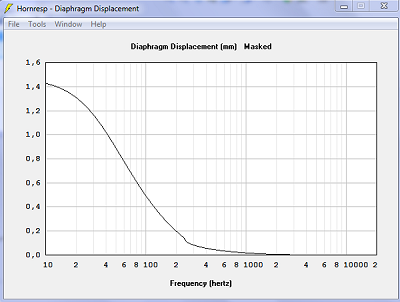 |
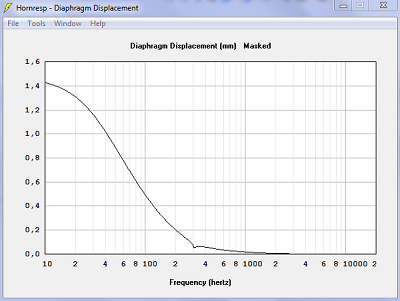 |
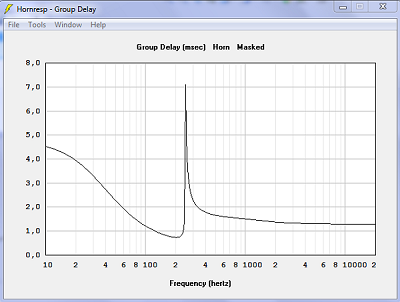
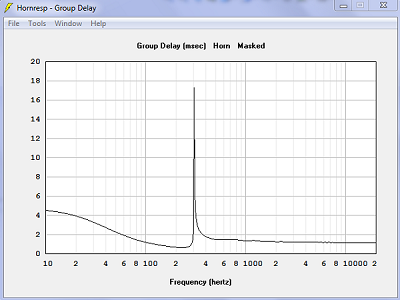
| Délai de groupe. Le maximum est plus de deux fois plus haut, 17.5 ms au lieu de 7.2 ms, avec les surfaces sphériques. | |
 |
 |
| Pourquoi passer du temps à la CAO à dessiner des surfaces qui sont moins bonnes à la simulation ? Il faut reconnaître les évidences de la simulation, les surfaces droites avec une loi d'expansion exponentielle sont les meilleures. |
|
Comparaison entre les surfaces planes et temporelles :
| La loi d'expansion est exponentielle, calculée à 250 Hz. Les surfaces des sections droites ou temporelles sont rigoureusement identiques. Le profil du pavillon avec des surfaces temporelles est plus court que celui avec des surfaces planes ou sphériques |
|
 |
|
| Surfaces droites | Surfaces temporelles |
| Paramètres de calculs. | |
 |
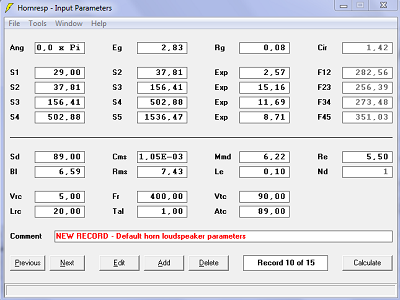 |
| Diagramme schématique. Les différences ne sont pas visibles. | |
 |
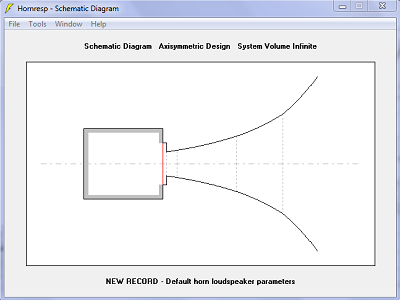 |
| Impédance acoustique en noir. L'impédance est parfaite avec des surfaces droites, une énorme pointe avec des surfaces temporelles. Réactance en rouge. Le maximum est beaucoup plus haut, donc moins bon, 3.5 au lieu de 1.0, avec les surfaces temporelles. J'ai bien tout vérifié, il n'y a pas de bug. |
|
 |
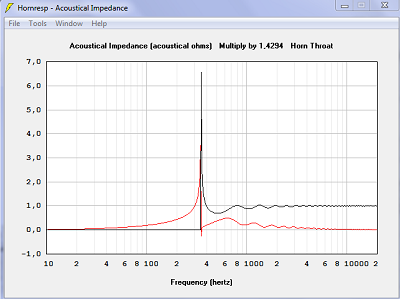 |
| Puissance acoustique. C'est moins bon avec des surfaces temporelles. | |
 |
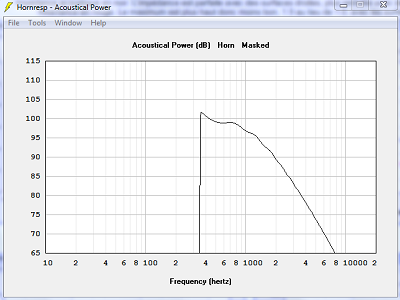 |
| Impédance électrique. À part l'accident à 250 Hz avec les surfaces planes, à 350 Hz avec les surfaces temporelles, c'est identique. | |
 |
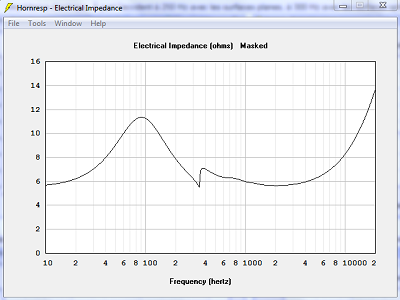 |
| Déplacement de la membrane. À part l'accident à 250 Hz avec les surfaces planes, à 350 Hz avec les surfaces temporelles, c'est identique. | |
 |
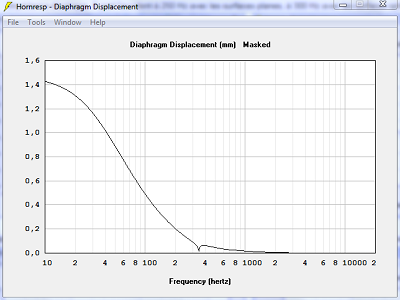 |
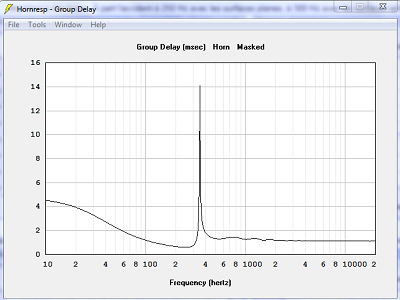
| Délai de groupe. Le maximum est plus de deux fois plus haut, 14.0 ms au lieu de 7.2 ms, avec les surfaces temporelles. | |
 |
 |
| Pourquoi passer du temps à la CAO à dessiner des surfaces qui sont moins bonnes à la simulation ? Il faut reconnaître les évidences de la simulation, les surfaces droites avec une loi d'expansion exponentielle sont les meilleures. |
|
Changeons d'approche :
Le dessin ci-dessous fait correspondre exactement le profil des pavillons à surfaces planes et temporelles.
La question est : quelle est la loi d'expansion du pavillon à surfaces temporelles ?

La CAO va permettre de mesurer chaque surface et longueur du pavillon à surfaces temporelles, avant de rentrer les valeurs dans un tableur EXCEL.
Les surfaces planes sont calculées avec une loi d'expansion avec F = 250 Hz et T = 1.000.Les surfaces temporelles calculées avec F = 198 Hz et T = 1.575 correspondent exactement en trois points, au début, vers le milieu et à la fin, et ne sont pas justes ailleurs.
Les erreurs ne dépassent pas ±0.3 mm au rayon sur mon exemple, qui est capable de réaliser un pavillon de façon aussi précise ?
Maintenant, avec un T = 1.575, la simulation Hornresp ne sera jamais bonne, la solution est à oublier au plus tôt.Les surfaces temporelles calculées avec F = 225 Hz et T = 1.000 correspondent exactement en deux points au début et à la fin, et ne sont pas justes ailleurs.
L'erreur maximum atteint +1.012 mm au rayon, au 3/4 de la longueur, toutes les erreurs sont du même côté.
Bien sûr, on pourrait dire que 1 mm d'erreur sur un rayon de 150 mm ce n'est pas grand-chose, mais je refuse de tricher à ce point.
Conclusions :
Je ne vais pas me prendre la tête, les surfaces planes sont les meilleures, ce sont aussi les plus simples à tracer, je vais oublier le reste.
J'étais pourtant assez fier de mes surfaces temporelles, Hornresp en a fait qu'une bouchée, c'est la réalité d'une étude...
À l'avenir je ne parlerai que de surfaces planes...
Pavillon à surfaces temporelles et JMLC à la limite:
Le but est simplement d'augmenter la longueur pour voir le comportement du pavillon aux très grandes longueurs, que personne n'utilise.
Deux pavillons sont comparés, le JMLC qui a la côte auprès des audiophiles, et le temporel que je propose.
Aucun des deux n'est satisfaisant aux grandes longueurs, aucun des deux ne montera sur le podium !!!
Je rappelle simplement que nous sommes à plus de quatre fois la longueur qui est nécessaire pour reproduire correctement la fréquence limite basse du pavillon, personne ne réalise un pavillon aussi long.
Le pavillon JMLC à la limite :
La limite se voir du premier coup d'œil, personne ne peut contester ce point.
Les surfaces qui passent à l'arrière du pavillon m'ont toujours semblé surréalistes.
Tel que sont construites les surfaces, le passage à l'arrière du pavillon est la conséquence des règles utilisées pour tracer les surfaces.

Le pavillon à surfaces temporelles à la limite :
La limite se trouve sur le dessus du pavillon, quand la surface arrive tangente avec le bord du pavillon.
La surface me semble plus réaliste que celle du pavillon JMLC.

Comparaison en 3D des pavillons à surfaces temporelles et JMLC à la limite :
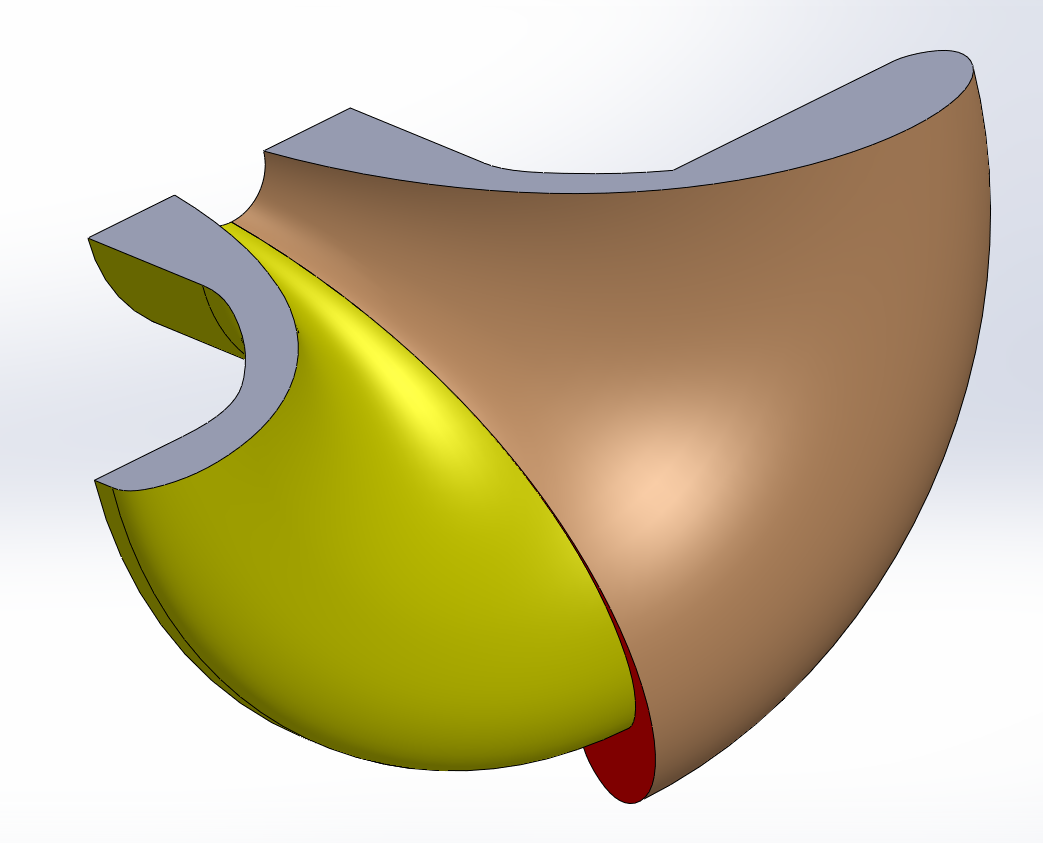
La différence est peu importante sur la partie utile d'un pavillon capable de descendre à 350 Hz.
En traçant les pavillons à la limite, je suis, sur le pavillon à surfaces temporelles, à 3 fois la surface nécessaire.
Si je raccourcissais les deux pavillons pour une surface de 800 cm2 environ, la différence serait plus faible.
Deux méthodes de tracés différentes qui donnent presque le même résultat pratique dans la zone de surface utile, il faut comprendre ce petit miracle !!!
La superposition des esquisses va nous expliquer les choses.
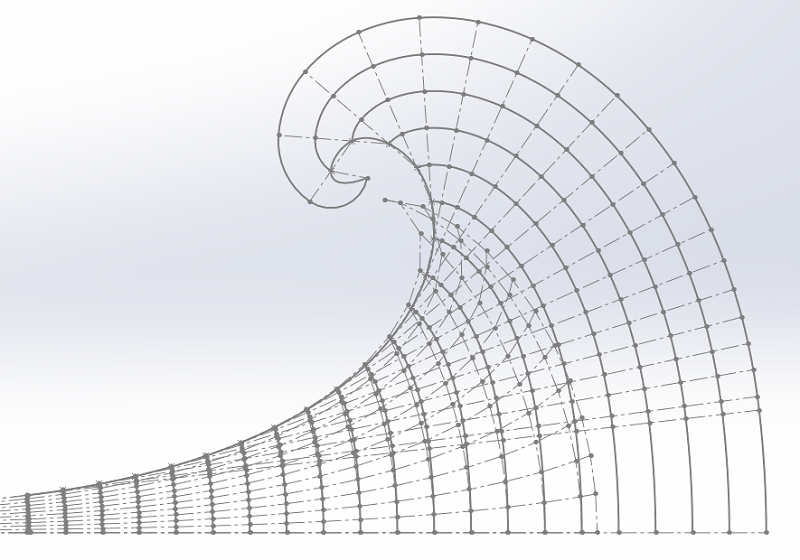
Un zoom est nécessaire pour bien voir la différence.
La dernière surface complète fait 807 cm2.
Pour rayonner correctement le 350 Hz, il faut une surface supérieure ou égale à 768 cm2.
La surface précédente fait 566 cm2

Les surfaces ne suivent pas tout à fait le même chemin entre les surfaces JMLC et les surfaces temporelles.
Les surfaces commencent au centre exactement au même endroit, et arrivent à peu près au même endroit puisque la longueur le long du profil du pavillon est identique au centre et au bord.
Le profil du pavillon à surfaces temporelles grandit un peu plus vite, et est un peu plus court que celui à surfaces JMLC.
Dans le chapitre sur les pavillons pour chambre de compression, le contrôle du pavillon IWATA avec des surfaces JMLC demandait une croissance plus rapide sur les dernières surfaces, ce que peuvent proposer les surfaces temporelles.
Il ne reste qu'à le vérifier réellement...Seul le pavillon à surfaces temporelles respecte la règle toute simple :
La surface est définie par les points qui sont atteint au même temps depuis la source, avec une répartition uniforme sur la surface.
Le trajet que fait l'onde réelle n'est pas l'objet de cette étude, seul le report des surfaces entre la feuille EXCEL et le plan du pavillon est étudié, nous ne voulons que connaître le bord du pavillon.
Pavillon courbe à surfaces temporelles :
J'ai simplement repris rigoureusement le même pavillon, mais en faisant en sorte que la sortie soit à 90° de l'entrée.
Un pavillon à surfaces temporelles se courbe, mais il y a un décalage angulaire entre la ligne neutre et l'angle que prennent réellement les surfaces, si nous définissons cet angle avec la droite qui relie les deux points extrêmes de la surface.
J'avais vu un décalage angulaire similaire sur un pavillon western électrique WE15A dans le livre de Jean HIRAGA sur les haut-parleurs.
La valeur indiquée était de 15° sur le plan du WE15A, il est de 27° pour la dernière surface dans mon dessin.La forme de la surface n'est pas symétrique par rapport à la ligne neutre réelle ou par rapport au milieu de la surface.
C'est un point que je n'avais jamais vu écrit, dans aucun livre, dans aucun forum.
Un bon tracé des surfaces montre certains phénomènes, certainement ressenti à l'écoute et non démontrés en pratique jusqu'à maintenant.
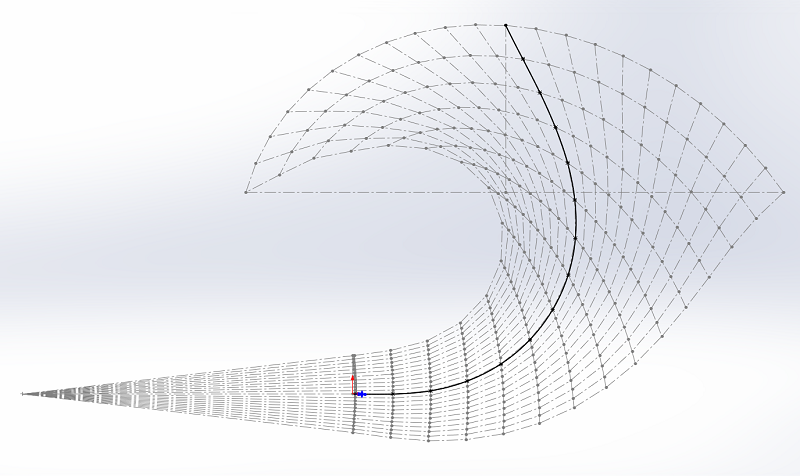
Faut-il courber un pavillon ?
Si vous pouvez vous en passer, un pavillon droit est toujours préférable.
Si vous ne pouvez pas vous en passer, limitez l'angle au maximum.
Je peux comprendre que la place manque en profondeur, j'ai plus de mal à le comprendre vers le haut ou vers le bas.
Si vous devez tout de même faire un pavillon courbe, faites-le bien, ou trouvez quelqu'un qui vous le fera bien !!!
Pavillon rectangulaire :
Un pavillon rectangulaire a une hauteur et une largeur de valeur différente, contrairement aux pavillons circulaires dont les valeurs sont identiques.
Pourtant les surfaces sont définies par les points qui sont atteint au même temps depuis la source, avec une répartition uniforme sur la surface.
Cette loi toute simple interdit que la base de la surface ne soit pas autre chose qu'une surface de révolution.
Il n'y a pas d'impossibilité pour autant, si vous tracez des surfaces de révolution plus grandes, et que vous les limitez ensuite avec une valeur différente sur la hauteur et la largeur.
Expliquons les choses en images, sur la base du pavillon IWATA.Les côtes du plan du pavillon IWATA permettent de tracer le profil du pavillon dans le plan horizontal et dans le plan vertical.
Dans le plan horizontal, j'ai ajouté les lignes d'écoulement, en allant plus loin que le profil du pavillon, la première section est carrée.
La diagonale est plus grande d'un facteur racine(2) de la hauteur et de la largeur.

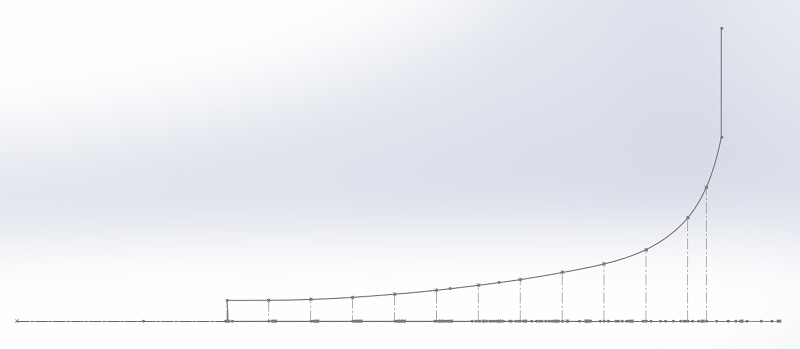
Comme pour un pavillon circulaire, il faut créer des surfaces pour pouvoir les mesurer. Je me suis limité pour l'exemple aux 9 premières surfaces, sur les 12 qui servent pour définir le côté horizontal du pavillon.

Avec le profil horizontal du pavillon, nous allons limiter les surfaces vers le haut. L'axe de révolution est à 100 mm du bord arrière du pavillon, comme sur le plan.
Puis par symétrie nous allons les limiter vers le bas.
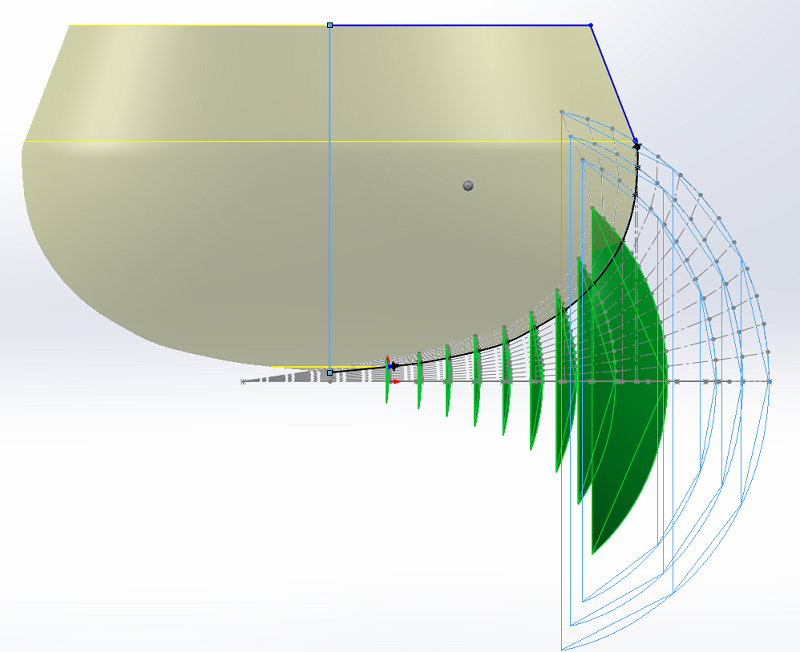
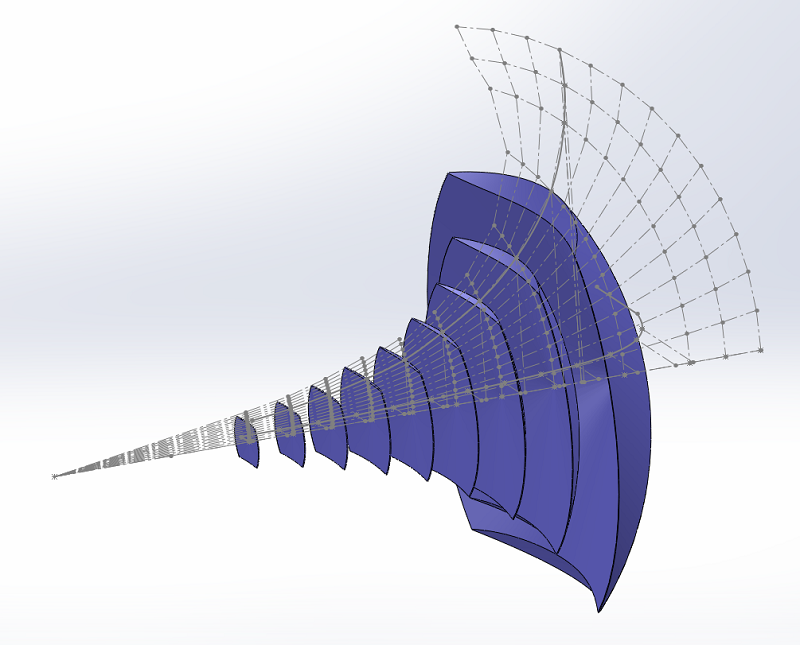
Il ne reste qu'à faire la même chose dans l'autre plan. C'est un enlèvement de matière linéaire dans ce cas, les bords sont droits.
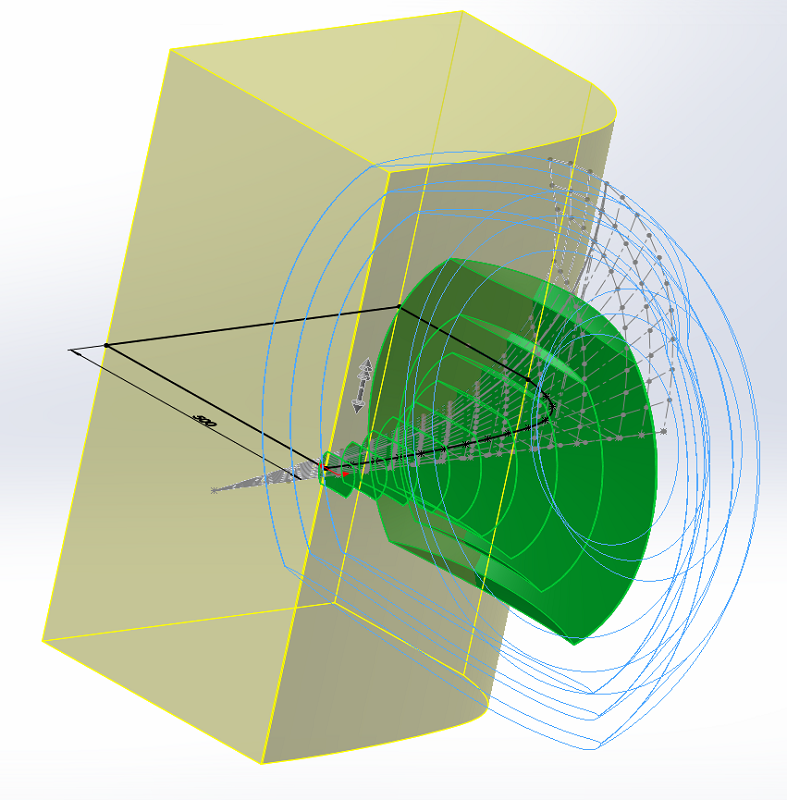
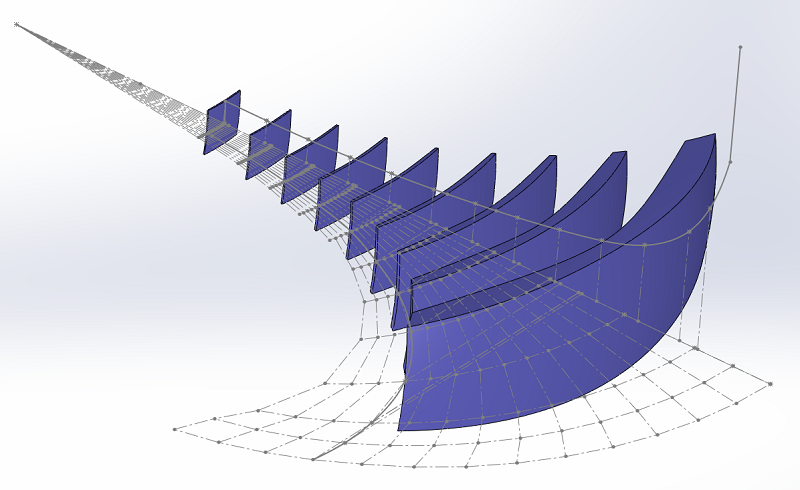
Ajoutons à notre dessin les trois dernières surfaces, et regardons le profil de la dernière surface. Surprenant, non ?
Vous pouvez lire sur les forums qu'il n'est pas possible de casser la loi d'expansion du pavillon IWATA. À ma connaissance, personne n'a tracé les surfaces comme je l'ai fait, ceci explique cela.
Le tracé d'un pavillon n'est pas une question d'équations, elles sont simples, c'est une question de dessin industriel réalisé à la CAO.
La conception en CAO est un métier, c'était mon métier parce qu'aujourd'hui je suis retraité.
Les surfaces sont le résultat des enlèvements de matière qui suivent le profil et la réalisation du pavillon avec le rayon de 100 mm. Elles n'ont rien de rectangulaire.
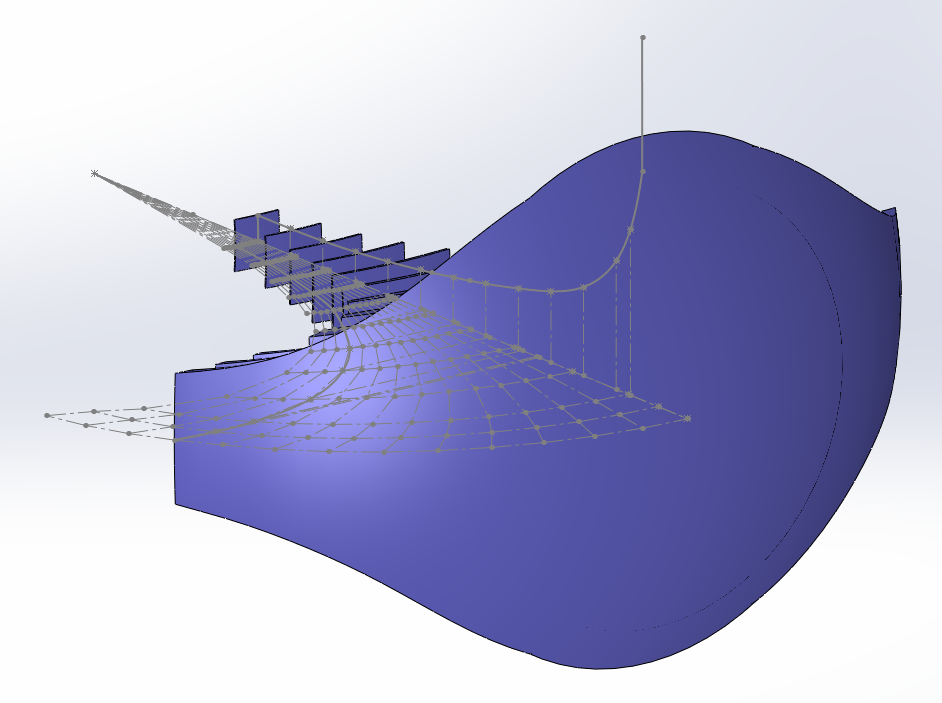
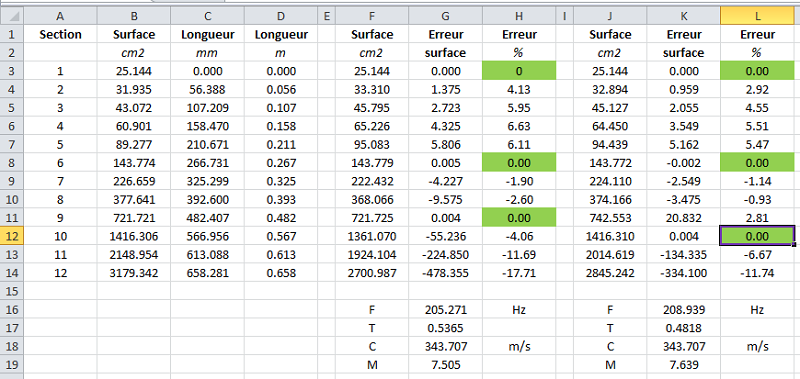
Le pavillon IWATA respecte très bien la loi d'expansion hyperbolique avec 205 < F < 210 Hz et 0.48 < T < 0.54.
Les colonnes B et C sont mesurées sur le tracé 3D, les colonnes F, G et H sont recalculés pour la vérification avec les paramètres des lignes 16, 17, 18 et 19.
Les sections 2, 3, 4 et 5 sont un problème de côtes sur le plan, problème bien visible au tracé.
Les sections 11 et 12 sont en erreur plus importante, et je n'ai pas de solution à proposer.Mon hypothèse qui dit que le tracé d'un pavillon n'est pas dans une loi d'expansion exotique et inconnue, mais dans un report des surfaces avec les points qui sont atteint en même temps depuis la source, avec une répartition uniforme sur la surface est confirmé.
Il faudra sans doute beaucoup de temps pour le faire admettre auprès d'un certain nombre d'audiophiles, qui en sont encore à refaire des pavillons étudiés dans les années 60.
Si vous lisez dans un livre que le plan du pavillon proposé utilise un T variable en fonction de la position de la surface dans le pavillon, méfiez-vous et ne réalisez pas ce pavillon.Cette étude est libre de droit, vous pouvez l'utiliser sans problème que vous soyez amateur ou professionnel.
Je ne demande qu'une chose, d'être cité explicitement.
Dominique PETOIN.
Un grand merci pour votre visite. --- Retour direct en haut de la page ---

Un grand-père facétieux disait à ses petits enfants que le grand truc blanc tout en haut du Puy-de-Dôme était un thermomètre géant.
Quand il deviendra tout rouge il faudra vite se sauver, parce que le volcan va se réveiller !!!
Dôme Acoustique
Contrôle de validation W3C du code HTML 5 de la page, copiez l'adresse de la page avant de cliquer sur le lien.
Contrôle de validation W3C des CSS de la page, copiez l'adresse de la page avant de cliquer sur le lien.
Test "responsive" en simulant des écrans de smartphone de résolution différentes.
Ce sont trois outils de contrôle pour le webmaster du site Dôme Acoustique, c'est inutile pour les utilisateurs.
Avoir le lien dans chaque page est plus simple pour les retrouver.