Page affichée à 14:42:59
vendredi 26 avril 2024
Ce site n'utilise pas de cookie.Dôme acoustique Compteur pour tout le site : 14 047 033
Nombre actuel de lecteurs : 108.Faire
un don
par
PayPalLe site de Dominique, un amateur passionné
2-3-2-2 : Les pavillons pour chambre de compression
Mise à jour : 14 septembre 2023, Antimode 11.
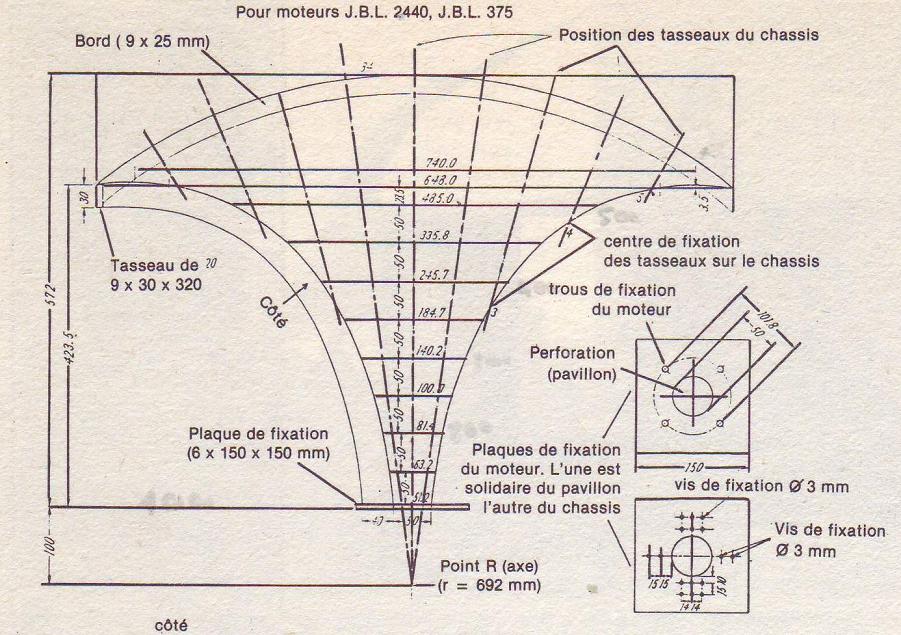
Pavillon IWATA :
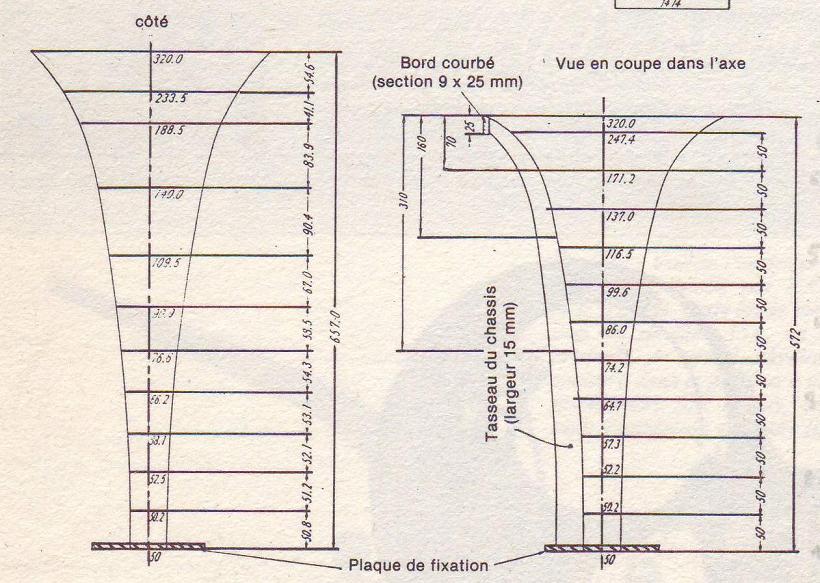
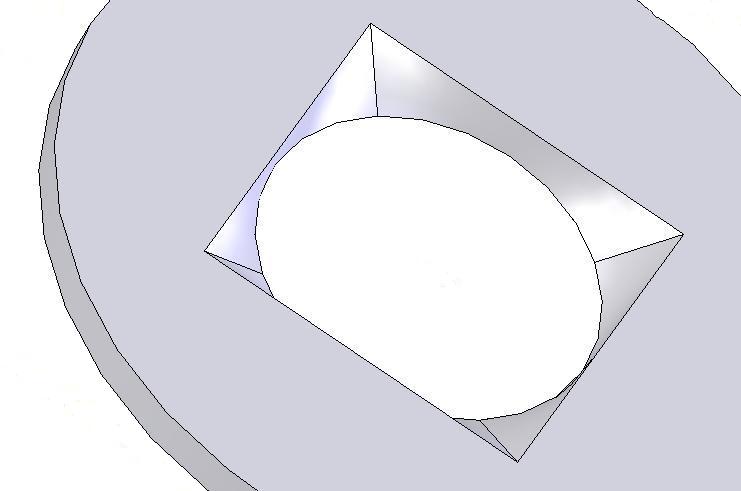
Le dessin en 3D est le tracé exact du pavillon dont le plan est ci-dessus.
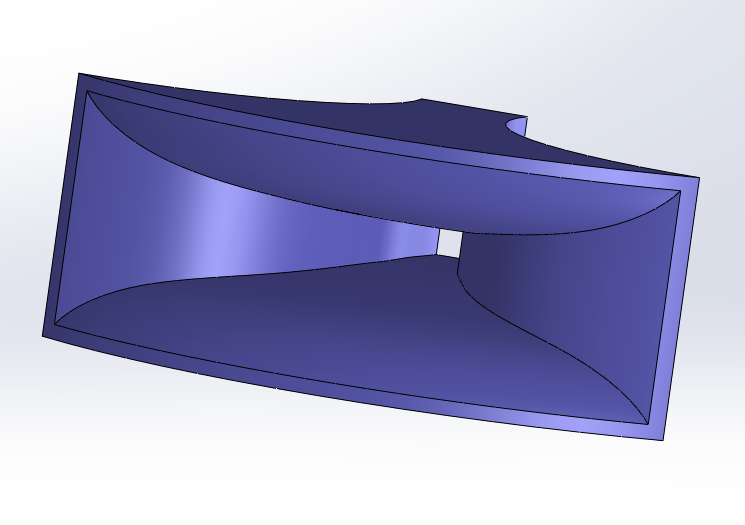
Quelle est la loi d'expansion du pavillon IWATA ?
Pour pouvoir calculer des pavillons qui ressemblent au pavillon IWATA, il faut trouver la loi d'expansion et les règles de calculs.
Sur les forums j'ai lu que ceux qui avaient essayé n'y étaient pas arrivés...
Je vous invite à prendre connaissance du chapitre sur Le report des surfaces pour avoir les explications sur les surfaces temporelles.
Dans ce chapitre, je ne garde plus que deux types de surfaces, JMLC et temporelle.
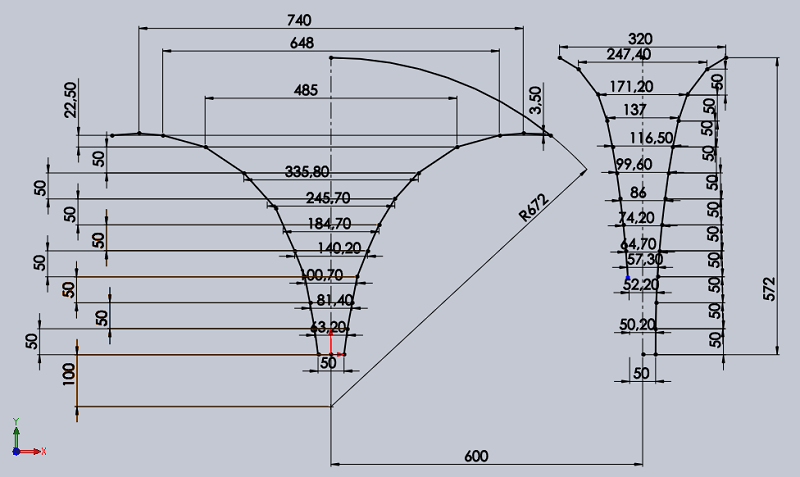
Les autres surfaces sont sans intérêt, et obligent à faire une gymnastique avec le coefficient T et la fréquence de calcul F. La surface temporelle va directement au résultat.La première chose à faire est de refaire un tracé du pavillon pour pouvoir mesurer les côtes dont nous avons besoin.
Il y a un gros piège dans le plan fourni, il n'y a pas de correspondance entre les dimensions dans les deux vues du plan.
Le tracé a déjoué ce piège, d'autres sont sans doute tombés dedans.
Les côtes manquantes ont été mesurées, une bonne CAO, et le savoir l'utiliser, aident bien pour cela.!
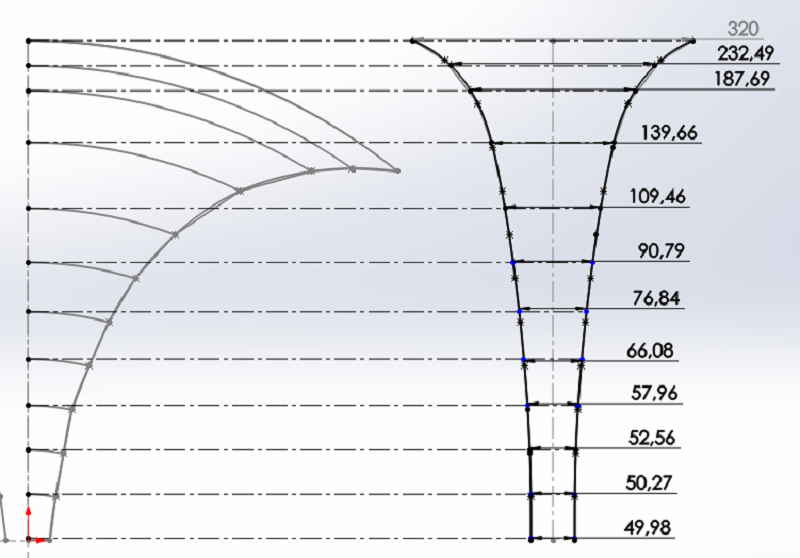
Le pavillon IWATA avec l'hypothèse des surfaces JMLC respecte à peu près la loi d'expansion hyperbolique avec F = 224 Hz et T = 0.42, ce qui me semble une valeur trop faible pour le T.
Les deux paramètres, F et T, permet d'annuler les erreurs sur trois surfaces.
Les erreurs sont assez importantes entre les points d'annulation.
Hypothèse de surface JMLC :
La méthode JMLC est expliquée par son auteur dans le chapitre des Pavillon HYPEX.
Les deux dernières sections, celles qui sont très souvent en erreur, ne sont pas définies par le profil du pavillon dont les limites sont en bleu.
Dans le plan vertical, j'ai prolongé arbitrairement le profil pour pouvoir accrocher la section.Pour limiter les erreurs en début de pavillon, il faut augmenter T vers 1.00.
Pour limiter les erreurs en fin de pavillon, il faut diminuer T vers 0.00.
Aucune solution ne permet de ne plus avoir d'erreur.
Je préfère travailler sur la légère correction du plan initial et garder des paramètres de calculs constants.
L'idée d'un T variable avec la longueur vient du livre de Francis IBRE, bien entendu itinéraire d'un Audiophile, son pavillon n'utilise pas la meilleure forme d'onde.
Hypothèse de surface temporelle :
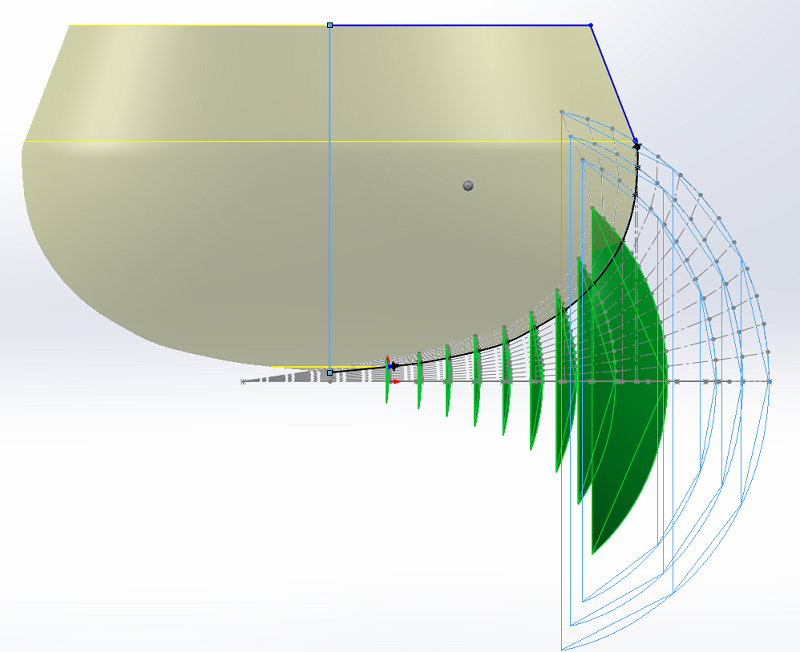
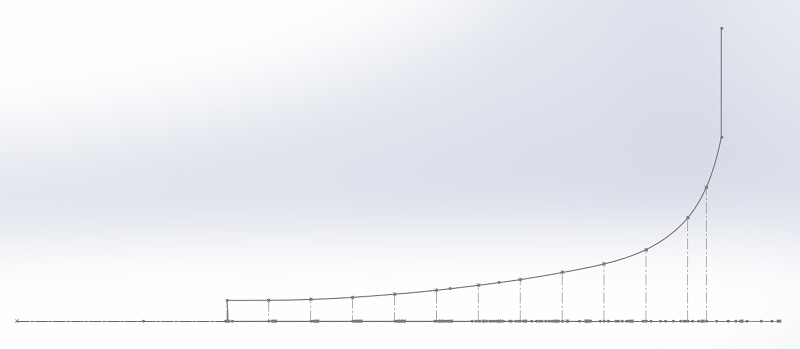
Les côtes du plan du pavillon IWATA permettent de tracer le profil du pavillon dans le plan horizontal et dans le plan vertical.
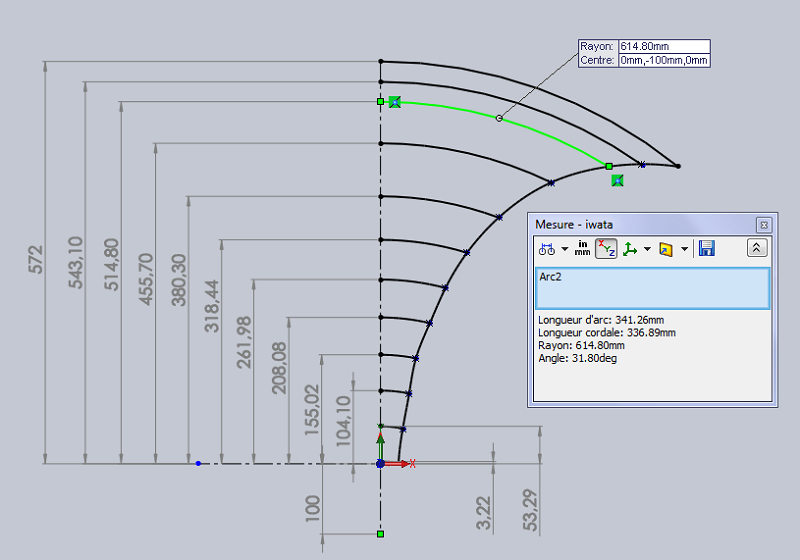
Dans le plan horizontal, j'ai ajouté les lignes d'écoulement, en allant plus loin que le profil du pavillon :
La première section est carrée, la diagonale est plus grande d'un facteur racine(2) de la hauteur et de la largeur.
Il faut créer des surfaces pour pouvoir les mesurer.
Je me suis limité pour l'exemple aux 9 premières surfaces, sur les 12 qui servent pour définir le côté horizontal du pavillon.
Les surfaces ne peuvent être que circulaires au départ, elles seront limitées ensuite.
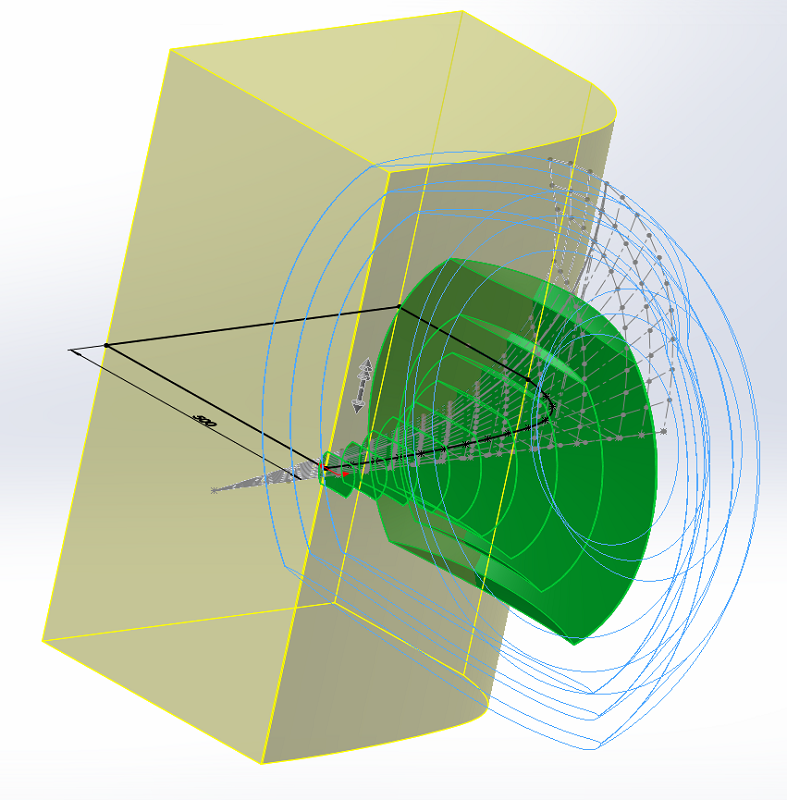
Avec le profil horizontal du pavillon, nous allons limiter les surfaces vers le haut. L'axe de révolution est à 100 mm du bord arrière du pavillon, comme sur le plan.
Puis par symétrie nous allons les limiter vers le bas.
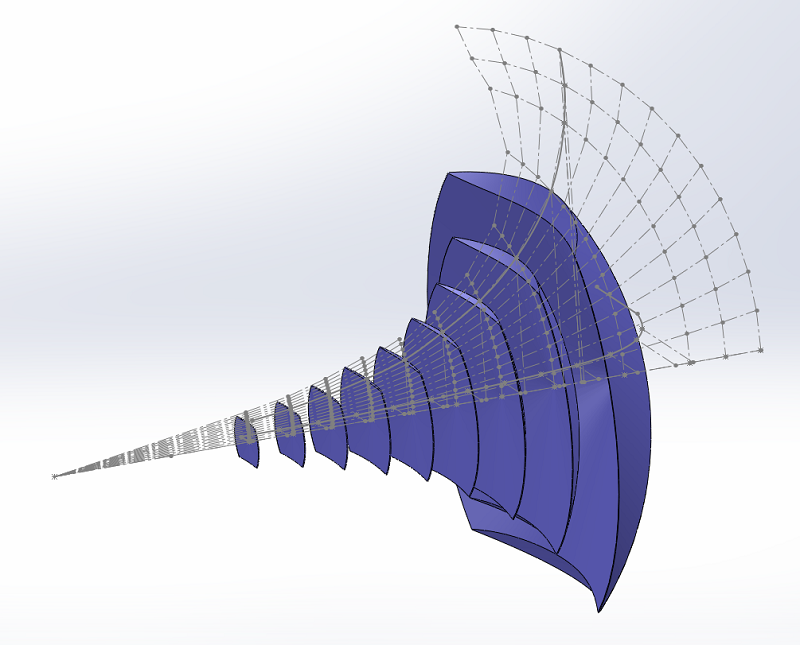
Il ne reste qu'à faire la même chose dans l'autre plan, c'est un enlèvement de matière linéaire dans ce cas, parce que les bords sont droits.
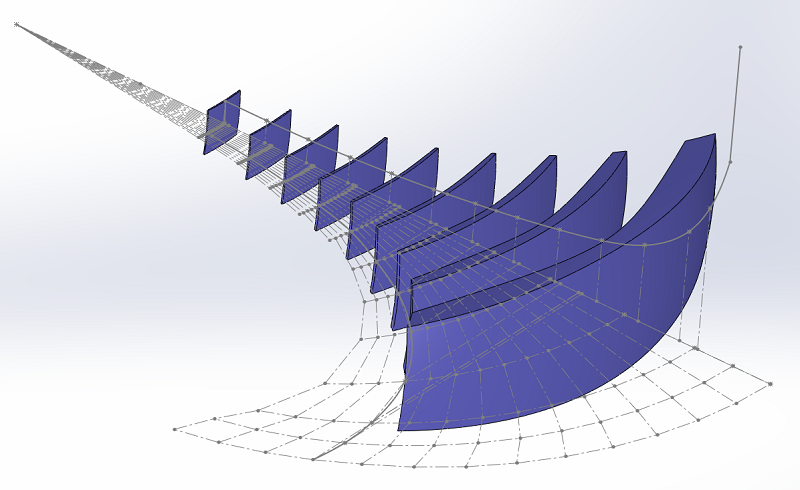
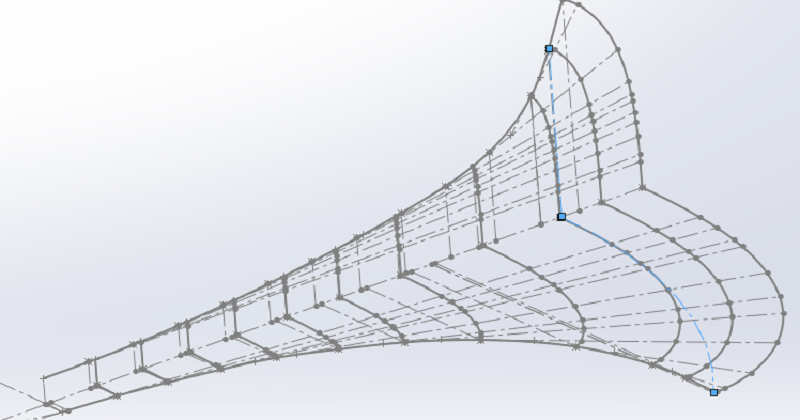
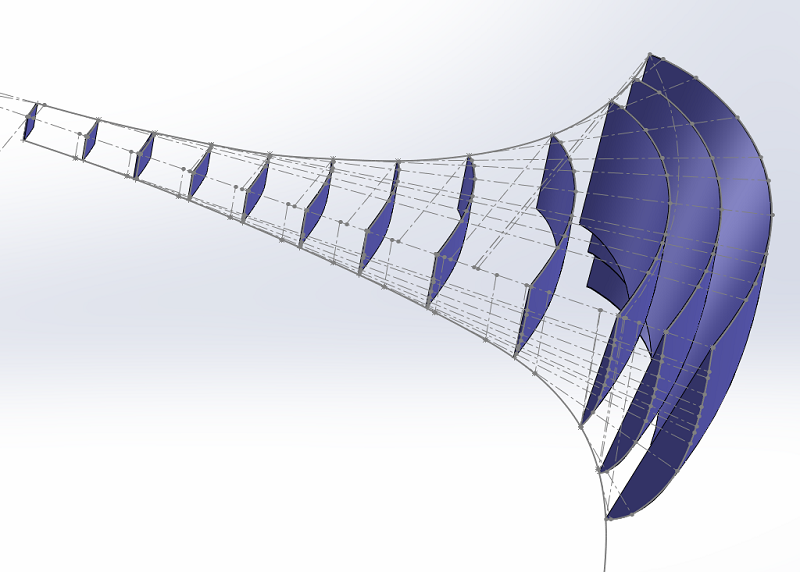
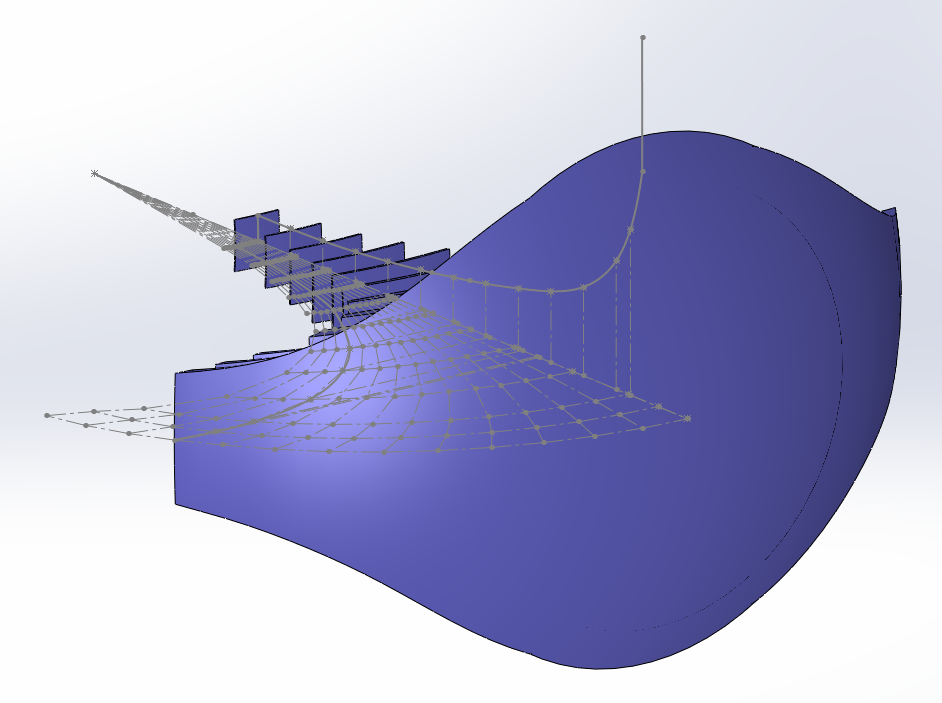
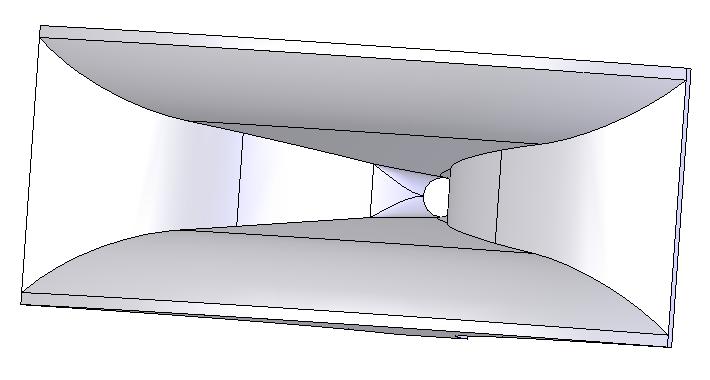
Ajoutons à notre dessin les trois dernières surfaces, et regardons le profil de la dernière surface.
Surprenant, non ?
Vous pouvez lire sur les forums qu'il n'est pas possible de casser la loi d'expansion du pavillon IWATA, à ma connaissance, personne n'a tracé les surfaces comme je l'ai fait, ceci explique cela.
Le tracé d'un pavillon n'est pas une question d'équations, elles sont relativement simples, c'est une question de dessin industriel réalisé à la CAO, c'est un métier, c'est mon métier.
Les surfaces sont le résultat des enlèvements de matière qui suivent le profil et la réalisation du pavillon avec le rayon de 100 mm. Elles n'ont rien de rectangulaire.
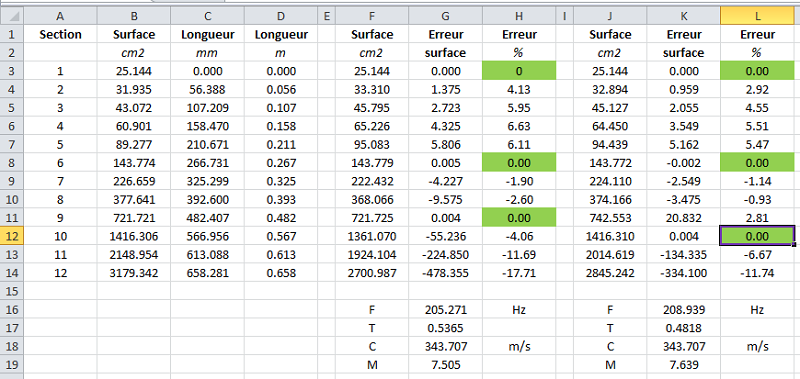
Le pavillon IWATA avec l'hypothèse des surfaces temporelles respecte bien la loi d'expansion hyperbolique avec 205 < F < 210 Hz et 0.48 < T < 0.54.
Les deux paramètres F et T permets d'annuler les erreurs sur trois surfaces.
Un T de 0.54 est plus faible que l'idéal T = 0.707, mais reste encore réaliste.
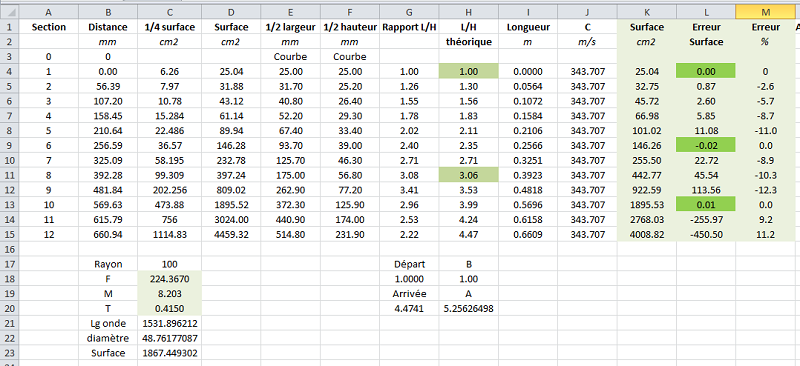
Les colonnes B et C sont mesurées sur le tracé 3D, les colonnes F, G et H sont recalculés pour la vérification avec les paramètres des lignes 16, 17, 18 et 19.
Les sections 2, 3, 4 et 5 sont un problème de côtes sur le plan, problème bien visible au tracé.
Les sections 11 et 12 sont en erreur plus importante, et je n'ai pas de solution à proposer.Comparer avec l'hypothèse des surfaces JMLC, les erreurs sont plus faibles entre les trois surfaces d'annulation, surtout pour les sections 7, 8 et 9, et aussi importantes sur les deux dernières surfaces.
Les différences ne sont pas significatives sur les premières sections, mais au niveau des plus grandes sections les surfaces temporelles creusent l'écart.
Conclusions :
À partir du même plan du pavillon, en fonction des hypothèses retenues sur le report des surfaces, nous pouvons retrouver, ou ne pas retrouver, la loi d'expansion initiale.
À partir d'une loi d'expansion, en fonction des hypothèses retenues sur le report des surfaces, vous n'aurez pas le même tracé du pavillon, ni le même rendu sonore.
Je n'ai pas encore approfondi dans le détail les calculs faits par JMLC (Jean-Michel Le CLEAC'H) pour les plans de pavillons qu'il proposait.
Les surfaces JMLC sont réputées à l'écoute, les surfaces temporelles vont apporter un petit quelque chose en plus.
Faire un pavillon "genre IWATA" adapté à notre besoin :
La loi d'expansion est hyperbolique avec T = 0.50 environ, le calcul n'est un secret pour personne.
Le calcul avec des ondes elliptiques dans le plan vertical correspond bien au pavillon IWATA dont nous avons les plans, il n'y a rien à inventer de ce côté.
Je pense qu'il faudrait aussi des ondes elliptiques dans le plan horizontal, ce n'est pas le plus facile à tracer.
Le rapport largeur / hauteur est bien respecté sur presque toute la longueur, il sera repris.
Margré tout, ce ne sera pas simple de passer de la loi d'expansion au plan de réalisation d'un pavillon...Le raccordement entre la compression et le pavillon a toujours été le point faible de ces associations.
Le rapport L/H des compressions est de 1.00, ce qui est normal puisqu'elles sont circulaires.
Le pavillon commence avec un rapport L/H de 1.00 pour un bon raccordement, pourtant un point ne va pas.
Si vous tracez le rapport L/H de la compression jusqu'à l'extrémité du pavillon, il y a un accident dans la progression, et l'acoustique a horreur des accidents.Vous allez me dire "Mais c'est ben sur !!!" parce que je viens de mettre le doigt sur LE problème.
Mais si c'est aussi évident que cela, pourquoi personne n'en tient compte ?
Pourquoi trouvons-nous un grand n'importe quoi sur les réalisations commerciales ?
Je ne ferai pas de compromis sur ce point comme le prouvent les tracés ci-dessous.
Les 90 mm ont été choisis pour faire la zone de raccordement avec 5 planches de CTP de 18 mm. C'est dans cette zone que nous passerons d'une surface ronde à une surface rectangulaire.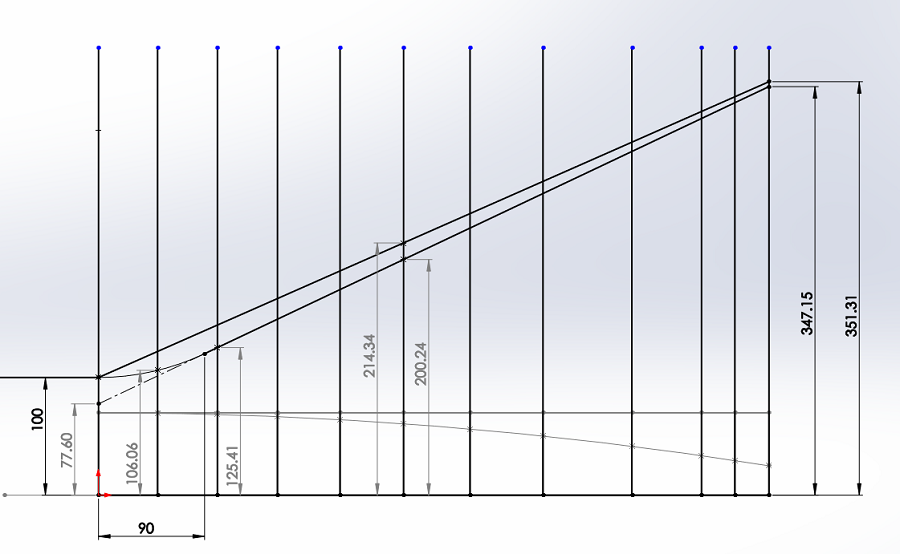
Raccordement compression / pavillon :
Vous pouvez faire la meilleure réalisation du monde, avec le meilleur profil d'expansion qui soit, si vous raccordez une compression dont la sortie est ronde à un pavillon dont la gorge est carrée, vous allez avoir un mauvais résultat global.
La raison est simple, dans les 4 angles du carré de la gorge, il n'y a pas une continuité de profil avec la compression.
Pour raccorder une compression de 1" :
Le pavillon qui est représenté à une entrée de 50x50 mm.
Si vous devez raccorder une compression de 1", 25.4 mm de sortie théorique, il existe des adaptateurs rond / carré plus ou moins long.
Si vous mesurez le cône de sortie du moteur de votre compression, vous pouvez déterminer la longueur de l'adaptateur pour limiter les accidents de raccordement des profils au moins sur le plan horizontal et vertical.
Si vous devez faire réaliser un adaptateur sur plan, et que vous voulez une sortie bien carrée sans rayons dans les angles, c'est un usinage par électroérosion au fil de la partie interne que sera nécessaire, et vous allez sentir passer l'addition...
Pour raccorder une compression de 2" :
Si vous devez raccorder une compression 2", il n'y a pas d'adaptateur possible.
J'ai eu une question pour une compression qui faisait 49 mm de diamètre, et dont l'adaptateur devait faire 5.9 mm de long.
Dans le plan horizontal et vertical, le raccordement entre le diamètre de 49 mm et le carré du pavillon de 50 mm est presque parfait.
Par contre dans les angles l'accident de raccordement reste très important.Avec un adaptateur conique diamètre 49 et 50 mm, épaisseur 6 mm.
L'accident dans la variation des sections est parfaitement visible, en 0 mm, la surface passe de 19.63 cm2 à 25 cm2.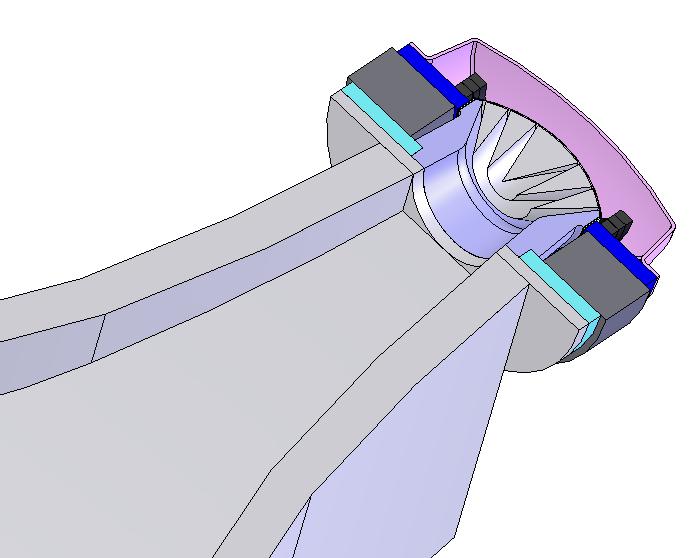
Avec un adaptateur rond D=49 mm, carré 50 mm épaisseur 6 mm.
En 6 mm, la surface passe de 18.86 cm2 à 25 cm2, une variation très importante et sans relation avec la progression de la compression juste avant, et celle du pavillon juste après.
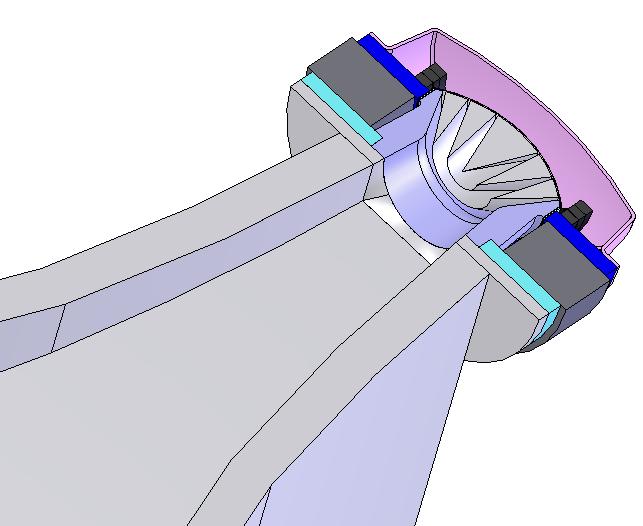
La meilleure solution est de continuer avec un rayon de 25 mm de la gorge du pavillon jusqu'à la bouche.
Le raccordement est parfait au niveau de la gorge avec une compression dont la sortie fait un diamètre de 50 mm.
Pour une compression dont le diamètre est 49 mm, un simple adaptateur conique suffit, ce n'est pas cher même en métal.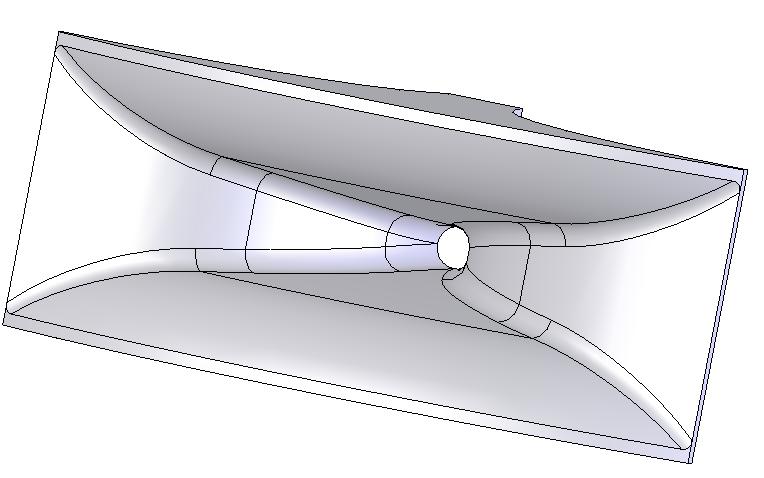
J'ai le sentiment que cette solution ne va pas vous plaire, personne ne l'a jamais réalisée jusqu'à maintenant.
Par contre ce qui se fait le plus souvent est de passer d'un rayon de 25 mm à un rayon nul sur une partie de la longueur du pavillon.
C'est la solution proposée par la revue l'Audiophile pour la modification des pavillons ALTEC 515.
Au tracé, le compromis n'est pas si mal que ça, mais un puriste y trouvera à redire :
Quelles sont les sections réelles au début du pavillon ?
Que devient la loi d'expansion ?
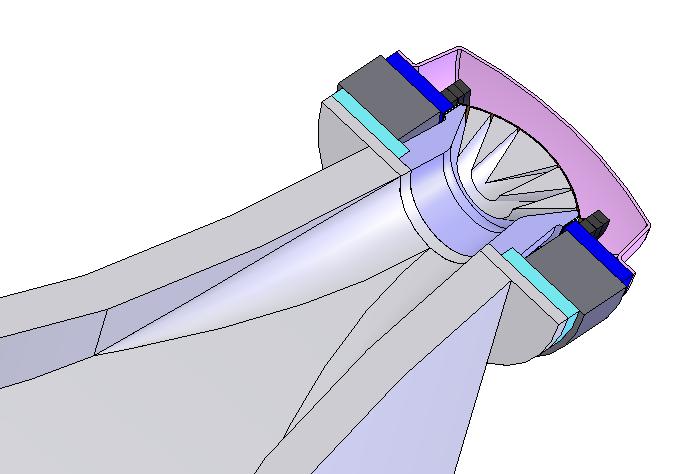
Un peu de calculs :
Les dessins ci-dessus montrent s'il y a visuellement un problème, ou si le raccord semble bon.
L'étape qui vient consiste à passer d'un "raccord qui semble bon" au "respect de la loi d'expansion" en intégrant la compression.
Ce ne sera pas possible dans tous les cas, mais les erreurs sur la loi d'expansion seront limitées.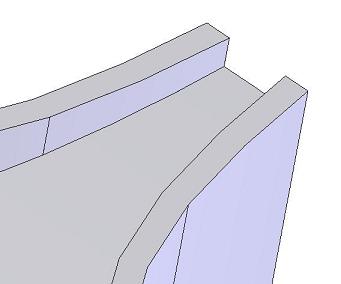
Notre pavillon a une section de gorge, de début de 50x50 mm = 25.00 cm2
À une distance de 156 mm = 0.156 m, la section est de 67.2x100 mm = 67.20 cm2
Je fais l'hypothèse que les ondes sont planes, ce n'est pas une grosse erreur en début de pavillon.
Enfin, la compression à un diamètre de sortie de 49 mm, c'est-à-dire une surface de 18.86 cm2.Coefficient d'expansion : M = 1 / X * LOG( S / Sg ) = 2.7528
Avec X = 0.156 m, S = 67.2 cm2 et Sg = 25 cm2.Longueur de la liaison : X = 1 / M * LOG ( Sg / Scomp ) = 0.044 = 44 mm
Avec M = 2.7528, Sg = 25 cm2, Scomp = 18.86 cm2.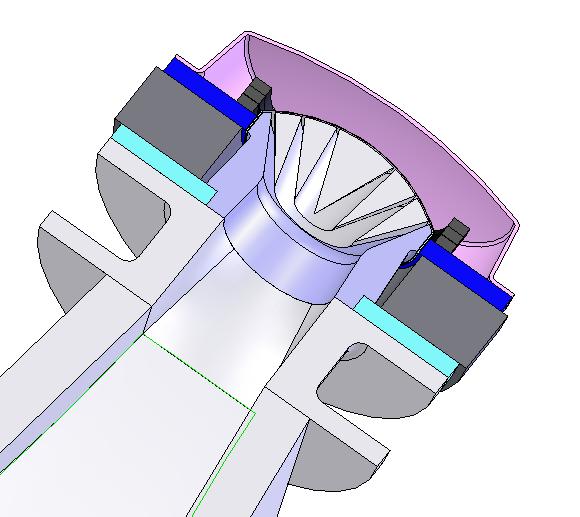
Le raccordement est très satisfaisant sur le plan théorique.
C'est au moment de faire réaliser l'adaptateur rond / carré que vous allez comprendre combien c'est cher la découpe au fil...
La solution est de garder un rayon de 5 mm au niveau du carré de la pièce d'adaptation, et de compléter le rayon avec du mastic dans le pavillon.
L'adaptateur peut être fraisé ou moulé sans difficulté.
Le rayon dans le pavillon ci-dessous va trop loin, il fait le faire plus court.
De rayon 25 à 5 mm en 44 mm ==> 11 mm de rayon dans le pavillon, et pas plus...
44 / (25 - 5) * 25 = 55 mm. 55 - 44 = 11 mm.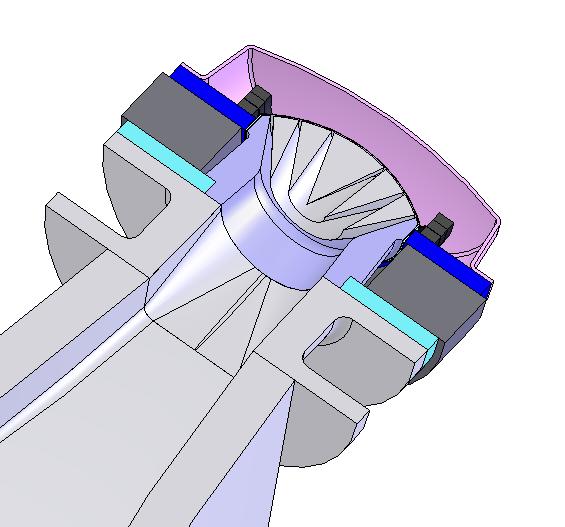
En conclusion :
Pour obtenir un raccordement parfait entre une compression et un pavillon, il faut deux conditions :
- Que le pavillon soit rond.
- Que le pavillon soit calculé à partir de la compression, et pour une compression bien définie.
Il est possible d'obtenir quelque chose de tout à fait acceptable avec un pavillon dont la gorge est carrée, à condition de faire un minimum de calculs, et de se souvenir que la progression des surfaces est plus importante que la continuité des lignes dans les plans de coupe horizontale et verticale.
Le pavillon WE15A :
Adaptation à votre chambre de compression :
Le calcul ci-dessous apporte une solution numérique au chapitre de l'audiophile sur : Le dressage des escargots.
Une bonne théorie n'a d'intérêt qu'à partir du moment ou elle est facile à calculer.
Je ne traite que le raccordement du pavillon à la chambre de compression, dans le cadre d'une loi d'expansion hyperbolique avec T compris entre 1 et 0.
À ma connaissance c'est une exclusivité, aussi la méthode de calculs par itération ne sera pas expliquée.
Sachez simplement que j'ai pas mal galéré pour y arriver.Pour respecter parfaitement la continuité du profil entre la compression et le pavillon, il n'est pas possible de réaliser un pavillon pour une compression donnée sans mesurer les dimensions internes de la compression.
C'est l'idée qui est sous-jacente à ce calcul, à une compression correspond un début de pavillon et un seul.Je voudrais préciser un peu plus le terme "Début de pavillon" :
La loi d'expansion sera donnée par le calcul ci-dessous, et je pense que vous garderez cette loi sur toute la longueur du pavillon.
Le début du pavillon passe d'une section ronde à une section carrée ou rectangulaire, pour une même loi d'expansion, il y aura la même surface, mais pas forcément la même forme.
Ensuite plus nous allons avancer vers la bouche du pavillon, plus la forme sera différente, sans que la surface change pour la même distance.
Suivant que vous retenez une hypothèse d'onde plane, cylindrique, sphérique, ellipsoïdique, vous n'allez pas avoir le même pavillon au final.
Nous allons avoir, pour une même compression et une même loi d'expansion, une influence à l'écoute par la simple différence de forme et de directivité du pavillon.
La première opération consiste à enlever la grille de protection de la compression.
Derrière cette grille se trouve une sorte de cône qui va jusqu'à la pièce de mise en phase.
C'est cette partie plus ou moins conique qu'il faut mesurer.Sans utiliser d'instrument de mesure compliqué, un pied à coulisse qui fait aussi pied de profondeur et quelques pièces de monnaie permettent de faire les mesures avec un minimum d'erreur.
Diamètre des pièces de monnaie
Dans les magasins de bricolage, un pied à coulisse au 1/10 de millimètre est à 12 € environ.
Le rayon du bord de la pièce est considéré comme un angle vif.
Ce n'est pas vrai en pratique, mais l'erreur est faible.
Un tableau de correction vous dira la correction à apporter aux longueurs mesurées en fonction du rayon de la pièce utilisée.Pour chaque pièce utilisée, il faut mesurer le diamètre, l'épaisseur de la pièce, glisser la pièce dans le cône de la compression sans forcer, et mesurer la distance de la face supérieure de la pièce à la face supérieure de la compression.
Les valeurs proposées par défaut sont celles de la compression RCF N482 de 1" de sortie. Ce n'est pas récent !!!Le calculateur ci-dessous vous trouvera en un temps record, et avec un sérieux paquet d'itérations sur F et T, les valeurs à utiliser pour le calcul de votre pavillon.
La loi d'expansion est de la forme : S = So * ( ( COSH( M * L / 2 ) + T * SINH( M * L / 2 ) )2 )
avec
M = 4 * Pi * F / C.
C'est une loi d'expansion hyperbolique, la seule qui passe par 3 points spécifiés, la solution est unique.
Valeurs utilisées pour le calculs Surface de calcul en cm2 5.067 3.767 2.956 Longueur de calcul en m 0.0000 0.0081 0.0170
Valeurs obtenues avec F = 1558.45 Hz, M = 56.9791 m-1, T = 0.7067 et C = 343.707 m/s en 35191 itérations. Surfaces calculées en cm2 5.067 3.767 2.956
J'ai une compression existante, et je veux faire un pavillon qui coupe plus bas :
Il faut trouver un profil de raccordement qui respecte la tangente avec la compression d'un côté, avec le pavillon de l'autre.
Le profil le plus simple est un cône.
Un profil avec une équation du 2e ordre sera plus précis, mais il faut trouver les coefficients qui vont bien en tâtonnant beaucoup.
Pavillon pour compression RCF N482 :
J'ai utilisé la méthode ci-dessus, avec à l'époque une simple calculette, et je ne me suis trompé pas dans les calculs.
Avec l'outil proposé aujourd'hui, cela ne vous arrivera pas...
Mon pavillon était réalisé avec M = 36 et T = 0.707.Vue en coupe du cône de sortie de la compression et du pavillon.
Les ondes sont supposée plane, ce qui n'est pas vrai en pratique.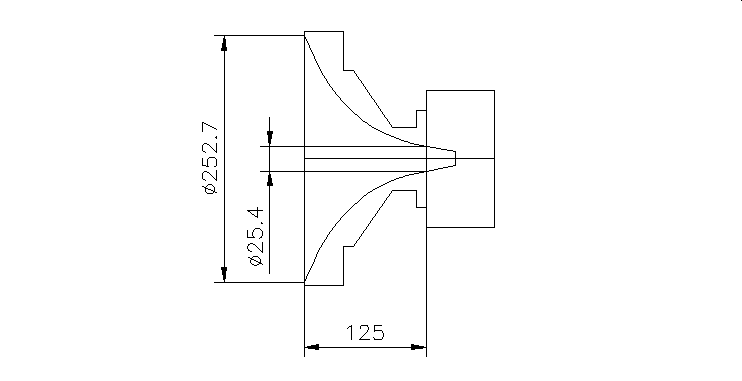
La même compression et le même pavillon, mais avec des surfaces JMLC.
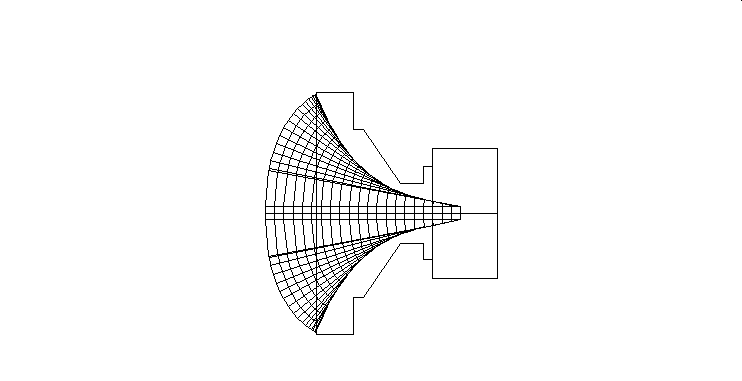
Jean Michel LE CLEAC'H, aujourd'hui décédé, proposait une méthode de calcul avec une forme d'onde plus proche de l'ellipse que de la sphère.
Ce profil présente la particularité de passer à la verticale à 90°, et de revenir à l'arrière à 180° et même plus.
Je considère ce profil comme idéal, j'en ai discuté avec lui sur un forum.
La méthode a aussi été publiée dans Musique & Technique no6La réalisation d'un pavillon sphérique n'est pas facile sans tour à bois. Mais avec un peu de méthode, il est possible de s'en passer.
Voici deux liens, Réalisation d'un pavillon et Réalisation d'une ogive.
Photos du pavillon :
Vue de dessus, la compression est sans grille, les surfaces et tangentes sont respectées.

Vue de côté, j'aurai préféré des sections plus massives, mais il aurait fallu une plaque démontable pour la fixation de la compression sur le pavillon.

Compression RCF N482.

Le grave est un 38 cm, le large bande un 21 cm, le pavillon est posé au sol.
Le baffle plan est une ancienne version Tweeter FOSTEX T925 et large bande SIARE ALNICO.
La suite à donner à ce chapitre :
La chambre de compression est restée longtemps dans un placard, c'est le pourquoi de ce chapitre non terminé.
Le passage en triamplification active va me faire ressortir cette compression + pavillon du placard.
J'ai essayé une coupure basse, vers 1500 Hz, sans résultats convaincants, la coupure à 8000 Hz reste la meilleure.
Un simple tweeter suffit.
Nous avons simplement mis en évidence la cohérence de la restitution d'un haut-parleur large bande, et aujourd'hui je l'essayerai sans tweeter.Dans un autre domaine, certain d'entre-vous utilise un système a deux voies avec grave + compression + pavillon + filtre passif.
J'ai utilisé cette solution avec un grave de 38 cm en bass-reflex, la compression N482 avec son pavillon décrit ci-dessus, et le filtre ci dessous :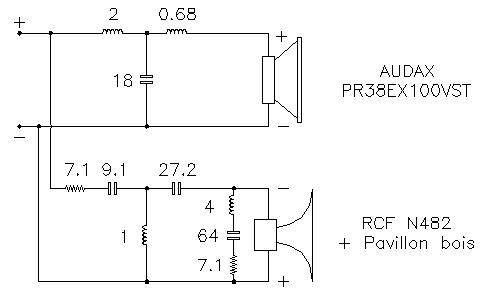
Aujourd'hui, dans les mêmes conditions j'utiliserai le même filtre, sauf l'atténuateur qui passerait à impédance constante, et qui serai placé après le condensateur de 27.2 mF.
Avec le 38 cm, il y avait un trou dans le médium, ne copiez donc pas cette solution avec les mêmes haut-parleurs.
D'autre part il ne faut pas utiliser de compression trop petite avec des graves de grand diamètre :
- Avec un 38 cm, c'est une compression de 2", et une coupure à 800 Hz maxi + un tweeter.
- Avec un grave de 30 cm, c'est une bonne compression de 1.4", et une coupure à 1250 Hz maxi.
- Avec un grave de 24 cm, c'est une compression de 1", et une coupure à 2000 Hz maxi.
Un grand merci pour votre visite. --- Retour direct en haut de la page ---

Un grand-père facétieux disait à ses petits enfants que le grand truc blanc tout en haut du Puy-de-Dôme était un thermomètre géant : Quand il deviendra tout rouge il faudra vite se sauver, parce que le volcan va se réveiller !!!
Dôme Acoustique
Contrôle de validation W3C du code HTML 5 de la page, copiez l'adresse de la page avant de cliquer sur le lien.
Contrôle de validation W3C des CSS de la page, copiez l'adresse de la page avant de cliquer sur le lien.
Ce sont deux outils de contrôle pour le webmaster du site Dôme Acoustique, c'est inutile pour les utilisateurs.
Avoir le lien dans chaque page est plus simple pour les retrouver.