Page affichée à 08:01:56
mardi 23 avril 2024

Ce site n'utilise pas de cookie.		 logo7 Dôme acoustique Compteur pour tout le site : 14 006 945

Nombre actuel de lecteurs : 32.		 Faire
un don
par
PayPal
Le site de Dominique, un amateur passionné

 

1-3-3-7 : Les effets du sol pendant la mesure

Mise à jour : 14 juin 2023, Antimode 11.

 

Remarque préliminaire :

Pour couper court à toute polémique, je n'ai rien inventé.
Je ne fais que vous proposer un outil de calcul à partir d'une méthode décrite dans le livre de Joe D'Appolito, Le haut-parleur : Manipulations et mesures électroacoustiques, page 82.
L'outil de calcul vous sera d'une bonne aide, je n'en doute pas une seconde.
Les deux liens ci-dessous disent la même chose que ce chapitre a des petites nuances près.

La fin du chapitre propose une solution, en ajoutant une mesure à 2 cm du cache noyau du HP de graves, et en fusionnant cette deuxième mesure à la première effectuée de plus loin.
Le résultat est une courbe de réponse parfaitement exploitable du grave à l'aigu pour une correction par convolution dans rePhase par exemple.
Là encore je n'ai rien inventé, la méthode est décrite dans le livre de Joe d'Appolito.

 

Je lie ce chapitre à celui sur l'influence du local sur les enceintes acoustiques, la méthode de calcul se ressemble beaucoup dans les deux cas.
Cette "liaison" n'est pas évidente en première approche, je vais faire en sorte qu'elle le devienne...

 

Réflexion sur le sol :

C'est un cas qui nous arrive à tous.
Vous mesurez en champ lointain (3 à 4 fois le diamètre du HP) ou au point d'écoute, et vous avez un trou dans la courbe de réponse dans le grave.
Pourquoi ce trou ?
Parce que le micro commence à capter le signal direct qui vient du HP, puis il capte la réflexion de ce signal qui a été réfléchi par le sol.
Ce signal réfléchi peut arriver en phase, en opposition de phase, en quadrature de phase, ainsi que toutes les autres valeurs en fonction de la longueur de chacun des trajets et de la fréquence du signal : c'est en théorie une réponse en peigne.

Pourtant, vous n'avez commis aucune erreur dans votre méthode.
Vous avez mis le micro ou vous le souhaitiez, vous avez lancé la mesure.
Mais les ondes sonores vous jouent un mauvais tour avec cette réflexion sur le sol, mais aussi sur les murs et le plafond.
Nous allons donc calculer, à partir de la distance, de la hauteur du haut-parleur et de la hauteur du micro, à quelle fréquence il y a un trou dans la courbe de réponse, pour ne pas en tenir compte lors de la lecture du résultat sur la courbe de réponse.

Il y a un moyen très simple de vérifier que le trou dans la courbe de réponse est bien à cause de la réflexion sur le sol, la mesure en champ proche, avec le micro à 0.11*D, ou D est le diamètre de la membrane.
Si en champs proche il n'y a pas de trou, et qu'il existe en champ lointain ou au point d'écoute, c'est bien la distance de mesure qui est la cause.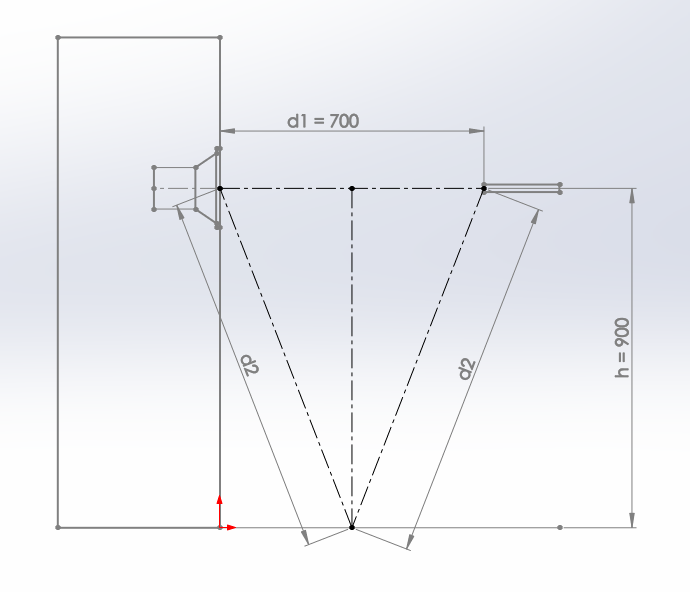

Hauteur micro différente de la hauteur HP

 

Aux très basses fréquences, le micro capte deux signaux de plus en plus en phase au fur et à mesure que la fréquence baisse :

  • Le signal qui vient directement du haut-parleur.
  • Le signal qui part du haut-parleur, qui se réfléchit sur le sol, et qui revient au micro.

Deux signaux en phase, c'est +6 dB aux très basses fréquences.
Il faut tenir compte que le signal réfléchi sur le sol parcourt une distance plus grande que le signal direct, avec une atténuation de 6 dB à chaque fois que la distance double.

Dans le dessin ci-dessus, j'ai mis le micro à la même hauteur que le HP de grave, ce qui est le cas le moins fréquent, et aussi le plus simple à calculer.
Les outils de calculs sont avec une hauteur différente entre le HP et le micro, que le micro soit au-dessus ou au-dessous du HP.

 

Un point important :

Si vous imaginez le micro au point d'écoute, que la mesure vous montre un trou dans la réponse entre 50 et 200 Hz, quand ce sont vos oreilles qui sont à la place du micro, vous avez aussi le trou dans la réponse.
Ce trou est créé par les deux signaux, l'un direct et l'autre réfléchi par le sol, il ne peut pas se corriger simplement...
Le micro capte bien la même chose que vos oreilles...

 

Prenons un exemple :

Le dessin ci-dessous est à l'échelle avec des côtes, les valeurs proposées par défaut sont avec les mêmes côtes, le résultat calculé vous permet de vérifier que le calcul est juste.
Distance de mesure à d = 100 cm.
Le haut-parleur du bas est placé à hhp = 50 cm du sol.
Le haut-parleur du haut est placé à 150 cm du sol, pour le cas avec deux haut-parleurs.
Le micro est placé à hm = 85 cm du sol.

La distance entre l'enceinte et le point de réflexion avec le sol est d1 = d * hhp / ( hm + hhp).
La distance entre le point de réflexion avec le sol et le micro est d2 = d - d1.
Nous pouvons ensuite facilement calculer les trois longueurs, HP au sol, sol au micro, HP au micro, et la différence de longueur = (HP au sol + sol au micro) - HP au micro.
La différence de phase en degré est 360 * différences de longueur) / C * F.

 

Valeurs de calculs :

Hauteur du HP du bas par rapport au sol ( en cm ) : 
Hauteur du HP du haut par rapport au sol ( en cm ) : 
Recul du HP du haut par rapport à l'optimum ( en cm ) : 
Hauteur du Micro par rapport au sol ( en cm ) : 
Distance horizontale du HP au micro ( en cm ) : 
Atténuation quand la distance double ( en dB ) : 

 

 

HP du bas :

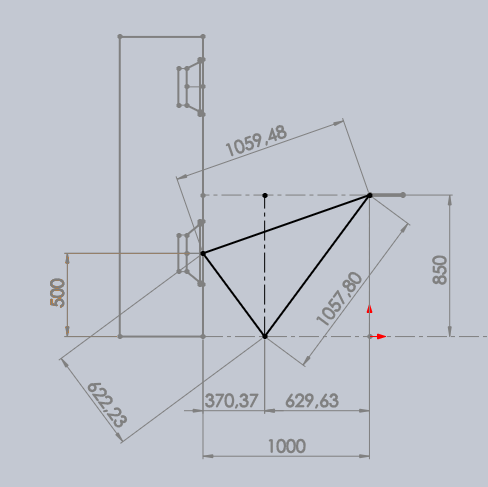
Hauteur micro différente de la hauteur HP

Valeurs calculées pour le HP du bas :

Distance horizontale du HP du bas au micro = 100 cm.
Distance horizontale du HP du bas au sol = 37.0 cm.
Distance horizontale du sol au micro pour le HP du bas = 63.0 cm.

Distance en biais du HP du bas au micro = 105.9 cm.
Distance en biais du HP du bas au sol = 62.2 cm.
Distance en biais du sol au micro pour le HP du bas = 105.8 cm.
Différence de phase en degré côté sol pour le HP du bas = 0.6500 * F.

Atténuation avec la différence de longueur = -4.0 dB

 

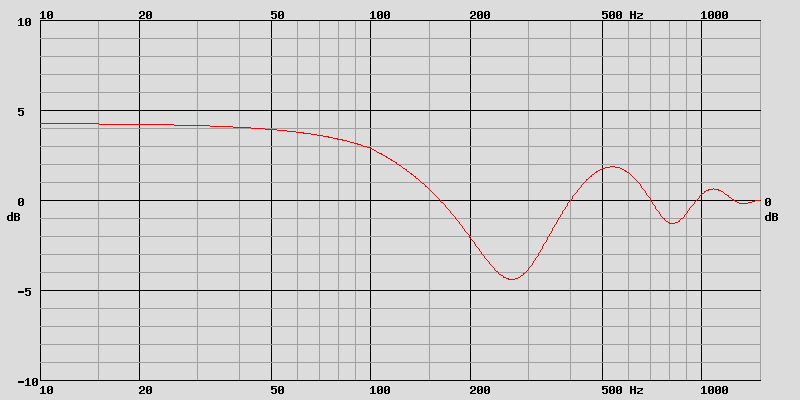
Somme du rayonnement direct et de la réflexion au sol, juste le HP du bas.

somme du rayonnement direct et réflexion au sol

 

HP du haut :

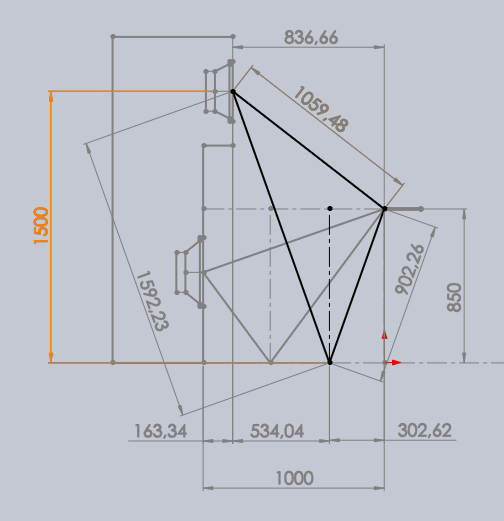
Hauteur micro différente de la hauteur HP

 

Valeurs calculées pour le HP du haut :

Il y a une hauteur limite, qui est égale à la hauteur du micro plus la distance en biais du HP du bas au micro = 190.9 cm.
A cette distance limite, le HP du haut est à la verticale du micro.
La solution est d'éloigner le micro.
Cette hauteur peut être plus grande avec un recul du haut-parleur par rapport à l'optimum théorique.

Recul du HP par rapport à la valeur idéale = 0 cm.
Variation de la phase à 100 Hz = 10.4°.
Variation de la phase à 500 Hz = 52.2°.

Distance horizontale du HP du haut au micro = 83.7 cm.
Distance horizontale du HP du haut au sol = 53.4 cm.
Distance horizontale du sol au micro pour le HP du haut = 30.3 cm.

Distance en biais du HP du haut au micro = 105.9 cm.
Distance en biais du HP du haut au sol = 159.2 cm.
Distance en biais du sol au micro pour le HP du haut = 90.2 cm.
Différence de phase côté sol pour le HP du haut = 1.5030 * F.
Différence de phase pour les 0 cm = 0.0000 * F.

Atténuation avec la différence de longueur = -7.4 dB

 

Somme du rayonnement direct et de la réflexion au sol, juste le HP du haut.

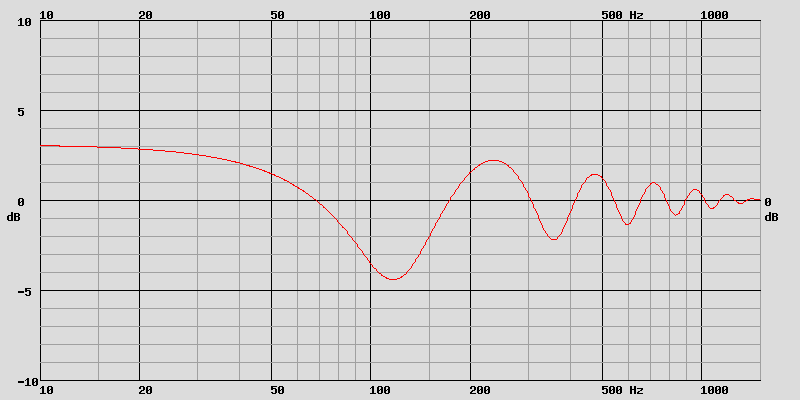
somme du rayonnement direct et réflexion au sol

 

Avec les deux HP :

Il faut faire la somme des deux calculs, en tenant compte de la phase à chaque fréquence.
Le haut-parleur du haut a été avancé pour être à la même distance du micro que le haut-parleur du bas, dans le but d'avoir une bonne mise en phase sur les impulsions.

 

Somme du rayonnement direct et de la réflexion au sol, pour les deux HP.
Rouge : HP du bas. Vert : HP du haut. Bleu : Somme des deux HP, rouge + vert avec la phase.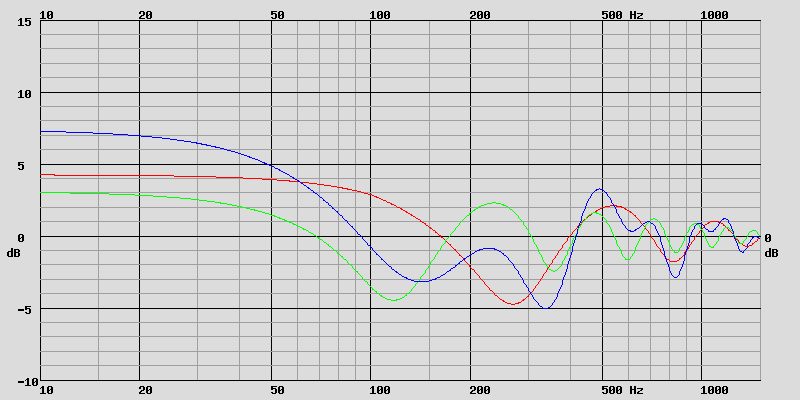

somme du rayonnement direct et réflexion au sol

 

Il fallait le calculer pour voir ce que cela donne, un 2e haut-parleur placé en hauteur est une fausse bonne idée à oublier au plus vite...
Par contre un 2e haut-parleur placé très proche du sol améliore sensiblement les choses.
Très près du sol, c'est 5 cm environ, c'est le HP dirigé vers le sol.

 

Les recommandations de bon sens :

Les valeurs indiquées sont les valeurs calculées dans la partie "Calculez votre cas réel".
Si vous changez les valeurs de calculs dans la rubrique précédente, les valeurs calculées seront modifiées.

Si vous placez le micro à raz du sol, à moins de 10 cm du sol, vous n'aurez pas de trou dans la réponse.
Et si la solution n'était pas, pendant la mesure MMM, de passer justement à raz du sol avec le micro ?
Actuellement c'est une idée à creuser, pour validation ou pour élimination de l'idée...

 

Une exception soigneusement vérifiée :

J'ai vérifié à l'écoute qu'il n'était pas possible de corriger les creux dans l'image ci-dessous, la mesure a été faite à 50 cm, l'écoute se fait à 4 m, les creux et bosses mesurés à 50 cm ne correspondent pas à ceux à 400 cm.
En rouge sans correction, en bleu avec une correction acceptable et validée à l'écoute.
Ce point est aussi indiqué dans le chapitre que faut-il corriger, qui pose les règles pour la correction par convolution.
Si vous partez d'une mesure au point d'écoute, la conclusion sera différente, et la correction sans doute possible, à vérifier à l'écoute.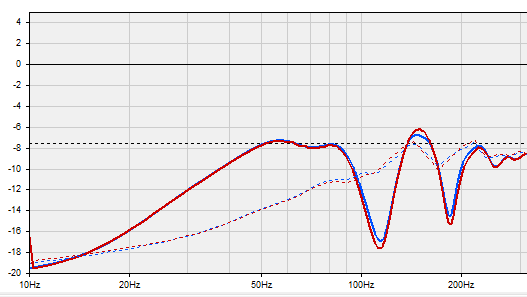

Correction homéopatique ces creux dans la courbe de réponse, creux dû au sol et au plafond

 

Pourquoi ne faut-il pas corriger le trou ?

Rappelons pourquoi nous avons un trou dans la courbe de réponse :
Il y a un signal direct qui va du HP au micro avec une distance entre les deux.
Il y a un signal réfléchi qui va du HP au sol et au micro, avec une distance plus grande.
À certaines fréquences les deux signaux arrivent en opposition de phase, il y a un trou dans la courbe de réponse.

Si vous essayez de combler le trou, le signal direct sera plus fort, le signal réfléchi sur le sol aussi, le trou dans la courbe de réponse sera le même...
Vouloir combler le trou est une grosse erreur, une solution est d'atténuer la réflexion, ce qui est très difficile compte tenu des longueurs d'onde.
Marcel Roggero avait fait sur son installation une fosse devant ses enceintes dans sa pièce dédiée, fosse remplie d'amortissement, c'est une solution efficace, Marcel est le seul à ma connaissance à l'avoir utilisé.
Une autre solution est d'ajouter un autre haut-parleur, placé à un autre endroit, de telle sorte qu'il n'y ait pas de trou au même endroit.
Un calculateur pour cette solution serait bienvenu, il a été réalisé, il n'y a pas de solution satisfaisante.

 

Comment vérifier que boucher le trou ne sert à rien ?

Ce n'est pas compliqué, quoi que, il suffit de mesurer à travers les corrections.
Quand vous avez passé du temps à corriger, et que vous vous rendez compte que localement les corrections sont totalement inefficaces, cela fit mal sur le coup...
Retirez les corrections qui ne servent pas, vous envoyez de la puissance dans le HP pour rien...

 

Deux mesures réelles :

Mes 420-8B, en enceinte close, mesurés à 86 cm du cache noyau, HP et micro à 85 cm du sol.
Le creux de 12 dB à 100 Hz, avec une étendue entre 45 et 200 Hz, est parfaitement visible.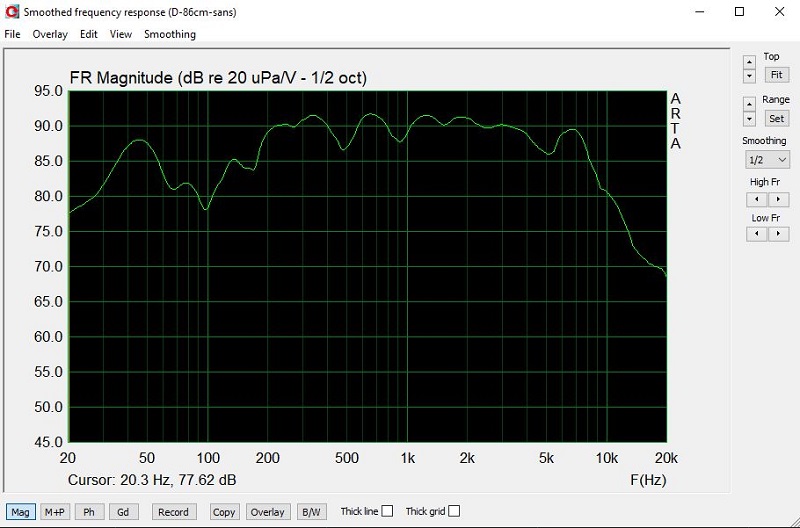

Mesure des 420-8B à 86 cm

 

Mes 420-8B mesurés à 2 cm du cache noyau, bande passante limitée à l'affichage à 400 Hz.
Plus de creux, et même une petite bosse très douce à 145 Hz, bosse qu'il faudra certainement corriger.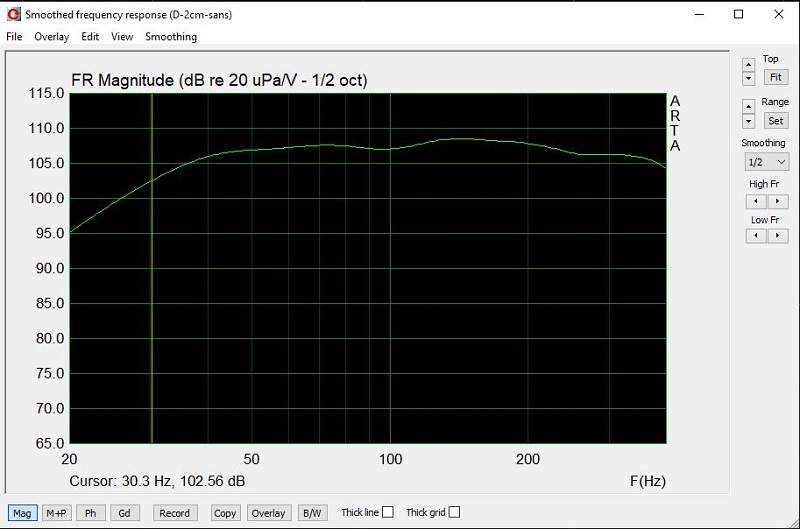

Mesure des 420-8B à 2 cm

 

Image de la mesure des 420-8B à 3 cm

 

La solution, enceinte close :

Le lien de la Première présentation des webinars Klippel page 15 (distance R en pouces, 1 pouce = 2.54 cm) nous montre qu'il n'y a pas de formule qui s'applique pour trouver l'atténuation entre une mesure à très courte distance et une autre plus loin.
La formule Atténuation_du_grave = 20 * LOG( 86 / 2 ) = 32.7 dB ne marche pas du tout à partir d'une mesure à très courte distance.
D'après le graphique du lien ci-dessus, la formule semble marcher au-dessus de 4 pouces, environ 100 cm, en sachant que la distance changera en fonction de chaque pièce.
Nous devons faire l'alignement sur le niveau de la bosse vers 50 Hz, puis essayer à l'écoute diverses valeurs autour de ce réglage.

Importer les deux mesures, à 2 cm et à 86 cm dans EXCEL.
Si vous regardez vers 250 Hz, la mesure à 86 cm est à 90 dB et celle à 2 cm est à 107 dB, soit 17 dB de différence, loin des 32.7 dB théoriques.
Pour une mesure très proche, l'atténuation n'est pas en 1 / distance2.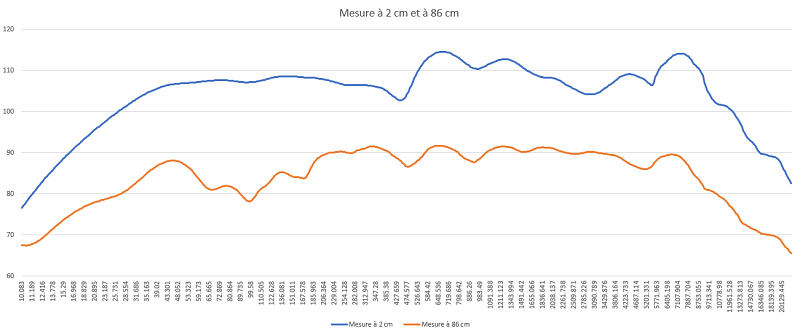

Mesure des 420-8B à 2 cm et 86 cm sans correction

 

Abaisser la mesure à 2 cm pour l'aligner pile sur la bosse à 43 Hz.
Ce n'est pas exactement le sommet, c'est la tangente des deux courbes, et c'est "à l'œil".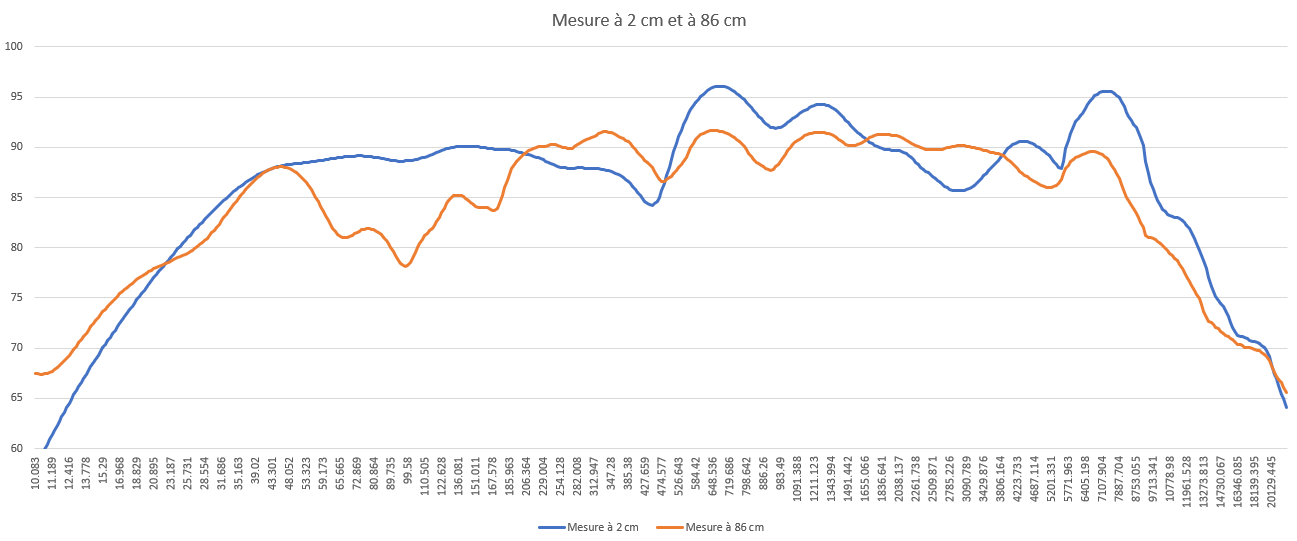

Mesure des 420-8B à 2 cm et 86 cm au même SPL

 

Couper les deux mesures à 205 Hz et fusionner.
205 Hz, parce que c'est là que les deux courbes se raccordent au mieux.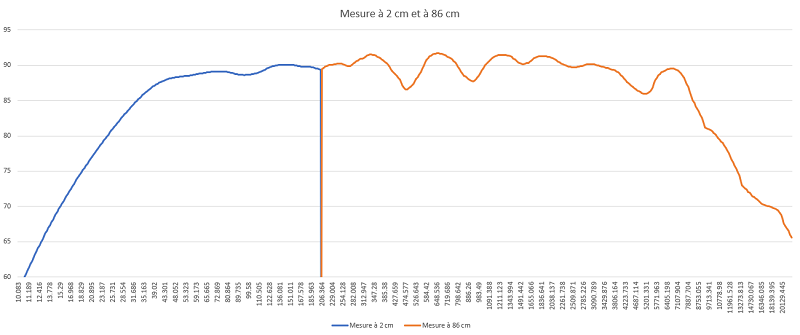

Mesure des 420-8B à 2 cm et 86 cm au même SPL, coupée à 250 Hz

 

Essayer à l'écoute plusieurs niveaux de graves.
Il faut ajuster la fréquence de passage d'une courbe à l'autre, je ne l'ai pas fait dans cet exemple.
L'optimum à l'écoute se trouve vers -0.65 dB avec -0.60 dB < -0.65 dB > -0.70 dB dans mon cas.
Pourquoi ?
Je n'en n'ai aucune idée, seule l'écoute à raison quand les critères d'écoute sont bons...
C'est avec -0.65 dB que la scène sonore est la plus grande, signe d'une grande qualité.

Notez qu'en mettant le grave à -0.65 dB, après le passage dans rePhase et la linéarisation sur le "0 dB", cela se traduit en pratique par un petit boost très raisonnable du grave jusque 200 Hz environ.
200 Hz est la fréquence à laquelle la mesure à 86 cm prend le relais.
La mise au point précise apporte un vrai plus à l'écoute.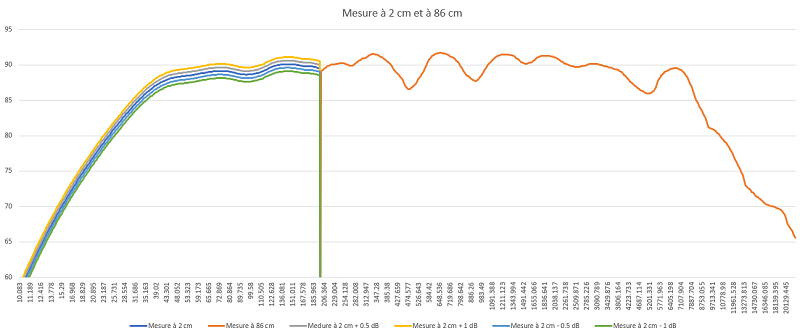

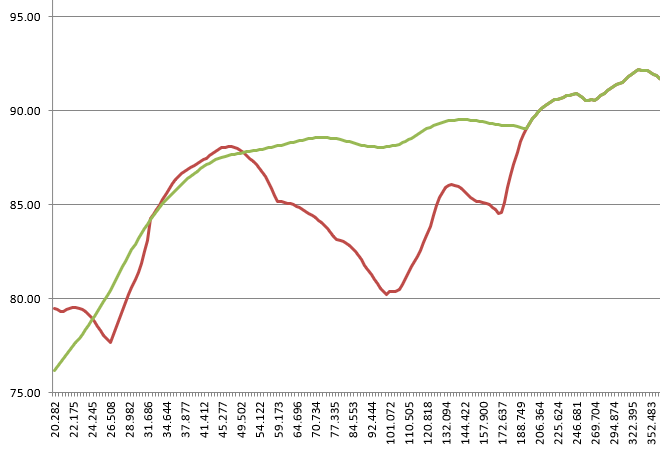
Mesure des 420-8B à 2 cm et 86 cm au même SPL, plusieurs niveaux Mesure des 420-8B à 2 cm et 86 cm, 2 cm à -0.6 dB

 

Nous avons une réponse parfaitement exploitable pour corriger dans rePhase.
L'absence de niveau de référence de la mesure à 86 cm par rapport à celle à 2 cm nous oblige à faire plusieurs essais à l'écoute pour trouver les bonnes valeurs, celles qui marchent le mieux à l'écoute, avec toute la subjectivité qui va avec.
Nous sommes presque dans un système à deux voies, avec le réglage du niveau du grave par rapport à celui du médium aigu !!!

Dans rePhase, il n'y a pas photo entre les anciennes mesures à 84 cm et les nouvelles à 86 et 2 cm.
Même si je ne corrigeais pas entre 50 Hz et 200 Hz avec la mesure à 84 cm, j'ai trouvé une bosse de +3.5 dB à 145 Hz avec la mesure à 86 et 2 cm, et ça c'est audible...

Je vais insister lourdement : si vous n'avez que la seule mesure "à 84 cm", vous ne corrigez pas entre 50 et 200 Hz...
Si votre logiciel automatique corrige le creux entre 50 et 200 Hz, jetez-le, ou corrigez à la main.
En écrivant ces propos, je vais me mettre à dos les marchands de logiciels automatiques, et les cadors des forums, mais c'est pour la bonne cause.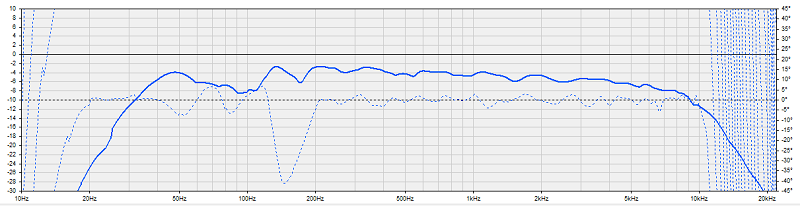

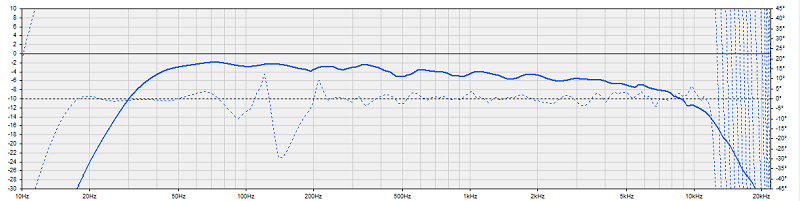
Mesure et correction des 420-8B à 84 cm dans rePhase Mesure et correction des 420-8B à 86 et 2 cm dans rePhase

 

Bonne mesure et bonne distance de mesure :

J'ai fait une série de mesures entre 2 et 20 cm, en ne déplaçant que le micro entre chaque mesure, sans toucher au bouton de volume entre les mesures.
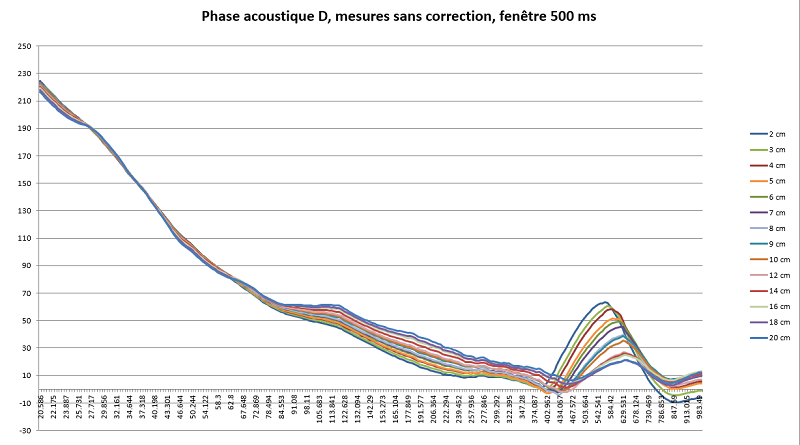
Une importation dans EXCEL permet de superposer les mesures, aussi bien pour la réponse que pour la phase acoustique.
Sur les réponses, le baffle step commence à se voir pour les mesures supérieures à 10 cm entre 200 et 400 Hz.
La phase acoustique ne montre rien de significatif.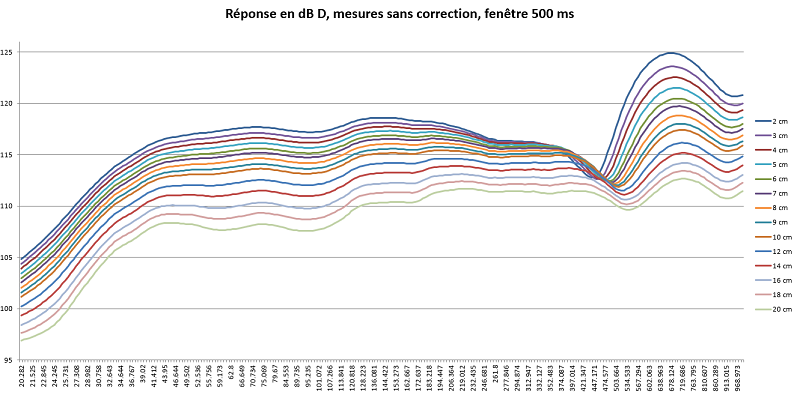

Mesure de la réponse entre 2 et 20 cm Mesure de la phase totale entre 2 et 20 cm

 

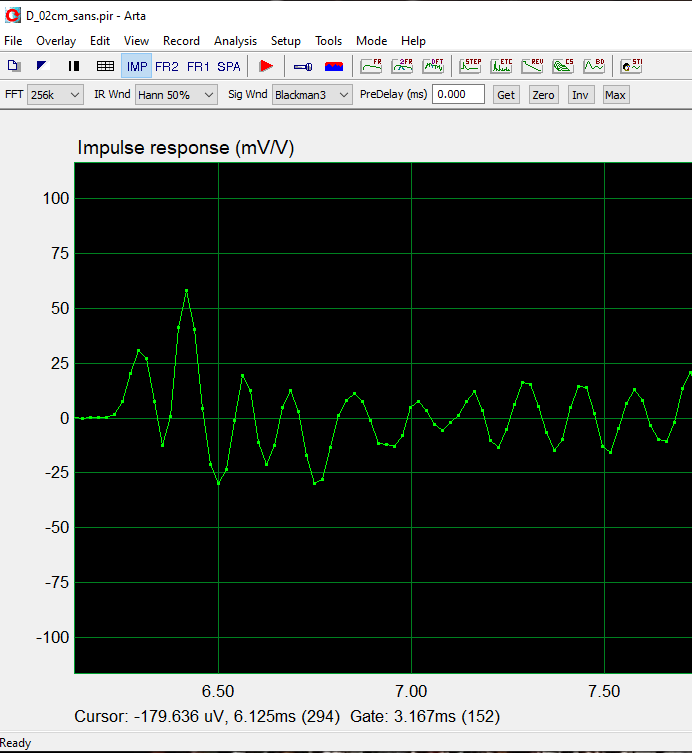
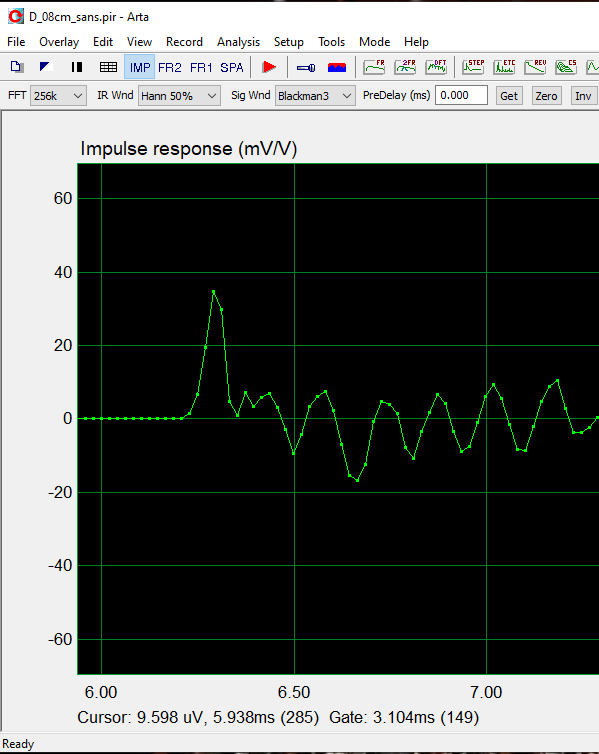
À côté de la réponse et la phase acoustique totale, l'impulsion et le step donnent des informations intéressantes.
Mais c'est la mesure d'un haut-parleur large bande qui monte jusque 8000 Hz sans correction, alors que la mesure proche n'est valable que jusque 330 Hz.
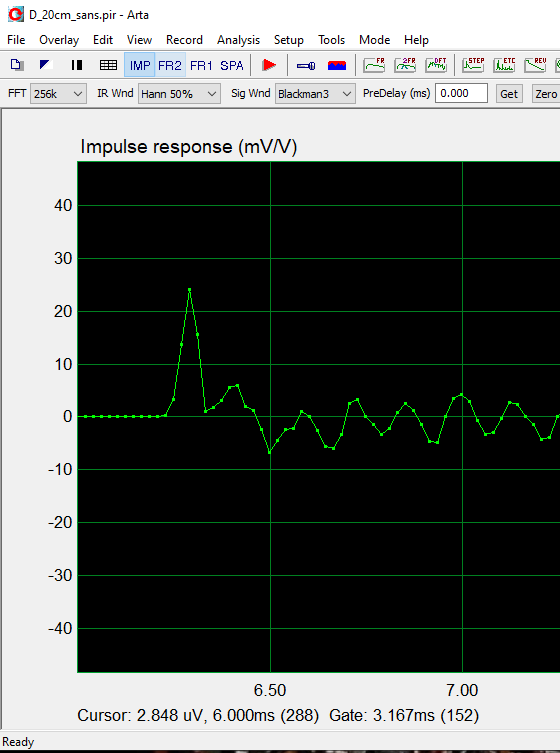
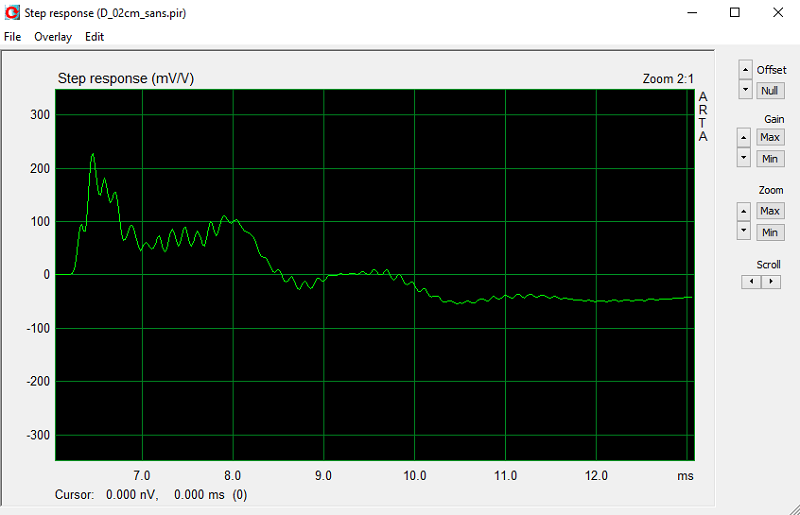
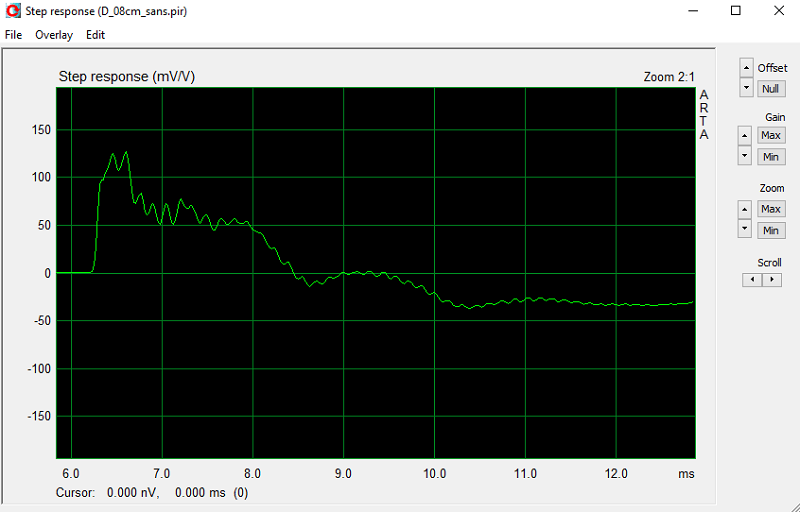
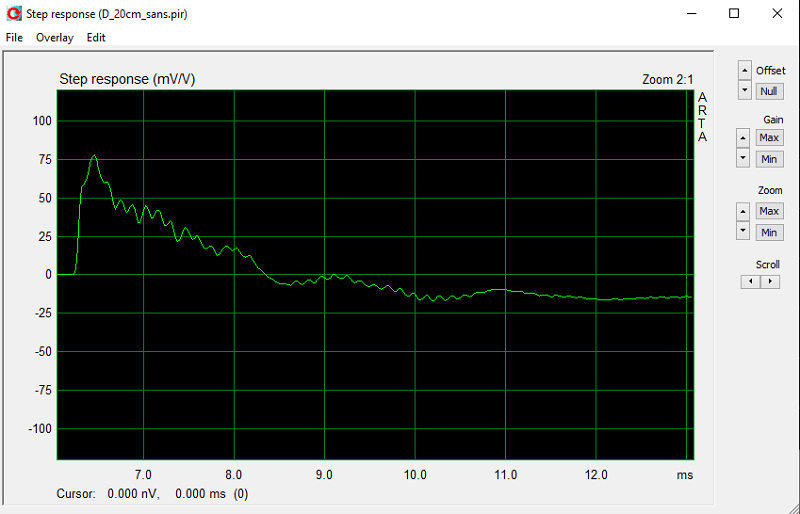
La mauvaise qualité des mesures impulsion et step à 2 cm n'est pas dans le domaine de validité de la mesure, on constate et on ignore !!!

 

Impulsion :

Impulsion de la mesure à 2 cm

 

Impulsion de la mesure à 8 cm

 

Impulsion de la mesure à 20 cm

 

Step :

Step de la mesure à 2 cm

 

Step de la mesure à 8 cm

 

Step de la mesure à 20 cm

 

Conclusion :

Le but de la mesure proche du haut-parleur était de supprimer le trou dans la réponse entre 45 et 200 Hz.
Si nous ne regardons que la réponse ou la phase acoustique totale, la mesure à 2 cm est génial, la correction est un succès.
Il ne faut pas regarder l'impulsion ou le step, la mesure large bande qui est réalisée n'est plus valable au-dessus de 330 Hz.
Le seul doute qui reste est la distance, 2 cm ou 4 cm, puisque :

  • Joe d'Appolito dans son livre parle de 0.11D, c'est-à-dire 3.7 cm.
  • Klippel parle de 11% du rayon : 0.11 * 16.7 = 1.8 cm pour mon ALTEC 420-8B.

 

Mickael m'a transmis les informations suivantes :

Le PDF AN39 de Klippel Merging Near and Far Field Measurements indique dans la partie Closed Box (Enceinte close) :

Closed box.
The measurement microphone should be placed normal and as close as possible to the center of the dust cap to ensure a quasi anechoic measurement caused by the high level differences between direct sound and room reflections.
By keeping the micro-phone distance less than 11% of the effective cone radius a, the measurement error will be less than 1dB.
To prevent damage to the driver or the microphone, the maximum excursion should be determined first and considered while placing the microphone

La traduction de Mickael est :

Boîte fermée.
Le microphone de mesure doit être placé normalement et aussi près que possible du centre du capuchon anti-poussière pour assurer une mesure quasi anéchoïque causée par la haute différence de niveau entre le son direct et les réflexions de la pièce.
En gardant le micro a une distance inférieure à 11% du cône effectif de rayon a, l'erreur de mesure sera moindre que 1dB.
Pour éviter d'endommager le haut-parleur ou le microphone, l'excursion maximale doit être déterminée en premier et prise en compte lors du placement du micro.

 

La solution, enceinte Bass reflex :

Il va falloir faire une 3e mesure dans l'axe de l'évent, à la même distance que pour la mesure proche du HP de grave.
Le micro doit se déplacer dans le même plan vertical entre les deux mesures.

Le niveau de cette mesure sera différent du niveau relevé à 2 cm du haut-parleur, parce que la surface de l'évent est différente de celle du haut-parleur.
Soit Sd : la surface du haut-parleur, et Sev : la surface de l'évent.
Joe d'Appolito indique dans son livre : Correction = 20 * LOG( racine( Sev / Sd ) ).
Ce calcul fixe les niveaux entre la mesure à courte distance du HP, et celle en face de l'évent, un évent inefficace se voit ainsi très facilement.

Vous importez les 3 courbes dans EXCEL, vous corrigez le niveau à courte distance par rapport au niveau plus loin du HP, et vous gardez les parties utiles de chacune des courbes.
Exactement comme une enceinte close, mais avec une courbe de plus dont le niveau est fixé par calcul.
Quand j'aurai un exemple mesuré, j'en ai un, j'ajouterai des images pour illustrer et confirmer.

 

Un grand merci pour votre visite. --- Retour direct en haut de la page ---

Logo Dôme acoustique

Un grand-père facétieux disait à ses petits enfants que le grand truc blanc tout en haut du Puy-de-Dôme était un thermomètre géant : Quand il deviendra tout rouge il faudra vite se sauver, parce que le volcan va se réveiller !!!

Malgré les apparences, ce site internet n'est que celui d'un amateur passionné auvergnat.
"Amateur" doit être compris dans le sens "non professionnel", dans l'aspect financier de l'approche : Je ne vis pas des revenus de cette passion.
"Amateur" doit être compris dans le sens ou rien ne m'oblige à vous répondre, si vous êtes désagréable. C'est rare, mais le cas arrive de temps en temps.

Il y a un savoir-vivre élémentaire qui consiste à demander l'autorisation avant de reprendre tout ou partie de ce qui est écrit dans ce chapitre.
Je vous donnerai l'accord, demandez-le simplement pour être en règle. Sont exclues les demandes extravagantes, les demandes de copie de ma base de données haut-parleurs.

Contrôle de validation W3C du code HTML 5 de la page, copiez l'adresse de la page avant de cliquer sur le lien.
Contrôle de validation W3C des CSS de la page, copiez l'adresse de la page avant de cliquer sur le lien.
Ce sont deux outils de contrôle pour le webmaster du site Dôme Acoustique, c'est inutile pour les utilisateurs.
Avoir le lien dans chaque page est plus simple pour les retrouver.