2-1-1-13 : L'optimisation par le rendement

Mise à jour : 27 juin 2023, Antimode 11.

 

Pourquoi une autre optimisation ?

Il faut remonter à plusieurs années en arrière, au début des années 2000, à l'époque j'avais des enceintes avec évent.
J'ai cherché à l'écoute, en gardant l'accord de l'évent constant, quel était le volume qui donnait le meilleur résultat d'écoute.
Lorsque la variation de volume, par rapport au réglage de l'évent initial, devenait trop importante, je refaisais un réglage d'évent à l'écoute avant de continuer à faire varier le volume.
Pour tous les haut-parleurs essayés avec un Qts > 0.38, (pas tant que cela au final), je trouvais un volume qui donnait de meilleurs résultats d'écoute que les autres.
Pour tous les haut-parleurs essayés avec un Qts > 0.38, le volume trouvé correspond à celui donné par le calcul ci-dessous, l'optimisation par le rendement.

Ce chapitre a été retiré deux fois pendant un moment, pour de mauvaises raisons.
En précisant bien les conditions d'utilisation, et les conditions de non-utilisation, le volume donné par l'optimisation par le rendement ne pose pas plus de problèmes que n'importe quelle autre optimisation.
Un alignement, même l'optimisation par le rendement, s'il est bien calculé est toujours préférable a un montage d'un haut-parleur dans une enceinte sans le moindre calcul, ou en se plantant lamentablement avec un logiciel sans garde fou, ou encore en montant dans une enceinte avec évent un haut-parleur qui n'est absolument pas prévu pour cela...

Le terme alignement est juste avec le volume calculé et Fb = Fs, sans chercher Fb à l'écoute.
Fs est à mesurer le haut-parleur à l'air libre.
Avec ces conditions, l'optimisation par le rendement ne peut pas être critiquée sur son principe.

 

L'optimisation par le rendement.

Il faut se souvenir qu'un haut-parleur est un convertisseur qui transforme l'énergie électrique de l'ampli en énergie acoustique : le son.
Toutes conversions se font avec un rendement.
Il est possible de calculer le rendement du haut-parleur à partir des paramètres de THIELE et SMALL, et dans une enceinte de volume donnée.

L'optimisation par le rendement, consiste à trouver le volume pour que le rendement du haut-parleur dans son enceinte avec un accord Fb = Fs soit égal au rendement du haut-parleur calculé avec les paramètres THIELE et SMALL.
C'est le seul paramètre qui est en parfaite corrélation avec les essais de recherche de volume optimum.

Les paramètres utilisés pour les calculs sont :

• C = Vitesse du son = 343.707 m/s à 20° Celsius.
• Ro = Masse volumique de l'air = 1.194 kg/m³à 40% d'humidité relative
• Vb = Volume de l'enceinte en m³
• Fs = Fréquence de résonance du haut-parleur en Hz.
• Vas = Volume d'air équivalent à l'élasticité de la suspension en m³
• Qts = Coefficient de surtension total du haut-parleur.
• BL = Facteur de force en N/A.
• Re = Résistance en continu du haut-parleur en Ohms.
• Sd = Surface mobile en m²
• Mms = Masse mobile en kg.

Le rendement du haut-parleur à partir des paramètres de THIELE et SMALL est :
RV = ( Ro / 2 / Pi / C ) * ( BL² / Re ) * ( Sd² / Mms² )

Le rendement du haut-parleur dans son enceinte (à la fréquence F3) est :
RB = K * R1 / Qts * F₃³ * VB
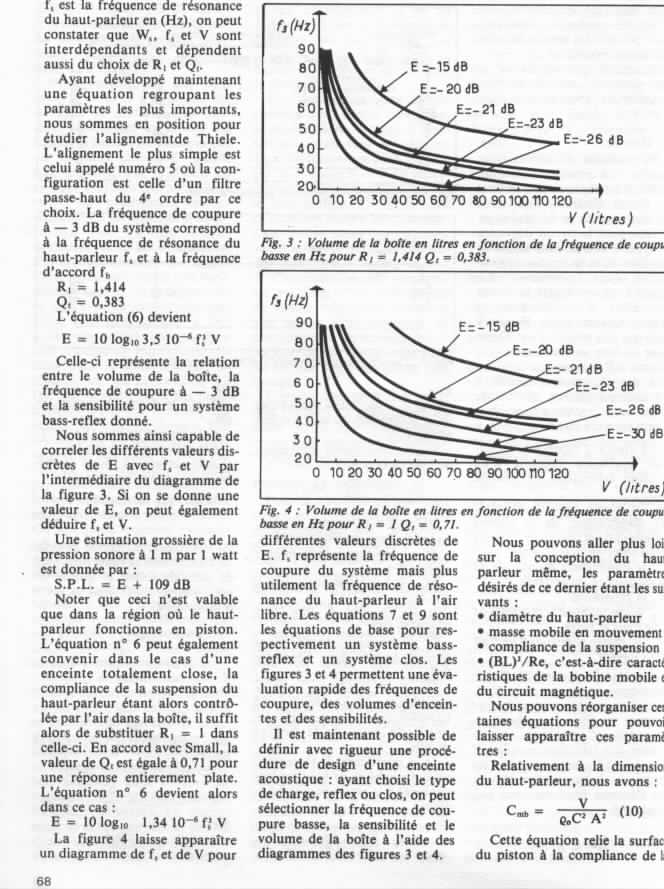
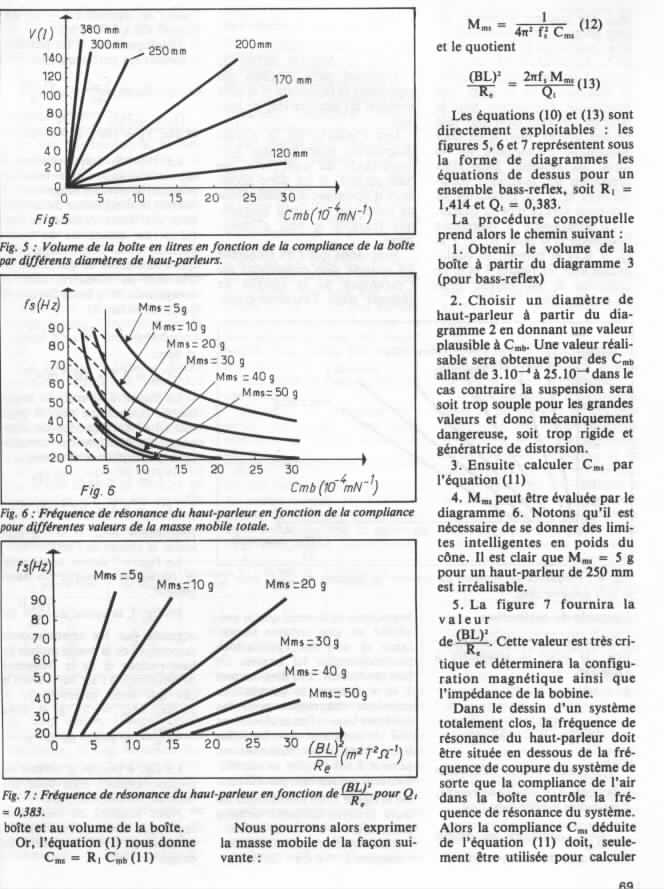
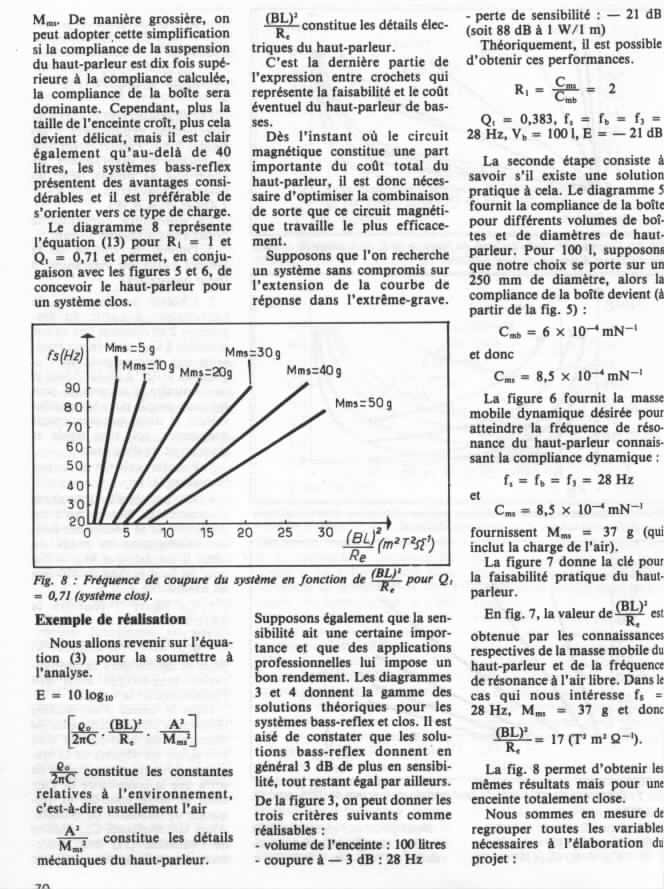
Cette équation est tirée d'un article de l'Audiophile, numéro 24 première série, "une enceinte donnée, un haut-parleur unique", voir à la fin de ce chapitre.

Avec : K = 4 * Pi² / C³,
R1 = Cms / Cmb = Vas / Vb,
F₃ = Fs * racine( Vas / Vb ),
L'équation de F3 vient du livre de Charles-Henri DELALEU : "L'optimisation des haut-parleurs et enceintes acoustiques", dans le chapitre Bass-reflex, et dont je ferais bien de rajouter le scan avec l'article de l'Audiophile.

Après remplacement et simplification, cela donne :
RB = ( 4 * PI² / C³ ) * ( Vas^5/2 / Vb^3/2) * ( Fs³ / Qts)

L'optimisation par le rendement consiste à dire : Le rendement du haut-parleur calculé avec les paramètres de THIELE et SMALL = Le rendement du haut-parleur dans son enceinte.
Ro / 2 / Pi / C * BL² / Re * Sd² / Mms² = 4 * Pi² / C³ * Vas^5/2 / Vb^3/2 * Fs³ / Qts

Après regroupement et simplification, l'équation devient :
Vb = ( ( 8 * Pi³ / C² / Ro ) * VAS^5/2 * ( Fs³ / Qts) * ( Re / BL² ) * ( Mms² / Sd² ) )^2/3

Francis Brooke (site Francisaudio) m'a laissé le commentaire suivant :

Juste un petit commentaire sur ton calcul de VB par l'égalité des rendements a vide et en charge :
Si dans la formule du calcul à vide tu remplaces BL² / Mms et Sd² / Mms par leurs valeurs respectives en fonction de Vas et Qes tu obtiens :
Rendement à vide = 4 * Pi² / C³ * Fs³ * Vas / Qes.
L'égalité des rendements est alors vérifiée pour Vb = Vas * ( Qes / Qts )^2/3.
Cette expression me paraît plus simple à utiliser que celle que tu proposes.

La remarque est pertinente et juste, l'équation est beaucoup plus simple.
Bien souvent les valeurs de BL, Mms et S données par les constructeurs sont fausses, ou pas homogènes avec les autres données.
Cette équation règle tous les problèmes.
À adopter sans réserve, merci, Francis.

L'équation peut s'écrire un peu autrement. Qts = Qms * Qes / ( Qms + Qes ).
En remplaçant dans l'équation précédente, on obtient :

Vb = Vas * ( ( Qms + Qes ) / Qms )^2/3

Dans certaines documentations des fabricants, le calcul du Qts est parfois faux.
Cette écriture vous garantit un résultat toujours juste.

Dans le cas d'un filtre passif avec le haut-parleur, la résistance série du filtre, les selfs en série avec le haut-parleur, doit être prise en compte.
Si RF est la résistance en série :
Qes = Qes * ( Rf + Re ) / Re.
Qts = Qms * Qes / ( Qms + Qes ).

 

Une erreur très fâcheuse.

Dans le paragraphe ci-dessus, j'ai indiqué que le rendement du haut-parleur dans son enceinte (à la fréquence F3) est :
RB = K * R1 / Qts * F₃³ * VB
avec : K = 4 * Pi² / C³,
R1 = Cms / Cmb = Vas / Vb,
F₃ = Fs * racine( Vas / Vb )

F₃ ne serait pas la variable à utiliser, mais F_s
L'équation devient : RB = K * R1 / Qts * F_s³ * VB
Si nous remplaçons R1 par sa valeur, l'équation devient après simplification par Vb : RB = K * Vas / Qts * F_s³
Si on considère d'autre part que Qms est très supérieur à Qes, alors Qes est très proche de Qts : RB = K * Vas / Qes * F_s³
En remplaçant K par sa valeur nous revenons à l'équation du rendement du haut-parleur à vide : 4 * Pi² / C³ * Fs³ * Vas / Qes.

En remplaçant F3 par Fs, nous éliminons toutes possibilités d'optimisation par le rendement...
Qes très petit devant Qms n'est pas toujours vrai quand on regarde les T&S d'un grand nombre de haut-parleurs.

J'ai du mal à croire que Fs soit la valeur à prendre.
D'un autre côté, je n'ai jamais lu qu'en changeant Vb ou Fb, le rendement du haut-parleur changeait.

Si au lieu de prendre F_s ou F₃ nous prenions F_{à -3 dB} calculé avec la courbe de réponse, alors il y a une solution à l'optimisation par le rendement, solution qui peut être trouvée avec un calcul par itérations.
Une solution mathématique basée sur des équations qui n'ont pas de sens ne doit pas être retenue.

 

Utilisation de l'optimisation par le rendement.

Aucune utilisation, avoir pris F3 à la place de Fs est une erreur.
Comme dans l'article de l'Audiophile, il y a aussi une erreur sur la puissance de Fs ou F3, un carré au lieu d'un cube, la démarche m'avait semblé bonne.

Pourquoi laisser un chapitre qui ne sert à rien ?
Parce que c'est le chapitre "Poil à gratter" de certains forumeurs particulièrement déplaisants.

 

L'article de l'audiophile.

 

 

 

 

 

 

Dôme Acoustique