Page affichée à 19:52:32
vendredi 19 avril 2024
Ce site n'utilise pas de cookie.Dôme acoustique Compteur pour tout le site : 13 982 592
Nombre actuel de lecteurs : 70.Faire
un don
par
PayPalLe site de Dominique, un amateur passionné
2-6-3-2 : Le filtre à 18 dB, 4/5
Mise à jour : 31 octobre 2023
Les outils de calculs des filtres fonctionnent beaucoup mieux si vous avez choisis les HP dans les tables.
Pour les filtres avec HP relais, le choix préalable des HP est une nécessitée absolue.
Si vous arrivez sur cette page sans avoir choisi les HP, je vous invite à Aller faire votre choix des HP à filtrer, vous arriverez au chapitre "Impédance à la fréquence de coupure" ou vous aurez à choisir le HP de graves, puis le filtre et le tweeter deux chapitres après.Avant d'utiliser les formules ou les résultats de calculs de ce chapitre, je considère que vous avez pris connaissance du chapitre "Les limites du calcul des filtres passifs", et que vous avez compris la confiance relative qu'il faut avoir dans les résultats.
Les calculs effectués sont justes en faisant l'hypothèse que les HP sont assimilables à des résistances pures, ce qui est loin d'être le cas en pratique.L'idée que le même filtre passif peut convenir à plusieurs haut-parleurs est totalement fausse : Entre l'impédance à la fréquence de coupure qui varie avec l'inductance de la bobine mobile, les corrections de courbe de réponse intégrée au filtre (et non calculable ici), les atténuations différentes d'un HP à l'autre, les filtres sont toujours différents lorsqu'ils sont bien au point.
Les outils de ce site sont des calculateurs, les simulateurs sont beaucoup plus précis mais demandent d'avoir mesurer la courbe de réponse et de phase acoustique d'un coté, la courbe d'impédance et de phase électrique de l'autre, les HP montés dans leur enceinte définitive, pour pouvoir travailler.
J'insiste "lourdement", avec un calculateur vous devez finir la mise au point à l'écoute.Le chapitre "Mise au point des filtres" vous aidera à passer de la théorie à la pratique.
Les filtres à 2 voies à 18 dB/octave.
Filtre à 18 dB/octave avec raccord à -3 dB :
S'il n'y avait pas la courbe en coïncidence qui est à +3 dB à 1000 Hz, et au-dessus de +1 dB de 500 à 2000 Hz, ce serait un très bon filtre.
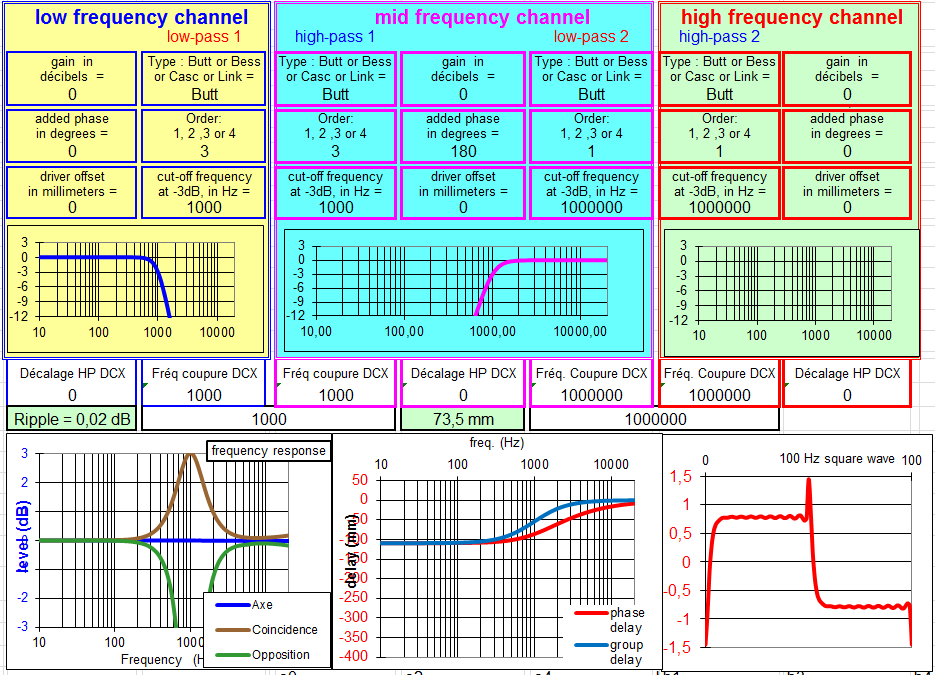
Filtre à 18 dB/octave avec raccord à -5 dB :
À l'écoute les résultats sont bons.
Je l'ai longtemps considéré comme étant le meilleur filtre en valeur absolu, si vous avez besoin de pentes raides.
Pourtant à la simulation, et si vous pouvez vous contenter de pentes à 12 dB/octave, je pense qu'il y a mieux avec le Linkwitz Riley.
Par rapport au raccord à -3 dB, ce qui est gagné sur la courbe en coïncidence est un peu perdu sur la réponse dans l'axe et le délai de groupe.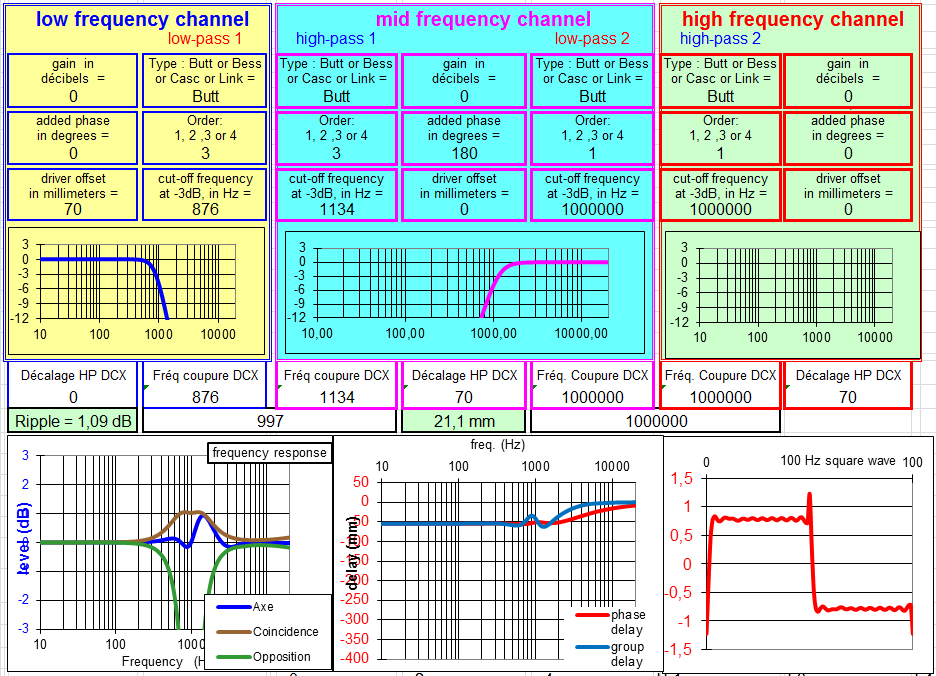
2-6-7-4 : Choix des selfs :
Mise à jour : 7 novembre 2023, Antimode 11.
Selfs à air ou selfs sur noyau métallique ?
Cette copie d'un courriel de Jean-Claude TORNIOR illustre parfaitement l'intérêt d'utiliser des selfs sur noyau métallique.
Outre l'aspect faible résistance interne, l'aspect prix est lui aussi plus que très intéressant.
Ce courriel est recopié ici avec l'accord écrit de son auteur, dans le plus strict respect des Règles déontologiques du site.Bonjour Dominique,
Je me suis permis de me balader un peu sur votre site et j'ai constaté à la vision de votre "caisse de selfs" qu'il n'y avait que des selfs à air.
Je me permets, à ce sujet, de vous apporter quelques réflexions personnelles.Il est en effet d'usage dans le "Monde Audiophile" de considérer que les selfs à air sont la panacée, au même titre que le fil de LITZ ( qui n'a pas été créé par le compositeur !... Hum...), les conducteurs monobrin, le fil d'argent et bien d'autres fantômes qui trouvent leurs sources dans une certaine logique de bazar dont on ne connaît pas précisément les sources.
En ce qui concerne les selfs, cette réputation découle d'une époque ou les matériaux ferreux utilisés avaient des propriétés médiocres qui faisaient que l'on pouvait les saturer lors de fortes puissances avec l'incidence d'une dérive des valeurs de l'inductance à ces fortes puissances.
Ce n'est plus le cas aujourd'hui avec l'utilisation de plaques de noyaux en mumétal ou en ferrite.
Depuis de nombreuses années, de très sérieux constructeurs utilisent exclusivement des selfs à noyaux (CABASSE, KLIPSCH, KEF, etc.).
Ces selfs à noyaux permettent surtout d'obtenir une valeur d'inductance plus pure, car non pervertis par la résistance du conducteur, en nécessitant moins de longueurs de câble.
- La première conséquence est la possibilité de filtrages plus efficaces.
- La deuxième conséquence est la possibilité d'utiliser des conducteurs de moindre section, ce dont nous connaissons l'influence bénéfique, de par notre métier, tout en conservant une résistance moindre.
Cette faible résistance en série d'une self de grave procurera un parfait amortissement du haut-parleur et par conséquent de magnifiques graves biens définis.
Le rendement sera aussi amélioréPour ma part, sur la "JCT Héritage", je n'utilise que des selfs à noyaux en ferrite avec du fil de 1,4mm en dessous de 150 Hz, pour une résistance totale de 0,2 ohms.
Pour les selfs de moyenne fréquence, le diamètre est de 0,8mm (maxi) pour une résistance inférieure à 0,5 ohms.
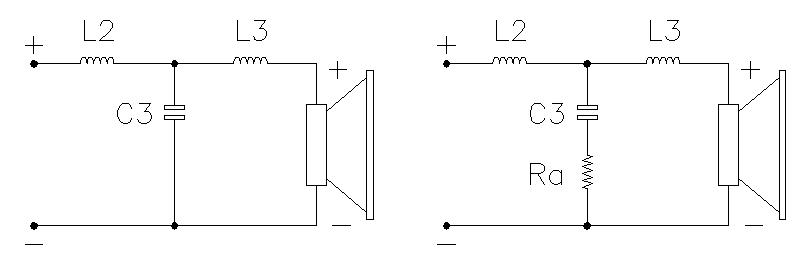
Ces selfs à Q élevé, utilisées en conjonction avec des condensateurs de haute qualité, peuvent créer des surtensions qu'il est toutefois facile d'amortir par une résistance ajustée, placée en série sur le composant relié à la masse.
Cette configuration vous permet de conserver le minimum de résistance en série avec le transducteur.
Pour exemple, si vous réalisez une cellule de grave pour le haut-parleur basse, vous placerez la self en série sur le haut-parleur et vous amortirez le condensateur à la masse (si c'est nécessaire) par une faible résistance en série ajustée pour amortir la surtension.Encore bravo pour l'intérêt de votre site.
Jean-Claude TORNIOR
À gauche, sans la résistance d'amortissement, à droite avec la résistance Ra (sous C3) d'amortissement de la surtension de la self.

Visualiser, et calculer le filtre passif à 18 dB :
Certain filtres demandent une correction des fréquences de coupure et un délais.
Les corrections, si elles sont nécessaires, vous seront proposées chapitre suivant.
Les valeurs proposées dans ce chapitre participent aux calculs des valeurs corrigées.
Un exemple :
Si un filtre demande un délais de 96 mm, et que vous entrez un délais de 2 mm dans ce chapitre, le calcul sera fait avec un délais de 96 + 2 = 98 mm.
Si vous entrez -2 mm dans ce chapitre, le calcul sera fait avec 96 - 2 = 94 mm.
La méthode est rigoureusement la même pour les fréquences de coupure, l'outil de calcul est fait pour vous simplifier le plus possible les choses.Les meilleurs résultats à l'écoute sont obtenus avec une mise en phase par recul du tweeter.
Le délais, s'il est nécessaire, vous sera proposé page suivante.
Si vous choisissez "Sans recul du tweeter", le calcul page suivante ajoutera un délais de mm sur le grave, et mettra le délais du tweeter à 0 mm.
Le délais du grave est modifiable ci-dessous dans le champs "Délais ou recul théorique du grave".
Vous verrez le résultat de ce choix sur la courbe de réponse.
Certain filtres sont très sensible, d'autres moins.Fréquence de coupure minimale du tweeter supérieure à 21 * Fs.
Ce sera la valeur proposée par défaut, si vous pensiez couper plus bas.
Si vous n'êtes pas un expert ne coupez pas plus bas, choisissez plutôt un autre tweeter.
18 dB Butterworth standard :
Avec 6 composants, le calcul est compliqué.
Sauf quand on a remarqué qu'il y avait un rapport précis entre les trois selfs et les trois capas de ce filtre :
- C1 = 1/3 * C2.
- C3 = 2/3 * C2.
- L3 = 1/3 * L2.
- L1 = 1/2 * L2.
Le calcul devient aussi simple qu'un filtre à 6 dB/octave pour les deux composants principaux.
Les autres composants sont calculés à partir des premiers.
Attention cette règle n'est vraie que si :
- Les impédances de la partie passe bas et passe haut sont identiques.
- Le filtre a une fonction de filtrage pur, sans faire la moindre correction de courbe de réponse.
En pratique, les impédances ne sont jamais totalement égales, et le filtre fait presque toujours une correction de courbe de réponse.
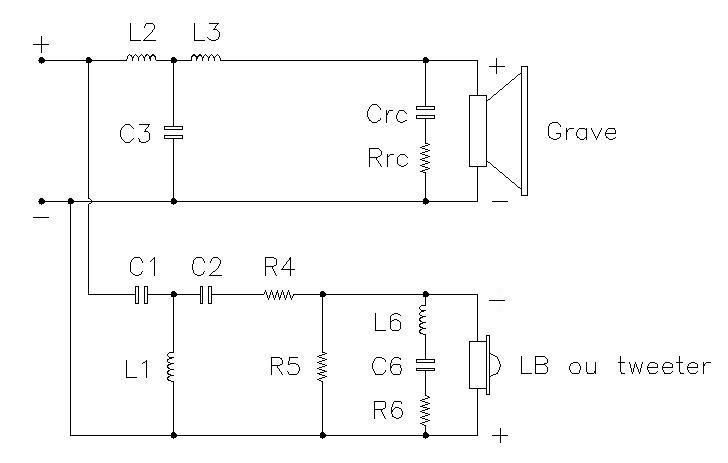
Passe haut, C2 :
La formule qui lie la fréquence de coupure F0 ou la pulsation w0 = 2 * PI * F0,
l'impédance du haut-parleur Z et la valeur du condensateur de filtrage C est :C2 = 2 / ( Z * W0 ). ( Si vous ajoutez R6, C6 et L6, prenez Z = R6 ).
C2 = 2 / ( Z * 2 * PI * F0 ) <==> C2 = 1 / ( Z * PI * F0 ) <==> C2 = 1 / Z / PI / F0
Unité : C2 en Farad, Z en Ohms et F0 en Hertz.
Si nous voulons C directement en uF, la formule devient :
C2 = 1000000 / ( Z * PI * F0 ) <==> C2 = 318310 / ( Z * F0 ) <==> C2 = 318310 / Z / F0Application numérique avec F0 = 1000 Hz et Z = 8 ohms, C2 = 318310 / 8 / 1000 = 39.8 uF
Passe bas, L2 :
La formule qui lie la fréquence de coupure F0 ou la pulsation w0 = 2 * PI * F0,
l'impédance du haut-parleur Z et la valeur de la self de filtrage L est :L2 = 3 * Z / ( 2 * w0 ). ( Je vous recommande d'ajouter Rrc et Crc, prenez Z = Rrc ).
L2 = 3 * Z / ( 2 * 2 * PI * F0 ) <==> L2 = 3 * Z / ( 4 * PI * F0 ) <==> L2 = 3 * Z / 4 / PI / F0
Unité : L en Henri, Z en Ohms et F en Hertz.
Si nous voulons L directement en mH, la formule devient :
L2 = 1000 * 3 * Z / ( 4 * PI * F0 ) <==> L2 = 1000 * 3 / ( 4 * PI ) * Z / F0 <==> L2 = 238.73 * Z / F0Application numérique avec F0 = 1000 Hz et Z = 8 ohms, L2 = 238.73 * 8 / 1000 = 1.9 mH
C1, C3, L1, L3 :
Les autres valeurs C1, C3, L1 et L3 sont obtenues par multiplication avec le coefficient indiqué si les impédances sont égales pour le passe haut et le passe bas.
18 dB Butterworth avec raccord à -5 dB :
D'après la méthode de Jean Michel LE CLEAC'H.Télécharger son fichier de calcul et ses explications.
Ce filtre se calcule exactement avec les même équations qu'un filtre Butterworth à 18 dB standard.
La méthode consiste en un décalage des fréquences de coupure du passe-haut et du passe-bas pour avoir une coupure à presque -5 dB au lieu de -3 dB.
Le décalage en profondeur du passe-haut se calcule simplement : ( 0.873 = 1 / 1.146 )
Sur un exemple de coupure à 1000 Hz.
18 dB standard 18 dB raccord à -5 dB Fréquence passe-bas 1000 Hz 0.8729 * 1000 = 873 Hz Fréquence passe-haut 1000 Hz 1.1456 * 1000 = 1146 Hz Décalage du passe haut à l'écoute 0.22 * 343707 / 1000 = 75.6 mm Il y a toujours un rapport théorique de 3 entre L2 et L3 et entre C2 et C1.
Par contre C3 et L1 doivent être calculés avec le formulaire au début de ce chapitre.C3 = C2 * 2/3 * 1.1462 = C2 * 0.876
L1 = L2 * 0.5 * 0.8732 = L2 * 0.381
Attention cette règle n'est vraie que si :
- Les impédances de la partie passe bas et passe haut sont identiques.
- Le filtre a une fonction de filtrage pur, sans faire la moindre correction de courbe de réponse.
En pratique, les impédances ne sont jamais totalement égales, et le filtre fait presque toujours une correction de courbe de réponse.
J'ai essayé ce filtre en actif en comparaison à un 18 dB Butterworth standard, ou un 24 dB Linkwitz Riley, et j'ai conservé ce filtre.
C'est aussi le filtre le plus recommandé pour raccorder un grave de grand diamètre à une compression de médium aigu avec pavillon :
Le décalage nécessaire du passe haut est réalisé mécaniquement par le fait que le pavillon est assez long, et que le point d'émission du couple pavillon / chambre de compression est plus reculé que celui du haut-parleur de grave.
De la théorie à la pratique :
Quand on fait une mise au point à l'écoute d'un filtre à 18 dB, il y a des écarts avec le calcul théorique.
L'une des causes de ces écarts est l'impédance qui n'est pas connue avec précision.
Une autre cause est la nécessité d'intégrer dans le filtre de coupure des corrections de courbes de réponses.
Il y a enfin la coupure naturelle du haut-parleur, qui, si elle est trop près de la coupure électrique, perturbe fortement la théorie.Par exemple, pour un filtre de coupure vers 1400 Hz entre un 38 cm et une compression 1 1/4 pouce, la théories dit qu'il faut prendre des selfs de 1.5 mH et 0.5 mH.
La pratique c'est 1.5 mH et 0.4 mH. La capa en parallèle fait 22 uF.
Pour ce même filtre, les capas sur la compression font 6.9 uF et 19.7 uF. La self en parallèle fait 0.68 uF.
Ce ne sont plus des valeurs de calculs.
L'écart n'est pas énorme, mais il est sensible à l'écoute.Le calcul est une aide pour acheter les composants.
Mais il faut intégrer qu'il faut aussi acheter les composants de valeurs proches pour les essayer à l'écoute, et les conserver si l'écoute le confirme.
Vouloir faire un filtre, sans avoir des composants en plus pour les essais, est une cause assurée d'échec.
Et si ce chapitre filtre à 18 dB est plus argumenté que celui à 12 dB, c'est que toutes tentatives de faire évoluer un filtre du 18 dB vers le 12 dB est moins bon à l'écoute.Le branchement théorique est avec un HP en opposition de phase par rapport à l'autre.
J'ai faits des branchements en phase, et d'autres en opposition de phase, après avoir mesuré le résultat pratique.
La théorie des filtre utilisée ici assimile les HP a des résistances pures, la pratique est bien différente, Les limites des calculs des filtres passifs.
Filtre à 18 dB dans les simulations numériques :
Dada du forum AUDAX (aujourd'hui le forum n'existe plus).
Le module de la fonction de transfert d'un filtre de type Butterworth répond a cette relation :
Passe bas : IHI = 1 / racine( 1 + ( F / Fo )2n )
Passe haut : IHI = ( Fo / F )n / racine( 1 + ( Fo / F )2n )
n est l'ordre du filtre et Fo la fréquence de coupure a -3 dB.
1 pour un filtre à 6 dB
2 pour un filtre à 12 dB
3 pour un filtre à 18 dB
4 pour un filtre à 24 dB
8 pour un filtre à 48 dB
ect...
L'atténuation en dB est alors donne par G = 20 x LOG( IHI )
Bruno du forum AUDAX :
Un filtre d'ordre 3 est la mise en cascade d'un filtre d'ordre 2 (avec le bon coefficient Q) et un filtre d'ordre 1.
Vous multipliez les fonctions de transfert.
- PASSE BAS : IHI = ( 1 / racine( 1 + ( F / F0 )2 ) ) * ( 1 / racine( ( 1 - ( F / F0 )2 )2 + (2 * zeta * F / F0 )2 ) )
- PASSE-HAUT : IHI = ( ( F / F0 ) / racine( 1 + ( F / F0 )2 ) ) * ( ( F / F0 )2 / racine( ( 1 - ( F / F0 )2 )2 + ( 2 * zeta * F / F0 )2 ) )
Avec zeta = 0.500
L'atténuation en dB est alors donne par G = 20 x LOG( IHI )
Un grand merci pour votre visite. --- Retour direct en haut de la page ---

Un grand-père facétieux disait à ses petits enfants que le grand truc blanc tout en haut du Puy-de-Dôme était un thermomètre géant : Quand il deviendra tout rouge il faudra vite se sauver, parce que le volcan va se réveiller !!!
Dôme Acoustique
Contrôle de validation W3C du code HTML 5 de la page, copiez l'adresse de la page avant de cliquer sur le lien.
Contrôle de validation W3C des CSS de la page, copiez l'adresse de la page avant de cliquer sur le lien.
Ce sont deux outils de contrôle pour le webmaster du site Dôme Acoustique, c'est inutile pour les utilisateurs.
Avoir le lien dans chaque page est plus simple pour les retrouver.